Horje
Print all Hamiltonian Cycles in an Undirected Graph

Given an undirected Graph consisting of N nodes in the form of an adjacency matrix graph[][] of size N*N, the task is to print all Hamiltonian cycles possible in the given undirected Graph (taking starting vertex as ‘0’).

A Hamiltonian cycle (or Hamiltonian circuit) is a Hamiltonian Path such that there is an edge (in the graph) from the last vertex to the first vertex of the Hamiltonian Path.

Examples:

Input: graph[][] = {{0, 1, 1, 0, 0, 1}, {1, 0, 1, 0, 1, 1}, {1, 1, 0, 1, 0, 0}, {0, 0, 1, 0, 1, 0}, {0, 1, 0, 1, 0, 1}, {1, 1, 0, 0, 1, 0}}
Output: 
0 1 2 3 4 5 0 
0 1 5 4 3 2 0 
0 2 3 4 1 5 0 
0 2 3 4 5 1 0 
0 5 1 4 3 2 0 
0 5 4 3 2 1 0 
Explanation:
All Possible Hamiltonian Cycles for the following graph (with the starting vertex as 0) are 

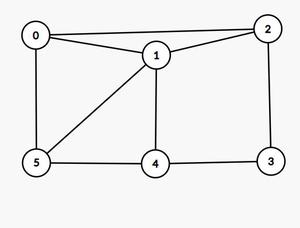
  1. {0 ? 1 ? 2 ? 3 ? 4 ? 5 ? 0}
  2. {0 ? 1 ? 5 ? 4 ? 3 ? 2 ? 0}
  3. {0 ? 2 ? 3 ? 4 ? 1 ? 5 ? 0}
  4. {0 ? 2 ? 3 ? 4 ? 5 ? 1 ? 0}
  5. {0 ? 5 ? 1 ? 4 ? 3 ? 2 ? 0}
  6. {0 ? 5 ? 4 ? 3 ? 2 ? 1 ? 0}

Input: graph[][] = {{0, 1, 0, 1, 1, 0, 0}, {1, 0, 1, 0, 0, 0, 0}, {0, 1, 0, 1, 0, 0, 1}, {1, 0, 1, 0, 0, 1, 0}, {1, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 1, 1, 0, 1}, {0, 0, 1, 0, 0, 1, 0}}
Output: No Hamiltonian Cycle possible
Explanation:
For the given graph, no Hamiltonian Cycle is possible: 

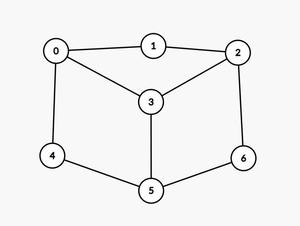
Approach: The given problem can be solved by using Backtracking to generate all possible Hamiltonian Cycles. Follow the steps below to solve the problem:

  • Create an auxiliary array, say path[] to store the order of traversal of nodes and a boolean array visited[] to keep track of vertices included in the current path.
  • Initially, add the source vertex (in this case ‘0’) to the path.
  • Now, recursively add vertices to path one by one to find the cycle.
  • Before adding a vertex to path, check whether the vertex being considered is adjacent to the previously added vertex or not and is not already in path. If such a vertex is found, then add it to the path and mark its value as true in the visited[] array.
  • If the length of path becomes equal to N, and there is an edge from the last vertex in path to 0, then print the path array.
  • After completing the above steps, if there exists no such path, then print No Hamiltonian Cycle possible.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include<bits/stdc++.h>
using namespace std;
 
// To check if there exists
// at least 1 hamiltonian cycle
bool hasCycle;
 
// Function to check if a vertex v
// can be added at index pos in
// the Hamiltonian Cycle
bool isSafe(int v, int graph[][6], vector<int> path, int pos)
{
   
    // If the vertex is adjacent to
    // the vertex of the previously
    // added vertex
    if (graph[path[pos - 1]][v] == 0)
        return false;
 
    // If the vertex has already
    // been included in the path
    for (int i = 0; i < pos; i++)
        if (path[i] == v)
            return false;
 
    // Both the above conditions are
    // not true, return true
    return true;
}
 
// Recursive function to find all
// hamiltonian cycles
void FindHamCycle(int graph[][6], int pos, vector<int> path, bool visited[], int N)
{
    // If all vertices are included
    // in Hamiltonian Cycle
    if (pos == N) {
 
        // If there is an edge
        // from the last vertex to
        // the source vertex
        if (graph[path[path.size() - 1]][path[0]] != 0) {
 
            // Include source vertex
            // into the path and
            // print the path
            path.push_back(0);
            for (int i = 0; i < path.size(); i++) {
                cout << path[i] << " ";
            }
            cout << endl;
 
            // Remove the source
            // vertex added
            path.pop_back();
 
            // Update the hasCycle
            // as true
            hasCycle = true;
        }
        return;
    }
 
    // Try different vertices
    // as the next vertex
    for (int v = 0; v < N; v++) {
 
        // Check if this vertex can
        // be added to Cycle
        if (isSafe(v, graph, path, pos) && !visited[v]) {
 
            path.push_back(v);
            visited[v] = true;
 
            // Recur to construct
            // rest of the path
            FindHamCycle(graph, pos + 1, path, visited, N);
 
            // Remove current vertex
            // from path and process
            // other vertices
            visited[v] = false;
            path.pop_back();
        }
    }
}
 
// Function to find all possible
// hamiltonian cycles
void hamCycle(int graph[][6], int N)
{
    // Initially value of boolean
    // flag is false
    hasCycle = false;
 
    // Store the resultant path
    vector<int> path;
    path.push_back(0);
 
    // Keeps the track of the
    // visited vertices
    bool visited[N];
 
    for (int i = 0; i < N; i++)
        visited[i] = false;
 
    visited[0] = true;
 
    // Function call to find all
    // hamiltonian cycles
    FindHamCycle(graph, 1, path, visited, N);
 
    if (!hasCycle) {
 
        // If no Hamiltonian Cycle
        // is possible for the
        // given graph
        cout << "No Hamiltonian Cycle" << "possible " << endl;
        return;
    }
}
     
int main()
{
    int graph[][6] = {
            { 0, 1, 1, 0, 0, 1 },
            { 1, 0, 1, 0, 1, 1 },
            { 1, 1, 0, 1, 0, 0 },
            { 0, 0, 1, 0, 1, 0 },
            { 0, 1, 0, 1, 0, 1 },
            { 1, 1, 0, 0, 1, 0 },
        };
    hamCycle(graph, 6);
 
    return 0;
}
 
// This code is contributed by rameshtravel07.

Java

// Java program for the above approach
 
import java.util.ArrayList;
class GFG {
 
    // Function to check if a vertex v
    // can be added at index pos in
    // the Hamiltonian Cycle
    boolean isSafe(int v, int graph[][],
                   ArrayList<Integer> path,
                   int pos)
    {
        // If the vertex is adjacent to
        // the vertex of the previously
        // added vertex
        if (graph[path.get(pos - 1)][v]
            == 0)
            return false;
 
        // If the vertex has already
        // been included in the path
        for (int i = 0; i < pos; i++)
            if (path.get(i) == v)
                return false;
 
        // Both the above conditions are
        // not true, return true
        return true;
    }
 
    // To check if there exists
    // at least 1 hamiltonian cycle
    boolean hasCycle;
 
    // Function to find all possible
    // hamiltonian cycles
    void hamCycle(int graph[][])
    {
        // Initially value of boolean
        // flag is false
        hasCycle = false;
 
        // Store the resultant path
        ArrayList<Integer> path
            = new ArrayList<>();
        path.add(0);
 
        // Keeps the track of the
        // visited vertices
        boolean[] visited
            = new boolean[graph.length];
 
        for (int i = 0;
             i < visited.length; i++)
            visited[i] = false;
 
        visited[0] = true;
 
        // Function call to find all
        // hamiltonian cycles
        FindHamCycle(graph, 1, path,
                     visited);
 
        if (!hasCycle) {
 
            // If no Hamiltonian Cycle
            // is possible for the
            // given graph
            System.out.println(
                "No Hamiltonian Cycle"
                + "possible ");
            return;
        }
    }
 
    // Recursive function to find all
    // hamiltonian cycles
    void FindHamCycle(int graph[][], int pos,
                      ArrayList<Integer> path,
                      boolean[] visited)
    {
        // If all vertices are included
        // in Hamiltonian Cycle
        if (pos == graph.length) {
 
            // If there is an edge
            // from the last vertex to
            // the source vertex
            if (graph[path.get(path.size() - 1)]
                     [path.get(0)]
                != 0) {
 
                // Include source vertex
                // into the path and
                // print the path
                path.add(0);
                for (int i = 0;
                     i < path.size(); i++) {
                    System.out.print(
                        path.get(i) + " ");
                }
                System.out.println();
 
                // Remove the source
                // vertex added
                path.remove(path.size() - 1);
 
                // Update the hasCycle
                // as true
                hasCycle = true;
            }
            return;
        }
 
        // Try different vertices
        // as the next vertex
        for (int v = 0;
             v < graph.length; v++) {
 
            // Check if this vertex can
            // be added to Cycle
            if (isSafe(v, graph, path, pos)
                && !visited[v]) {
 
                path.add(v);
                visited[v] = true;
 
                // Recur to construct
                // rest of the path
                FindHamCycle(
                    graph, pos + 1,
                    path, visited);
 
                // Remove current vertex
                // from path and process
                // other vertices
                visited[v] = false;
                path.remove(
                    path.size() - 1);
            }
        }
    }
 
    // Driver Code
    public static void main(String args[])
    {
        GFG hamiltonian = new GFG();
 
        /* Input Graph:
           (0) - - -- (2)
            |   \   /  |
            |    (1)   |
            |   /  |   |
            | /    |   |
           (5)----(4)--(3)*/
 
        int[][] graph = {
            { 0, 1, 1, 0, 0, 1 },
            { 1, 0, 1, 0, 1, 1 },
            { 1, 1, 0, 1, 0, 0 },
            { 0, 0, 1, 0, 1, 0 },
            { 0, 1, 0, 1, 0, 1 },
            { 1, 1, 0, 0, 1, 0 },
        };
        hamiltonian.hamCycle(graph);
    }
}

Python3

# Python3 program for the above approach
 
# Function to check if a vertex v
# can be added at index pos in
# the Hamiltonian Cycle
def isSafe(v, graph, path, pos):
   
    # If the vertex is adjacent to
    # the vertex of the previously
    # added vertex
    if graph[path[pos - 1]][v] == 0:
        return False
 
    # If the vertex has already
    # been included in the path
    for i in range(pos):
        if path[i] == v:
            return False
 
    # Both the above conditions are
    # not true, return true
    return True
 
# To check if there exists
# at least 1 hamiltonian cycle
hasCycle = False
 
# Function to find all possible
# hamiltonian cycles
def hamCycle(graph):
    global hasCycle
     
    # Initially value of boolean
    # flag is false
    hasCycle = False
 
    # Store the resultant path
    path = []
    path.append(0)
 
    # Keeps the track of the
    # visited vertices
    visited = [False]*(len(graph))
 
    for i in range(len(visited)):
        visited[i] = False
 
    visited[0] = True
 
    # Function call to find all
    # hamiltonian cycles
    FindHamCycle(graph, 1, path, visited)
 
    if hasCycle:
        # If no Hamiltonian Cycle
        # is possible for the
        # given graph
        print("No Hamiltonian Cycle" + "possible ")
        return
 
# Recursive function to find all
# hamiltonian cycles
def FindHamCycle(graph, pos, path, visited):
   
    # If all vertices are included
    # in Hamiltonian Cycle
    if pos == len(graph):
       
        # If there is an edge
        # from the last vertex to
        # the source vertex
        if graph[path[-1]][path[0]] != 0:
           
            # Include source vertex
            # into the path and
            # print the path
            path.append(0)
            for i in range(len(path)):
                print(path[i], end = " ")
            print()
 
            # Remove the source
            # vertex added
            path.pop()
 
            # Update the hasCycle
            # as true
            hasCycle = True
        return
 
    # Try different vertices
    # as the next vertex
    for v in range(len(graph)):
       
        # Check if this vertex can
        # be added to Cycle
        if isSafe(v, graph, path, pos) and not visited[v]:
            path.append(v)
            visited[v] = True
 
            # Recur to construct
            # rest of the path
            FindHamCycle(graph, pos + 1, path, visited)
 
            # Remove current vertex
            # from path and process
            # other vertices
            visited[v] = False
            path.pop()
 
""" Input Graph:
   (0) - - -- (2)
    |   \   /  |
    |    (1)   |
    |   /  |   |
    | /    |   |
   (5)----(4)--(3)"""
 
graph = [
    [ 0, 1, 1, 0, 0, 1 ],
    [ 1, 0, 1, 0, 1, 1 ],
    [ 1, 1, 0, 1, 0, 0 ],
    [ 0, 0, 1, 0, 1, 0 ],
    [ 0, 1, 0, 1, 0, 1 ],
    [ 1, 1, 0, 0, 1, 0 ],
]
hamCycle(graph)
 
# This code is contributed by divyesh072019.

C#

// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG {
     
    // Function to check if a vertex v
    // can be added at index pos in
    // the Hamiltonian Cycle
    static bool isSafe(int v, int[,] graph, List<int> path, int pos)
    {
        // If the vertex is adjacent to
        // the vertex of the previously
        // added vertex
        if (graph[path[pos - 1],v] == 0)
            return false;
   
        // If the vertex has already
        // been included in the path
        for (int i = 0; i < pos; i++)
            if (path[i] == v)
                return false;
   
        // Both the above conditions are
        // not true, return true
        return true;
    }
   
    // To check if there exists
    // at least 1 hamiltonian cycle
    static bool hasCycle;
   
    // Function to find all possible
    // hamiltonian cycles
    static void hamCycle(int[,] graph)
    {
        // Initially value of boolean
        // flag is false
        hasCycle = false;
   
        // Store the resultant path
        List<int> path = new List<int>();
        path.Add(0);
   
        // Keeps the track of the
        // visited vertices
        bool[] visited = new bool[graph.GetLength(0)];
   
        for (int i = 0; i < visited.Length; i++)
            visited[i] = false;
   
        visited[0] = true;
   
        // Function call to find all
        // hamiltonian cycles
        FindHamCycle(graph, 1, path, visited);
   
        if (!hasCycle) {
   
            // If no Hamiltonian Cycle
            // is possible for the
            // given graph
            Console.WriteLine("No Hamiltonian Cycle" + "possible ");
            return;
        }
    }
   
    // Recursive function to find all
    // hamiltonian cycles
    static void FindHamCycle(int[,] graph, int pos, List<int> path, bool[] visited)
    {
        // If all vertices are included
        // in Hamiltonian Cycle
        if (pos == graph.GetLength(0)) {
   
            // If there is an edge
            // from the last vertex to
            // the source vertex
            if (graph[path[path.Count - 1], path[0]] != 0) {
   
                // Include source vertex
                // into the path and
                // print the path
                path.Add(0);
                for (int i = 0; i < path.Count; i++) {
                    Console.Write(path[i] + " ");
                }
                Console.WriteLine();
   
                // Remove the source
                // vertex added
                path.RemoveAt(path.Count - 1);
   
                // Update the hasCycle
                // as true
                hasCycle = true;
            }
            return;
        }
   
        // Try different vertices
        // as the next vertex
        for (int v = 0; v < graph.GetLength(0); v++) {
   
            // Check if this vertex can
            // be added to Cycle
            if (isSafe(v, graph, path, pos) && !visited[v]) {
   
                path.Add(v);
                visited[v] = true;
   
                // Recur to construct
                // rest of the path
                FindHamCycle(graph, pos + 1, path, visited);
   
                // Remove current vertex
                // from path and process
                // other vertices
                visited[v] = false;
                path.RemoveAt(path.Count - 1);
            }
        }
    }
 
  static void Main() {
      /* Input Graph:
       (0) - - -- (2)
        |   \   /  |
        |    (1)   |
        |   /  |   |
        | /    |   |
       (5)----(4)--(3)*/
 
    int[,] graph = {
        { 0, 1, 1, 0, 0, 1 },
        { 1, 0, 1, 0, 1, 1 },
        { 1, 1, 0, 1, 0, 0 },
        { 0, 0, 1, 0, 1, 0 },
        { 0, 1, 0, 1, 0, 1 },
        { 1, 1, 0, 0, 1, 0 },
    };
    hamCycle(graph);
  }
}
 
// This code is contributed by suresh07.

Javascript

<script>
    // Javascript program for the above approach
     
    // Function to check if a vertex v
    // can be added at index pos in
    // the Hamiltonian Cycle
    function isSafe(v, graph, path, pos)
    {
     
        // If the vertex is adjacent to
        // the vertex of the previously
        // added vertex
        if (graph[path[pos - 1]][v] == 0)
            return false;
    
        // If the vertex has already
        // been included in the path
        for (let i = 0; i < pos; i++)
            if (path[i] == v)
                return false;
    
        // Both the above conditions are
        // not true, return true
        return true;
    }
    
    // To check if there exists
    // at least 1 hamiltonian cycle
    let hasCycle;
    
    // Function to find all possible
    // hamiltonian cycles
    function hamCycle(graph)
    {
        // Initially value of boolean
        // flag is false
        hasCycle = false;
    
        // Store the resultant path
        let path = [];
        path.push(0);
    
        // Keeps the track of the
        // visited vertices
        let visited = new Array(graph.length);
    
        for (let i = 0; i < visited.length; i++)
            visited[i] = false;
    
        visited[0] = true;
    
        // Function call to find all
        // hamiltonian cycles
        FindHamCycle(graph, 1, path, visited);
    
        if (!hasCycle) {
    
            // If no Hamiltonian Cycle
            // is possible for the
            // given graph
            document.write("No Hamiltonian Cycle" + "possible ");
            return;
        }
    }
    
    // Recursive function to find all
    // hamiltonian cycles
    function FindHamCycle(graph, pos, path, visited)
    {
        // If all vertices are included
        // in Hamiltonian Cycle
        if (pos == graph.length) {
    
            // If there is an edge
            // from the last vertex to
            // the source vertex
            if (graph[path[path.length - 1]][path[0]] != 0) {
    
                // Include source vertex
                // into the path and
                // print the path
                path.push(0);
                for (let i = 0; i < path.length; i++) {
                    document.write(path[i] + " ");
                }
                document.write("</br>");
    
                // Remove the source
                // vertex added
                path.pop();
    
                // Update the hasCycle
                // as true
                hasCycle = true;
            }
            return;
        }
    
        // Try different vertices
        // as the next vertex
        for (let v = 0; v < graph.length; v++) {
    
            // Check if this vertex can
            // be added to Cycle
            if (isSafe(v, graph, path, pos) && !visited[v]) {
    
                path.push(v);
                visited[v] = true;
    
                // Recur to construct
                // rest of the path
                FindHamCycle(graph, pos + 1, path, visited);
    
                // Remove current vertex
                // from path and process
                // other vertices
                visited[v] = false;
                path.pop();
            }
        }
    }
     
    /* Input Graph:
       (0) - - -- (2)
        |   \   /  |
        |    (1)   |
        |   /  |   |
        | /    |   |
       (5)----(4)--(3)*/
  
    let graph = [
        [ 0, 1, 1, 0, 0, 1 ],
        [ 1, 0, 1, 0, 1, 1 ],
        [ 1, 1, 0, 1, 0, 0 ],
        [ 0, 0, 1, 0, 1, 0 ],
        [ 0, 1, 0, 1, 0, 1 ],
        [ 1, 1, 0, 0, 1, 0 ],
    ];
    hamCycle(graph);
  
 // This code is contributed by divyeshrabadiya07.
</script>

Output: 

0 1 2 3 4 5 0 
0 1 5 4 3 2 0 
0 2 3 4 1 5 0 
0 2 3 4 5 1 0 
0 5 1 4 3 2 0 
0 5 4 3 2 1 0

 

Time Complexity: O(N!)
Auxiliary Space: O(N)


 


Reffered: https://www.geeksforgeeks.org

Graph

Related
Minimize number of notes required to be distributed among students Minimize number of notes required to be distributed among students
Shortest path for a thief to reach the Nth house avoiding policemen Shortest path for a thief to reach the Nth house avoiding policemen
Maximum Bitwise XOR of node values of an Acyclic Graph made up of N given vertices using M edges Maximum Bitwise XOR of node values of an Acyclic Graph made up of N given vertices using M edges
Maximum cost path from source node to destination node via at most K intermediate nodes Maximum cost path from source node to destination node via at most K intermediate nodes
Java Program to Implement of Gabow Scaling Algorithm Java Program to Implement of Gabow Scaling Algorithm

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 12



 

Horje