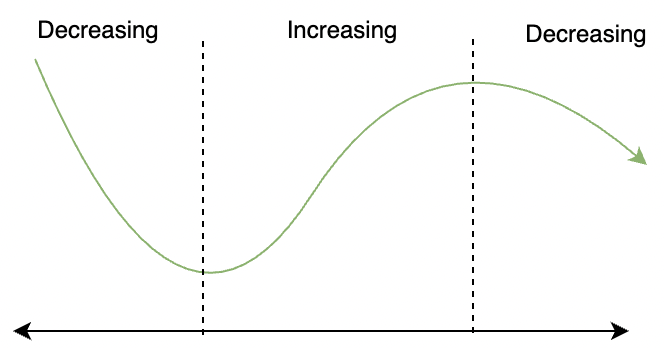
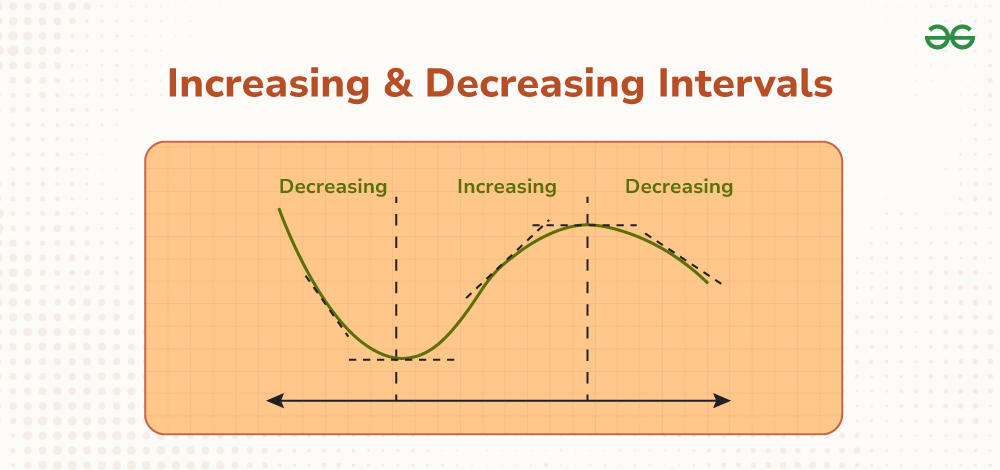
Increasing and decreasing intervals are the intervals of real numbers in which real-valued functions are increasing and decreasing respectively. The Derivatives are the way of measuring the rate of change of a variable.

Increasing and Decreasing Intervals

When it comes to functions and calculus, derivatives give us a lot of information about the function’s shape and its graph. They give information about the regions where the function is increasing or decreasing. Derivatives are also useful in finding out the maximum and minimum values attained by a function. A function’s graph when plotted through the information collected from derivatives can help us find out the limit and other information about the function’s behavior.

What is Increasing and Decreasing Interval

The interval of region will increase if the value of the function f(x) increases with an increase in the value of x and it will decrease if f(x) decreases with a decrease in x. This information can be used to find out the intervals or the regions where the function is increasing or decreasing.

Once such intervals are known, it is not very difficult to figure out the valleys and hills in the function’s graph. The figure below shows a function f(x) and its intervals where it increases and decreases.

For a function f(x). For an interval i defined in its domain. 

1. The function f(x) is said to be increasing in an interval I if for every a < b, f(a) ≤ f(b).
2. The function f(x) is said to be decreasing in an interval I if for every a < b, f(a) ≥ f(b).

The function is called strictly increasing if for every a < b, f(a) < f(b). Similar definition holds for strictly decreasing case. 

Increasing and Decreasing Intervals

The concept behind Increasing and Decreasing Intervals is to identify these areas without looking at the function’s graph. For this, let’s look at the derivatives of the function in these regions. The fact that these derivatives are nothing but the slope of tangents at this curve is already established. The figure below shows the slopes of the tangents at different points on this curve.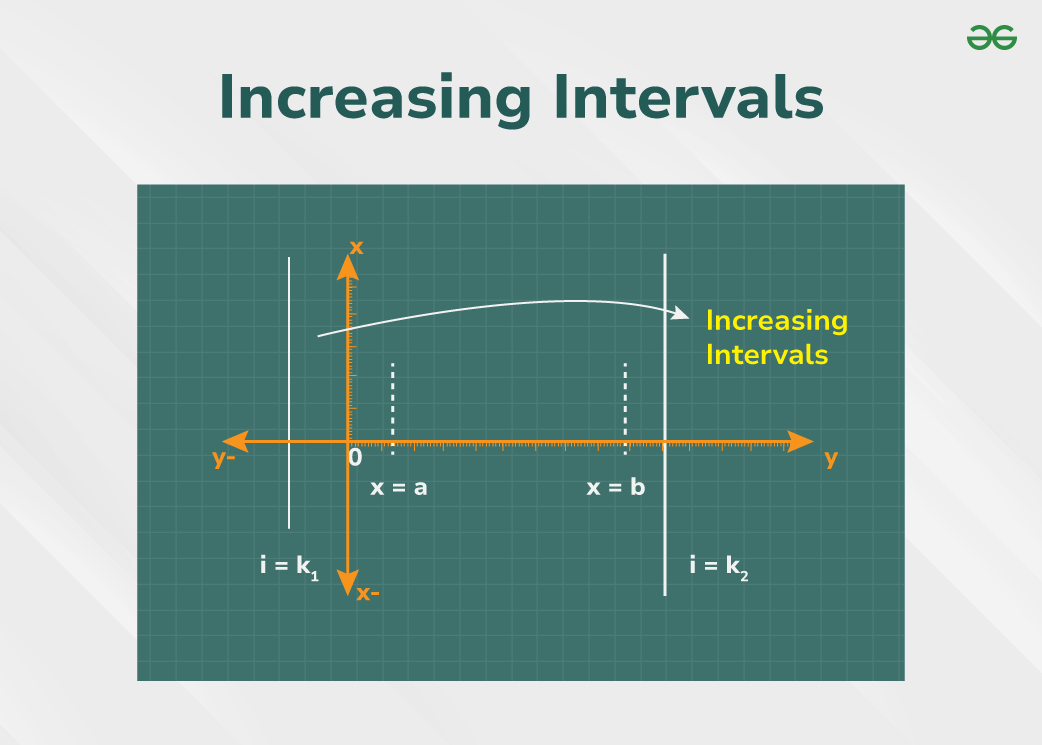 

Increasing Intervals

Decreasing Intervals

Notice that in the regions where the function is decreasing, the slope of curve is actually negative and positive for the regions where the function is increasing. The slope at peaks and valleys is zero. So, to say formally. 

Let’s say f(x) is a continuous function on [a, b] and differentiable in the interval (a, b). 

1. If f'(c) > 0 for all c in (a, b), then f(x) is said to be increasing in the interval.
2. If f'(c) < 0 for all c in (a, b), then f(x) is said to be decreasing in the interval.
3. If f'(c) = 0 for all c in (a, b), then f(x) is said to be constant in the interval.

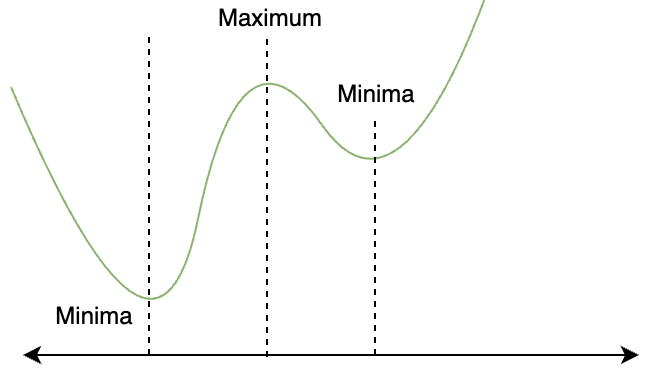
Must Read

• Continuity of Functions

Critical Point

Critical Point is a point where derivative of the function becomes zero. In the previous diagram notice how when the function goes from decreasing to increasing or from increasing to decreasing. There is a valley or a peak. These valleys and peaks are extreme points of the function, and thus they are called extrema.

>

It is pretty evident from the figure that at these points the derivative of the function becomes zero. The function attains its minimum and maximum values at these points. 

Note: A function can have any number of critical points. While all the critical points do not necessarily give maximum and minimum value of the function. But every critical point is valley that is a minimum point in local region. 

In the figure above, there are three extremes, two of them are minima, but there are only one global maximum and global minima. So in formal terms, 

For a function f(x), a point x = c is extrema if, 

f'(c) = 0

Identify Increasing and Decreasing Intervals

It becomes clear from the above figures that every extrema of the function is a point where its derivative changes sign. That is function either goes from increasing to decreasing or vice versa. While looking for regions where the function is increasing or decreasing, it becomes essential to look around the extremes. For any function f(x) and a given interval, the following steps need to be followed for finding out these intervals: 

1. Check if the function is differentiable and continuous in the given interval.
2. Solve the equation f'(x) = 0, solutions to this equations give us extremes.
3. For an extreme point x = c, look in the region in the vicinity of that point and check the signs of derivatives to find out the intervals where the function is increasing or decreasing.

Let’s look at some sample problems related to these concepts. 

Sample Problems on Increasing and Decreasing Intervals

Question 1: For the given function, tell whether it’s increasing or decreasing in the region [-1,1]

f(x) = e^x

Solution: 

To analyze any function, first step is to look for critical points. 

f(x) = e^x

f'(x) = e^x  …. (1) 

Solving the equation f'(x) = 0 

e^x = 0 

There is no critical point for this function in the given region. That means that in the given region, this function must be either monotonically increasing or monotonically decreasing. For that, check the derivative of the function in this region. 

f'(x) > 0 in the interval [0,1]. 

Thus, the function is increasing. 

Question 2: For the given function, tell whether it’s increasing or decreasing in the region [2,4]

f(x) = x² – x – 4

Solution: 

To analyze any function, first step is to look for critical points. 

f(x) = x² – x – 4

f'(x) = 2x – 1  …. (1) 

Solving the equation f'(x) = 0 

2x – 1 = 0 

⇒ x = 0.5

The critical point is outside the region of interest. That means that in the given region, this function must be either monotonically increasing or monotonically decreasing. For that, check the derivative of the function in this region. 

f'(x) > 0 in the interval [2,4]. 

Thus, the function is increasing. 

Question 3: Find the regions where the given function is increasing or decreasing. 

f(x) = 3x + 4

Solution: 

To analyze any function, first step is to look for critical points. 

f(x) = 3x + 4

f'(x) = 3 

This equation is not zero for any x. That means the derivative of this function is constant through it’s domain. 

Since f'(x) > 0 for all the values of x. 

The function is monotonically increasing over it’s domain. 

Question 4: Find the regions where the given function is increasing or decreasing. 

f(x) = x² + 4x + 4

Solution: 

To analyze any function, first step is to look for critical points. 

f(x) = x² + 4x + 4

f'(x) = 2x + 4 …. (1) 

Solving the equation f'(x) = 0 

2x + 4 = 0 

⇒ x = -2 

Thus, at x =-2 the derivative this function changes its sign. Check for the sign of derivative in its vicinity. 

at x = -1 

f'(x) = 2(-1) + 4 = 2 > 0 

This means for x > -2 the function is increasing. 

at x = -3 

f'(x) = 2(-3) + 4 = -2 < 0 

For x < -2, the function is decreasing. 

Question 5: Find the regions where the given function is increasing or decreasing. 

f(x) = x² + 3x

Solution: 

To analyze any function, first step is to look for critical points. 

f(x) = x² + 3x

f'(x) = 2x + 3 …. (1) 

Solving the equation f'(x) = 0 

2x + 3 = 0 

⇒ x = -1.5 

Thus, at x =-1.5 the derivative this function changes its sign. Check for the sign of derivative in its vicinity. 

at x = -1 

f'(x) = 2(-1) + 3 = 1 > 0 

This means for x > -1.5 the function is increasing. 

at x = -3 

f'(x) = 2(-3) + 3 = -3 < 0 

For x < -1.5, the function is decreasing. 

Question 6: Find the regions where the given function is increasing or decreasing. 

f(x) = e^x + e^-x

Solution: 

To analyze any function, first step is to look for critical points. 

f(x) = e^x + e^-x

f'(x) = e^x – e^-x …. (1) 

Solving the equation f'(x) = 0 

e^x – e^-x= 0 

⇒ e^x = e^-x

⇒ e^2x = 1

⇒ e^2x = e⁰

Comparing both sides of the equation, 

⇒2x = 0 

⇒x = 0

Thus, at x = 0 the derivative this function changes its sign. Check for the sign of derivative in its vicinity. 

at x = 1 

f'(x) = e¹ – e^-1 > 0 

This means for x > 0 the function is increasing. 

at x = –1 

f'(x) = e^-1 – e¹ < 0 

For x < 0, the function is decreasing.