Horje
Sort the array using slow sort

Given an array arr[] consisting of N integers, the task is to sort the given array in ascending order using the slow sort.

Examples:

Input: arr[] = {6, 8, 9, 4, 12, 1}
Output: 1 4 6 8 9 12

Input: arr[] = {5, 4, 3, 2, 1}
Output: 1 2 3 4 5

Approach: Like Merge Sort, Slow Sort is a Divide and Conquer algorithm. It divides the input array into two halves, calls itself the two halves, and then compares the maximum element of the two halves. It stores the maximum element of a sub-array at the top position of the sub-array, then, it recursively calls the sub-array without the maximum element. Follow the steps below to solve the problem:

SlowSort(arr[], l, r):

  • If r >= l, perform the following steps:
    • Find the middle value of the array as m = (l + r) / 2.
    • Recursively call function SlowSort to find the maximum of first half elements: SlowSort(arr, l, m)
    • Recursively call function SlowSort to find the maximum of second-half elements: SlowSort(arr, m + 1, r)
    • Store the largest of two maxima returned from the above function calls at the end as arr[r] = max(arr[m], arr[r])
    • Recursively call function SlowSort without the maximum obtained in the above step: SlowSort(arr, l, r-1)

The following figure shows the complete Slow Sort process. For example, array {9, 6, 8, 4, 1, 3, 7, 2}. From the figure, it can be observed that the array is recursively divided into two halves till the size becomes 1. Once the size becomes 1, the comparison process begins. 

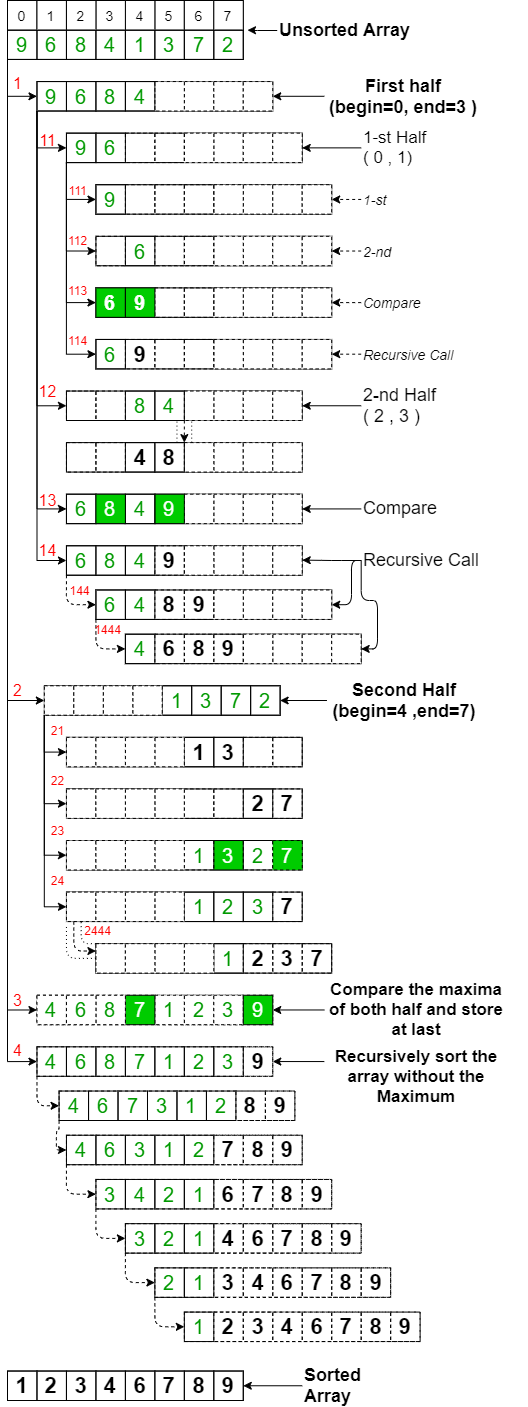Slow Sort

Slow Sort

Below is the implementation for the above approach: 

C++

// C++ program for the above approach
#include <iostream>
using namespace std;
 
// Function to swap two elements
void swap(int* xp, int* yp)
{
    int temp = *xp;
    *xp = *yp;
    *yp = temp;
}
 
// Function to sort the array using
// the Slow sort
void slow_sort(int A[], int i, int j)
{
    // Recursion break condition
    if (i >= j)
        return;
 
    // Store the middle value
    int m = (i + j) / 2;
 
    // Recursively call with the
    // left half
    slow_sort(A, i, m);
 
    // Recursively call with the
    // right half
    slow_sort(A, m + 1, j);
 
    // Swap if the first element is
    // lower than second
    if (A[j] < A[m]) {
        swap(&A[j], &A[m]);
    }
 
    // Recursively call with the
    // array excluding the maximum
    // element
    slow_sort(A, i, j - 1);
}
 
// Function to print the array
void printArray(int arr[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        cout << arr[i] << " ";
    cout << endl;
}
 
// Driver Code
int main()
{
    // Given Input
    int arr[] = { 6, 8, 9, 4, 12, 1 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    // Function Call
    slow_sort(arr, 0, n - 1);
 
    // Print the sorted array
    printArray(arr, n);
 
    return 0;
}

Java

// Java program for the above approach
class GFG{
 
// Function to sort the array using
// the Slow sort
static void slow_sort(int A[], int i, int j)
{
     
    // Recursion break condition
    if (i >= j)
        return;
 
    // Store the middle value
    int m = (i + j) / 2;
 
    // Recursively call with the
    // left half
    slow_sort(A, i, m);
 
    // Recursively call with the
    // right half
    slow_sort(A, m + 1, j);
 
    // Swap if the first element is
    // lower than second
    if (A[j] < A[m])
    {
        int temp = A[j];
        A[j] = A[m];
        A[m] = temp;
    }
 
    // Recursively call with the
    // array excluding the maximum
    // element
    slow_sort(A, i, j - 1);
}
 
// Function to print the array
static void printArray(int arr[], int size)
{
    int i;
    for(i = 0; i < size; i++)
        System.out.print(arr[i] + " ");
         
    System.out.println();
}
 
// Driver code
public static void main(String[] args)
{
    int arr[] = { 6, 8, 9, 4, 12, 1 };
    int n = arr.length;
 
    // Function Call
    slow_sort(arr, 0, n - 1);
 
    // Print the sorted array
    printArray(arr, n);
}
}
 
// This code is contributed by abhinavjain194

Python3

# Python3 program for the above approach
 
# Function to sort the array using
# the Slow sort
def slow_sort(A, i, j):
     
    # Recursion break condition
    if (i >= j):
        return
         
    # Store the middle value
    m = (i + j) // 2
     
    # Recursively call with the
    # left half
    slow_sort(A, i, m)
 
    # Recursively call with the
    # right half
    slow_sort(A, m + 1, j)
 
    # Swap if the first element is
    # lower than second
    if (A[j] < A[m]):
        temp = A[m]
        A[m] = A[j]
        A[j] = temp
 
    # Recursively call with the
    # array excluding the maximum
    # element
    slow_sort(A, i, j - 1)
 
# Function to print the array
def printArray(arr, size):
     
    for i in range(size):
        print(arr[i], end = " ")
 
# Driver Code
if __name__ == '__main__':
     
    arr = [ 6, 8, 9, 4, 12, 1 ]
    n = len(arr)
     
    # Function Call
    slow_sort(arr, 0, n - 1)
     
    # Print the sorted array
    printArray(arr, n)
 
# This code is contributed by SoumikMondal

C#

// C# implementation of the approach
using System;
 
class GFG
{
   
// Function to sort the array using
// the Slow sort
static void slow_sort(int[] A, int i, int j)
{
     
    // Recursion break condition
    if (i >= j)
        return;
 
    // Store the middle value
    int m = (i + j) / 2;
 
    // Recursively call with the
    // left half
    slow_sort(A, i, m);
 
    // Recursively call with the
    // right half
    slow_sort(A, m + 1, j);
 
    // Swap if the first element is
    // lower than second
    if (A[j] < A[m])
    {
        int temp = A[j];
        A[j] = A[m];
        A[m] = temp;
    }
 
    // Recursively call with the
    // array excluding the maximum
    // element
    slow_sort(A, i, j - 1);
}
 
// Function to print the array
static void printArray(int[] arr, int size)
{
    int i;
    for(i = 0; i < size; i++)
        Console.Write(arr[i] + " ");
         
    Console.WriteLine();
}
 
    // Driver code
    public static void Main()
    {
    int[] arr = { 6, 8, 9, 4, 12, 1 };
    int n = arr.Length;
 
    // Function Call
    slow_sort(arr, 0, n - 1);
 
    // Print the sorted array
    printArray(arr, n);
    }
}
 
// this code is contributed by sanjoy_62.

Javascript

<script>
 
    // JavaScript program for the above approach
     
    // Function to sort the array using
    // the Slow sort
    function slow_sort(A, i, j)
    {
 
        // Recursion break condition
        if (i >= j)
            return;
 
        // Store the middle value
        let m = parseInt((i + j) / 2, 10);
 
        // Recursively call with the
        // left half
        slow_sort(A, i, m);
 
        // Recursively call with the
        // right half
        slow_sort(A, m + 1, j);
 
        // Swap if the first element is
        // lower than second
        if (A[j] < A[m])
        {
            let temp = A[j];
            A[j] = A[m];
            A[m] = temp;
        }
 
        // Recursively call with the
        // array excluding the maximum
        // element
        slow_sort(A, i, j - 1);
    }
 
    // Function to print the array
    function printArray(arr, size)
    {
        let i;
        for(i = 0; i < size; i++)
            document.write(arr[i] + " ");
 
        document.write("</br>");
    }
     
    let arr = [ 6, 8, 9, 4, 12, 1 ];
    let n = arr.length;
  
    // Function Call
    slow_sort(arr, 0, n - 1);
  
    // Print the sorted array
    printArray(arr, n);
     
</script>

Output: 
1 4 6 8 9 12

 

Best Case Time Complexity: O(N^{\frac{log_2 N}{2 + e}}) , where e > 0
Average Case Time Complexity: O(N^{\frac{log_2 N}{2}})
Auxiliary Space: O(1)


 


Reffered: https://www.geeksforgeeks.org

Divide And Conquer

Related
Print all array elements appearing more than N / K times Print all array elements appearing more than N / K times
Minimum count of elements required to obtain the given Array by repeated mirror operations Minimum count of elements required to obtain the given Array by repeated mirror operations
Calculate weight of parenthesis based on the given conditions Calculate weight of parenthesis based on the given conditions
Divide N into K parts in the form (X, 2X, ... , KX) for some value of X Divide N into K parts in the form (X, 2X, ... , KX) for some value of X
Largest Square in a Binary Matrix with at most K 1s for multiple Queries Largest Square in a Binary Matrix with at most K 1s for multiple Queries

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 13



 

Horje