In a cricket match, before the game begins. Two captains go for a toss. Tossing is an activity of flipping a coin and checking the result as either “Head” or “Tail”. Similarly, tossing a die gives us a number from 1 to 6. All these activities are examples of experiments. An activity that gives us a result is called an experiment.

There can be more than one outcome of an experiment. The field of probability is more concerned with random experiments. These experiments do not have a definite outcome, that is you cannot predict the outcome of these experiments with absolute certainty. 

What is an Experiments?

Probability theory is based on experiments. An experiment is a test, trial, or procedure to discover something unknown, testing a principle or supposition, etc. Following is the list of some activities that can be considered as experiments: 

1. Toss the coin repeatedly and note the outcomes. There are two possible outcomes – Head(H) or Tails(T).
2. Throwing a fair die and observing the number it gives as a result.
3. Driving from Delhi to Bangalore and measuring the distance between the two cities.

All the activities listed above can be described as experiments. Notice that in Activity 1 and Activity 2, we do not know the result of the activity and cannot say with certainty what number will appear on-die or whether we will get a head or tails with the coin toss. The result of activity 3 can be predicted easily. This means that there is randomness involved in experiments 1 and 2. Such experiments are called random experiments. 

Random Experiments

The underlying assumption of the probability theory is that the experiments must be random. It is assumed that the experiment can be performed infinitely many times under the same conditions. This assumption becomes important because both classical probability theory and frequency-based probability theory rely on this assumption as they look for long-term behaviours in the experiments. 

A random experiment is defined as an experiment whose outcome cannot be predicted with certainty.

It is impossible to predict the result when a die is rolled. This is an example of a random experiment. Each random experiment must fulfil the following two conditions: 

• Experiment can be repeated a number of times under the same conditions.
• Outcome of the experiment cannot be predicted beforehand with certainty.

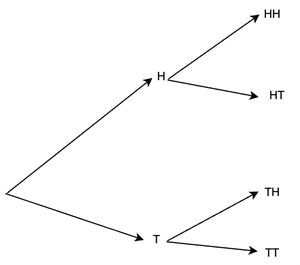
To illustrate this concept, let’s take this experiment as an example. 

A coin is tossed two times and the outcomes are recorded. The possible outcomes are: 

HH, HT, TH, TT

The figure below represents the outcomes in form of a tree. 

Notice that there are four possible outcomes in this experiment and none of them can be predicted beforehand. The set of all possible outcomes makes up the sample space for the random experiment. Thus, in the context of our experiment, the sample space is a universal set. It is denoted as S. For the above experiment, 

S = {HT, HH, TH, TT} 

When an experiment is repeated several times, each one of them is called a trial. Thus, a trial can be described as a particular performance of a random experiment. In this particular experiment, a trial is the tossing of the coin. Two such trials constitute the whole experiment. 

Events and Probabilities

For an experiment with sample space S, the goal is to assign probabilities to certain outcomes. To understand the concept of events, let’s consider an experiment again. Two dice are rolled, we are interested in the outcomes where the sum of the numbers of dice is equal to 6. The first step is to consider the sample space for this experiment. 

S = {(1,1); (1,2); …..(1, 6);

(2,1); (2,2); … (2,6);

(3,1); (3,2); ….(3,6);

(4,1); (4,2); …..(4,6);

(5,1); (5,2); ……(5,6);

(6,1); (6,2); ……(6,6);}

These are all the possible outcomes of this experiment. 

An event is the subset of the sample space. 

In this case, the event will be the outcomes where the sum of the number on the dice is equal to 6. It will contain all those outcomes from the set S, where the sum of the numbers is 6. Let’s say the event is denoted by E, 

E = {(2,4); (4,2); (3,3); (3,3); (1,5); (5,1)}

The cardinality of this set |E| = 6 while the cardinality of sample space |S| = 36.

Probability is defined as the ratio of the favorable number of outcomes and total number of possible outcomes

P(Event) = [Tex]\frac{\text{Favourable Number of Outcomes}}{\text{Total Number of Outcomes}}[/Tex]

For this case, 

P(E) = [Tex]\frac{\text{Favourable Number of Outcomes}}{\text{Total Number of Outcomes}}[/Tex]

⇒ P(E) = [Tex]\frac{|E|}{|S|}[/Tex]

⇒ P(E) = [Tex]\frac{6}{36}[/Tex]

⇒ P(E) = [Tex]\frac{1}{6}[/Tex]

Let’s look at some examples on these concepts.

Articles related to Probability:

• Probability in Maths
• Events in Probability
• Dependent and Independent Event
• Conditional Probability and Independence

Sample Problems on Random Experiment

Problem 1: Write the sample space for three tosses of a coin. 

Solution: 

A coin toss gives either Head (H) or Tails(T). 

Outcome of three coin tosses will be triplets of Heads and Tails. 

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} 

Problem 2: Out of the following activities given below. Choose random activities: 

1. Drawing a ball from an urn containing black and white balls.
2. Multiplying 4 and 8 on the calculator. 
3. Birth of a person

Solution: 

Each random experiment/activity must fulfill the following two conditions: 

1. The experiment can be repeated a number of times under the same conditions.
2. The outcome of the experiment cannot be predicted beforehand with certainty.

Drawing a ball from an urn containing black and white balls.

This can be repeated as many times as required, and also it cannot be predicted which ball will be drawn. Thus is a random activity. 

Multiplying 4 and 8 on the calculator. 

This activity can be repeated a number of times, but the result of this activity can be predicted beforehand. Thus, it is not a random activity. 

Birth of a person

Birth of a person cannot be repeated. So, it is not a random activity. 

Problem 3: Consider an experiment of rolling a die and then tossing a coin. Draw the sample space. 

Solution: 

A die when rolled given {1, 2, 3, 4, 5, 6} as result while a coin toss gives {H, T}. 

Sample space S = {(1, H); (2, H); (3, H); (4,H); (5,H); (6,H); (1, T); (2, T); (3, T); (4, T); (5, T); (6, T)}

Problem 4: Find the probability of getting 2 heads in three tosses of a coin. 

Solution: 

A coin toss gives either Head (H) or Tails(T). 

Outcome of three coin tosses will be triplets of Heads and Tails. So, the sample space is,

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} 

Counting the number of favorable outcomes, there are three outcomes with two heads. 

Probability = [Tex]\frac{\text{Favourable Number of Outcomes}}{\text{Total Number of Outcomes}}[/Tex]

P = [Tex]\frac{3}{8}[/Tex]

Problem 5: Find the probability of drawing out an ace from a well-shuffled deck of cards. 

Solution: 

A deck of cards contains 52 cards and out of which 4 are aces. The formula for probability, 

Probability = [Tex]\frac{\text{Favourable Number of Outcomes}}{\text{Total Number of Outcomes}}[/Tex]

Favorable Number of Outcomes = 4 

Total Number of Outcomes = 52 

Probability = [Tex]\frac{\text{Favourable Number of Outcomes}}{\text{Total Number of Outcomes}}[/Tex]

⇒ P = [Tex]\frac{4}{52}[/Tex]

⇒ P = [Tex]\frac{1}{13}[/Tex]

Problem 6: Find the probability of getting at least 1 head in three tosses of a coin. 

Solution: 

A coin toss gives either Head (H) or Tails(T). 

Outcome of three coin tosses will be triplets of Heads and Tails. So, the sample space is,

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} 

Counting the number of favorable outcomes, there are seven outcomes with atleast one head. 

Probability = [Tex]\frac{\text{Favourable Number of Outcomes}}{\text{Total Number of Outcomes}}[/Tex]

P = [Tex]\frac{7}{8}[/Tex]

Problem 7 : A fair coin is tossed three times. What is the probability of getting exactly two heads?

Solution:

Step 1: Identify the sample space.

The sample space consists of 8 possible outcomes: HHH, HHT, HTH, THH, HTT, THT, TTH, TTT

Step 2: Count favorable outcomes.

There are 3 outcomes with exactly two heads: HHT, HTH, THH

Step 3: Calculate the probability.

Probability = Number of favorable outcomes / Total number of outcomes

= 3 / 8

= 0.375 or 37.5%

Problem 8 : A standard deck of 52 cards has 4 aces. If you draw two cards without replacement, what is the probability of drawing two aces?

Solution:

Step 1: Calculate the probability of drawing the first ace.

P(first ace) = 4/52 = 1/13

Step 2: Calculate the probability of drawing the second ace, given that the first card was an ace.

P(second ace | first ace) = 3/51

Step 3: Use the multiplication rule of probability for independent events.

P(two aces) = P(first ace) × P(second ace | first ace)

= (1/13) × (3/51)

= 1/221

≈ 0.0045 or 0.45%

Problem 9: Two fair six-sided dice are rolled. What is the probability that the sum of the numbers is 7?

Solution:

Step 1: List all possible combinations that sum to 7.

(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)

Step 2: Count the number of favorable outcomes.

There are 6 combinations that sum to 7.

Step 3: Calculate the total number of possible outcomes.

Total outcomes = 6 × 6 = 36 (each die has 6 possible outcomes)

Step 4: Calculate the probability.

Probability = Number of favorable outcomes / Total number of outcomes

= 6 / 36

= 1 / 6

≈ 0.1667 or 16.67%

Problem 10 : A bag contains 3 red balls, 4 blue balls, and 5 green balls. If two balls are drawn without replacement, what is the probability that both balls are the same color?

Solution:

Step 1: Calculate the probability for each color separately.

For red: P(RR) = (3/12) × (2/11) = 1/22

For blue: P(BB) = (4/12) × (3/11) = 1/11

For green: P(GG) = (5/12) × (4/11) = 5/33

Step 2: Sum the probabilities for each color.

P(same color) = P(RR) + P(BB) + P(GG)

= 1/22 + 1/11 + 5/33

= 3/66 + 6/66 + 10/66

= 19/66

≈ 0.2879 or 28.79%

Practice Problems on Random Experiment

Problem 1: In a standard deck of 52 cards, what is the probability of drawing a heart?

Problem 2: A die is rolled. What is the probability of getting an even number?

Problem 3: A bag contains 4 red, 5 blue, and 3 green balls. What is the probability of drawing a blue ball?

Problem 4: Two coins are flipped. What is the probability of getting at least one head?

Problem 5: A box contains 3 defective and 7 non-defective items. If one item is selected at random, what is the probability that it is defective?

Problem 6: A single card is drawn from a standard deck of 52 cards. What is the probability of drawing a card that is either a king or a queen?

Problem 7: What is the probability of rolling a sum of 7 with two dice?

Problem 8: In a class of 30 students, 18 are female and 12 are male. What is the probability of randomly selecting a female student?

Problem 9: A bag contains 5 red, 7 yellow, and 8 black marbles. What is the probability of drawing a marble that is not red?

Problem 10: A student is selected at random from a group of 15 students, where 5 are freshmen, 7 are sophomores, and 3 are juniors. What is the probability that the student is a sophomore?

Problem 11: In a lottery, 4 numbers are drawn from a pool of 50 numbers. What is the probability of drawing the exact 4 winning numbers?

Problem 12: If you roll two dice, what is the probability of getting a sum greater than 9?

Problem 13: A box contains 8 white and 4 black balls. If 2 balls are drawn at random, what is the probability that both are white?

Problem 14: A restaurant offers 5 appetizers, 8 main courses, and 3 desserts. What is the probability of randomly choosing an appetizer and a dessert?

Problem 15: In a deck of 52 cards, what is the probability of drawing a card that is a spade or a 10?

Conclusion

In summary, random experiments and probability provide a framework for understanding and quantifying uncertainty. By analyzing sample spaces, events, and their probabilities, one can make informed predictions and decisions based on the likelihood of different outcomes. This foundational knowledge is crucial in various applications, from everyday decisions to complex scientific and business analyses.

FAQs on Random Experiment

What is a random experiment?

A random experiment is a process or event whose outcome cannot be predicted with certainty beforehand. It involves uncertainty and multiple possible outcomes.

What is probability in the context of a random experiment?

Probability measures the likelihood of occurrence of an event within a random experiment. It quantifies the chance of an outcome happening relative to all possible outcomes.

How is probability calculated?

Probability is calculated by dividing the number of favorable outcomes by the total number of possible outcomes. It typically ranges from 0 (impossible event) to 1 (certain event).

What are sample spaces and events in probability?

A sample space is the set of all possible outcomes of a random experiment. An event is any subset of the sample space, representing a particular outcome or combination of outcomes.

What are the basic rules of probability?

The basic rules of probability include the addition rule (for mutually exclusive events), the multiplication rule (for independent events), and the complement rule (for finding the probability of an event not occurring). These rules help calculate probabilities in various scenarios.