|
An ordered tree is an oriented tree in which the children of a node are somehow ordered. It is a rooted tree in which an ordering is specified for the children of each vertex. This is called a “plane tree” because the ordering of the children is equivalent to an embedding of the tree in the plane, with the root at the top and the children of each vertex lower than that vertex.
The ordered trees can be further specified as labelled ordered trees and unlabelled ordered trees.
Prerequisite: Catalan Numbers | Binomial Coefficient.
Labelled ordered trees: A labeled tree is a tree where each vertex is assigned a unique number from 1 to n.

If T1 and T2 are ordered trees. Then, T1 != T2 else T1 = T2.
Unlabelled ordered trees: An unlabelled tree is a tree where every vertex is unlabelled. Given below are the possible unlabelled ordered tree having 3 vertices.

The total number of unlabelled ordered trees having n nodes is equal to the (n – 1)-th Catalan Number.
Given below are the possible unlabelled ordered trees having 4 nodes. This diagram will work as a reference example for the next few results.
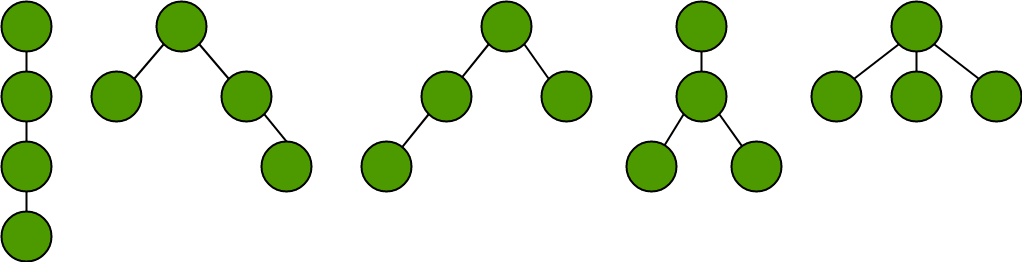
1. Number of trees with exactly k leaves.
Let us consider that we have ‘n’ edges. Then, the solution for the total possible ordered trees having ‘k’ leaves is given by :

2. Total number of nodes of degree d in these trees.
Let us consider that we have ‘n’ edges. Then, the solution for the total number of nodes having a degree ‘d’ is given by :

3. Number of trees in which the root has degree r.
Let us consider that we have ‘n’ edges. Then, the solution for the total possible ordered trees whose root has degree ‘r’ is given by :

Below is the implementation of the above combinatorics functions using Binomial Coefficient :
C++
<?php
function binomialCoeff($n, $k)
{
$C = array(array());
$i; $j;
for ($i = 0; $i <= $n; $i++) {
for ($j = 0; $j <= min($i, $k); $j++)
{
if ($j == 0 or $j == $i)
$C[$i][$j] = 1;
else
$C[$i][$j] = $C[$i - 1][$j - 1]
+ $C[$i - 1][$j];
}
}
return $C[$n][$k];
}
function k_Leaves( $n, $k)
{
$ans = (binomialCoeff($n, $k) *
binomialCoeff($n, $k - 1)) / $n;
echo "Number of trees having 4 edges and ",
"exactly 2 leaves : " , $ans ,"\n";
return 0;
}
function numberOfNodes( $n, $d)
{
$ans = binomialCoeff(2 * $n - 1 - $d, $n - 1);
echo "Number of nodes of degree 1 in"
, " a tree having 4 edges : " , $ans,"\n" ;
return 0;
}
function rootDegreeR( $n, $r)
{
$ans = $r * binomialCoeff(2 * $n - 1 - $r,
$n - 1);
$ans = $ans / $n;
echo "Number of trees having 4 edges"
, " where root has degree 2 : " , $ans ;
return 0;
}
k_Leaves(3, 2);
numberOfNodes(3, 1);
rootDegreeR(3, 2);
?>
|
Javascript
<script>
function binomialCoeff(n, k)
{
let C = new Array(n+1);
let i, j;
for (i = 0; i <= n; i++)
{
C[i] = new Array(k + 1);
for (j = 0; j <= k; j++)
{
C[i][j] = 0;
}
}
for (i = 0; i <= n; i++) {
for (j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1]
+ C[i - 1][j];
}
}
return C[n][k];
}
function k_Leaves(n, k)
{
let ans = parseInt((binomialCoeff(n, k) * binomialCoeff(n, k - 1)) / n, 10);
document.write( "Number of trees "
+ "having 4 edges and exactly 2 "
+ "leaves : " + ans + "</br>");
return 0;
}
function numberOfNodes(n, d)
{
let ans = binomialCoeff(2 * n - 1 - d,
n - 1);
document.write("Number of nodes "
+"of degree 1 in a tree having 4 "
+ "edges : " + ans + "</br>");
return 0;
}
function rootDegreeR(n, r)
{
let ans = r * binomialCoeff(2 * n - 1 - r, n - 1);
ans = parseInt(ans / n, 10);
document.write("Number of trees "
+ "having 4 edges where root has"
+ " degree 2 : " + ans + "</br>");
return 0;
}
k_Leaves(3, 2);
numberOfNodes(3, 1);
rootDegreeR(3, 2);
</script>
|
Output:
Number of trees having 4 edges and exactly 2 leaves : 3
Number of nodes of degree 1 in a tree having 4 edges : 6
Number of trees having 4 edges where root has degree 2 : 2
Time Complexity : O(n*k).
Auxiliary Space : O(n*k).*
|





