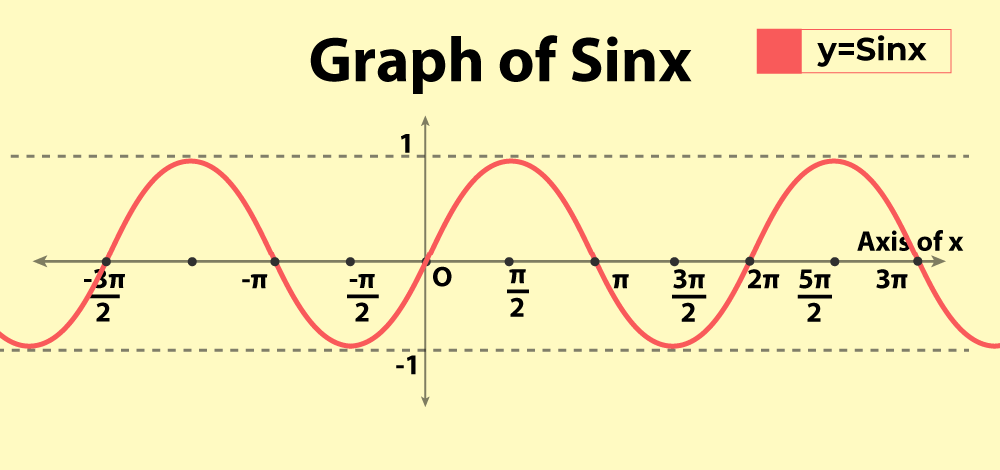
Sine and cosine functions are also some of the most basic functions that belong to the branch of mathematics called trigonometry and they are characterized by periodic oscillations; they are used in fields like physics, engineering and signal processing. These are used to describe waveforms and circular movements and are vital in such areas as sound waves light waves, and AC currents.

The purpose of this article is to include a discussion of the properties of sine and cosine functions and detailed guidance on how best to graph such functions, including a discussion of pitfalls that one ought to avoid.

What is a Sine Function?

The sine function is usually written as sin(x) and its graph is sinusoidal or oscillates in a smooth wave-like manner. In mathematics, the sine function refers to the y-coordinate of an object moving in the circumference of a circle that creates the unit circle area. The function goes through the range [-1,1] and has a period of 2π from the x-axis. The sine function is very important in the study of cyclical behaviours and is one of the main functions in trigonometry.

What is a Cosine Function?

The cosine function is noted as cos (x) and resembles the sine function with the only difference being that at x= 0 the function’s value is 1. It denotes the position of a figure in the x-coordinate axis of a circle whose circumference is one unit. This function has a range-like sine function that is [-1, 1] and its period is 2π. The cosine function is highly relevant to the oscillatory patterns and is in many cases partnered with the sine function.

Properties of Sine and Cosine Functions

Some of the properties of sine and cosine functions are as follows:

• Periodicity: Both functions repeat every 2π radians. This means sin(x+2π) = sin(x) and cos(x+2π) = cos(x).

• Amplitude: The amplitude is the maximum absolute value of the function, which is 1 for both sine and cosine functions. It indicates the height of the wave.

• Frequency: The frequency is the number of cycles the function completes in a unit interval. It is related to the period by f= 1/T, where T is the period.

• Phase Shift: This is the horizontal shift of the function. For y = sin(x-ϕ) or y = cos(x-ϕ), ϕ is the phase shift, which moves the graph left or right.

How to Graph Sine and Cosine Functions?

Graphing sine and cosine functions involves several steps to accurately represent their oscillatory behaviour.

Identifying Key Components

• Amplitude: Determines the peak and trough of the wave. For y = Asin(x) or y = Acos(x), the amplitude is ∣A∣.

• Period: Distance over which the function repeats. For y = sin(Bx) or y = cos(Bx), the period is 2π/B.

• Phase Shift: Horizontal displacement. For y = sin(Bx-C) or y = cos(Bx-C), the phase shift is C/B.

• Vertical Shift: Upward or downward displacement. For y = sin(x)+D or y = cos(x)+D, D is the vertical shift.

Graphing Sine Functions

To graph y = sin(x)

Identify the amplitude, period, phase shift, and vertical shift.

Plot the key points: Start from the origin, and identify maximum, minimum, and intercept points based on the period.

Draw the curve: Smoothly connect the points to form a wave.

For example, for y = 2sin (x-π/2) + 1

• Amplitude = 2
• Period = 2π
• Phase Shift = π/2 to the right
• Vertical Shift = 1

Graphing Cosine Functions

To graph y = cos(x)

Identify the amplitude, period, phase shift, and vertical shift.

Plot the key points: Start from the maximum value, identify the minimum, and intercept points based on the period.

Draw the curve: Smoothly connect the points to form a wave.

For example, for y = 3cos (2x+π) – 2

• Amplitude = 3
• Period = π
• Phase Shift = – π/2 to the left
• Vertical Shift = -2

Graphing Techniques and Tips

Various techniques for graphing sine and cosine functions are:

Using a Graphing Calculator

• Input sine and cosine functions: Enter the function into the calculator’s graphing mode.

Tips for accurately plotting the graphs:

• Adjust the window settings to capture the entire period.
• Use the zoom feature to refine the view of the graph.

Manual Graphing

• Creating a table of values: Select key points within one period and calculate their corresponding y-values.
• Plotting points and drawing the curve: Plot the calculated points on graph paper and smoothly connect them to form the sine or cosine wave

Common Mistakes to Avoid

Some mistakes to avoid while graphing sine and cosine function are:

• Ignoring Amplitude: Failing to account for amplitude can result in incorrect peak and trough values. The amplitude A determines the height of the wave, and neglecting it will lead to inaccurate graph scaling.

• Incorrect period calculation: The period P of the function is essential for plotting. Miscalculating the period (for y = sin(Bx) or y = bcos(Bx), the period is 2π/∣B∣) will distort the wave’s frequency.

• Ignoring phase shift: Phase shift C/B moves the graph horizontally. Forgetting this shift can place key points incorrectly along the x-axis.

• Neglecting vertical shift: Vertical shift D moves the graph up or down. Overlooking this will misplace the midline of the wave.

• Inaccurate plotting: Failing to plot enough points within one period can lead to a jagged and inaccurate curve. Ensure a smooth wave by plotting sufficient points.

Conclusion

Sine and cosine functions are the key ideas of calculus, which are used to describe oscillation in many scientific disciplines. Students are not a stranger with functions like these and with an understanding of their properties as well as techniques in graphing them, they can represent them in the best way possible. It presents a systematic methodology for graphing, the most important aspects to bear in mind, and the most frequent mistakes to be avoided to get a concise and orderly plot of sine and cosine functions.

FAQs on Graphing of Sine and Cosine Functions

What features are unique to sine and cosine graphs?

Sine and cosine graphs are both periodic with a period of 2π, and have amplitude values of 1 and bounded between -1 and 1.

In what ways can the graphs of sine and cosine be transformed?

The graphs can be shifted vertically and horizontally, stretched or compressed, and reflected across the x-axis or y-axis.

Are sine and cosine graphs continuous?

Yes, sine and cosine graphs are continuous for all real numbers.

What are the origins of sine and cosine graphs?

Both graphs originate from the unit circle, representing the y-coordinates (sine) and x-coordinates (cosine) of points on the circle.

Are sine and cosine odd functions?

The sine function is odd (sin(-x)=-sin(x)), while the cosine function is even (cos(-x)=cos(x)).