Absolute Value Function or Modulus Function, commonly denoted as f(x)=∣x∣, is a fundamental concept in mathematics. It represents the distance of a number from zero on the number line, regardless of direction. This means that the absolute value of both -5 and 5 is 5 because both numbers are five units away from zero.

This function is widely used in various fields to measure distances and analyze real-world problems. For instance, it is used in engineering to specify tolerance ranges and in statistics to measure deviations from a central value.

In this article, we will discuss the absolute value function in detail including its definition, properties as well as graph.

What is Absolute Value Function?

An absolute value function, denoted as ∣x∣, is a mathematical function that returns the non-negative value of a number without regard to its sign. In simple words, we can say the absolute value of a number is its distance from zero on the number line, no matter which direction (positive or negative) it is. Mathematically, the absolute value function is defined as:

[Tex]y=|x|=\begin{cases} x,& x \ge 0 \\ -x, & x<0 \end{cases}[/Tex]

Examples: |3| = 3, |-1| = 1, and |0| = 0

Properties of Absolute Value Function

Some of the common properties related to the Absolute Value Function are:

• Idempotent
• Non-negativity
• Multiplicity
• Positive Definiteness
• Symmetry
• Triangular Inequality
• Properties of Absolute Value Inequalities

Idempotent

A function f(x) is idempotent if and only if f(f(x)) = f(x). The modulus function f(x) = |x| is idempotent because applying the modulus function twice does not change the result:

[Tex]|\,|x|\,| = |x| \,;\,x\in\R[/Tex]

Non-negativity

The absolute value of any real number is always non-negative.

[Tex]|x| \ge 0;[/Tex] for all [Tex]x\in\R[/Tex]

Multiplicity

The absolute value of the product of two numbers is equal to the product of the individual moduli of both numbers.

[Tex]|ab|=|a||b|[/Tex] for all [Tex]a,\,b\in\R[/Tex]

Positive Definiteness

The absolute value of x is zero if and only if x is zero.

[Tex]|x|=0\iff x=0[/Tex]

Symmetry

The absolute value function |x| is symmetric with respect to origin. Mathematically, this is repesented by:

[Tex]|-x|=|x|[/Tex]

Triangular Inequality

The modulus of the sum of two numbers is less than or equal to the sum of the moduli of the individual numbers. If a, b [Tex]\in\R[/Tex], then:

[Tex]|a+b|\le|a|+|b|[/Tex]

The triangle inequality has several variations. Here are three common forms:

• If a,b [Tex]\in\R[/Tex], then [Tex]|\,|a|-|b|\,|\le|a-b|[/Tex].
• If a,b [Tex]\in\R[/Tex], then [Tex]|a-b|\le|a+b|[/Tex].
• If [Tex]a_1,a_2,a_3,… ,a_n[/Tex] are any real numbers, then [Tex]|a_1+a_2+a_3+…+a_n|\le|a_1|+|a_2|+|a_3|+…+|a_n|[/Tex].

Properties of Absolute Value Inequalities

Some of the common properties of the modulus function involving inequalities are:

• If c[Tex]\ge[/Tex], then |a|[Tex]\le[/Tex]c if and only if [Tex]-c\le a\le c[/Tex].
• If b is a real number, then [Tex]-|b|\le b\le|b|[/Tex].
• If a and b are real numbers, then [Tex]|a|\ge b[/Tex] if and only if [Tex]a\in (-\infty,-b]\cup[b,\infty)[/Tex].

Graph of Absolute Value Function

In general, the graph of a modulus function is V-shaped. For example, the graph of the modulus function |x| is V-shaped with its vertex at the origin. To plot the graph of a modulus function, we need to simplify the modulus expression based on the sign of the function inside the modulus. This involves finding the intervals in which the function is positive or negative.

After simplifying, plot the graph of each individual equation obtained by simplifying the modulus function. For example, let us plot the graph of y=|x|. By the definition of modulus function, |x| can be simplified in following manner,

[Tex]y=|x|=\begin{cases} x,& x \ge 0 \\ -x, & x<0 \end{cases}[/Tex]

1. For x[Tex]\ge0[/Tex], the equation is y = x, which is straight line passing through origin with slope of 1.

2. For x < 0, the resultant equation is y = -x, which is a straight line passing through origin with slope -1. After plotting the graph of both equation, we obtain the plot of y = |x|, as shown below:

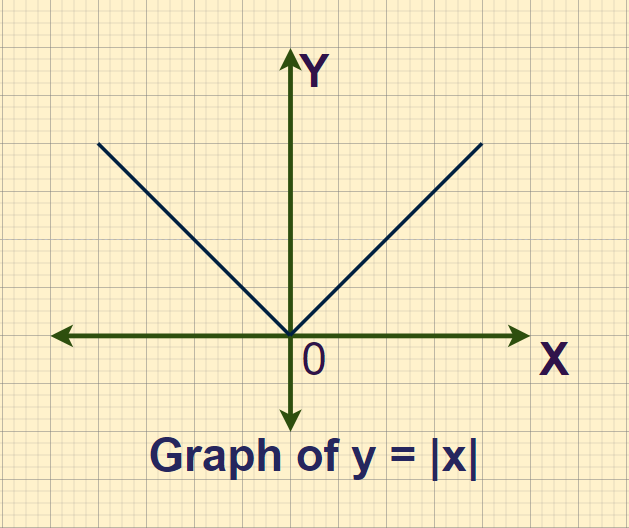By observing the above graph, we can see that the graph of |x| is symmetric about y-axis. This is known as the symmetric property of modulus function. The line of symmetry passes through vertex of absolute value function. The vertex is the point where the graph changes direction.

Absolute Value Function of Complex Number

The absolute value of any complex number gives the distance of that number from the origin. If z is a complex number, z=[Tex]x+\iota y[/Tex] then the absolute value of z, denoted as |z|, gives the distance of z from the origin and is given below:

[Tex]|z| = |\ x \ + \ y\iota| = \sqrt{x^2 \ + \ y^2}[/Tex]

Example: Find the distance of z=[Tex]4+3\iota[/Tex] from the origin.

Solution:

Absolute value of z is,

[Tex]|z| = |4+3\iota| \\ |z| = (\ 4^2 \ + \ (3)^2)^1 \ ^/ \ ^2 \\ |z| = (\ 16 \ + \ 9)^1 \ ^/ \ ^2\\ |z| = (25)^1 \ ^/ \ ^2\\ |z| = 5[/Tex]

Thus, the distance of z from origin is 5 unit, the graphical representation of z=[Tex]4+3i[/Tex] is given by following plot.

Absolute Value Function in Calculus

In calculus we study continuity, differentiablity, derivative and integration of absolute value function.

Continuity of Absolute Value Function

A function f(x) is continuous at point x=a if the function satisfies the following condition:

[Tex]\lim_{x \to a} f(x)= f(a) \\ \lim_{x \to a^-} f(x)= f(a^-) = f(a) \quad \text{[Left hand limit]} \\ \lim_{x \to a^+} f(x)= f(a^+) = f(a) \quad \text{[Right hand limit]} [/Tex]

Example: Check the continuity of y = |x| at x = 0.

Solution:

[Tex]\lim_{{x \to 0^+}} |x| = \lim_{{x \to 0^+}} x = 0 \quad \text{[Right Hand Limit]} \\ \lim_{{x \to 0^-}} |x| = \lim_{{x \to 0^-}} (-x) = 0 \quad \text{[Left Hand Limit]} \\ \therefore f(0^-) = f(0^+) = f(0) = 0 [/Tex]

Since the limit exists at [Tex]x = 0[/Tex] and it is equal to value of [Tex]y=|x|[/Tex] which is 0 ,the function [Tex]y = |x|[/Tex] is continous at [Tex]x = 0[/Tex].

Differentiability of Absolute Value Function

A function f(x) is differentiable at a point x=c if the derivative exists at that point and it is given by,

[Tex]f'(c)\ =\ \lim_{{h \to 0}}\frac{f(c+h) – f(c)}{h} [/Tex]

Example: Check differentiability of [Tex]y=|x|[/Tex] at [Tex]x=0[/Tex].

Solution:

[Tex]f'(0) \ =\ \lim_{{h \to 0}} \frac{|0+h| – |0|}{h} = \lim_{{h \to 0}} \frac{|h|}{h}[/Tex]

For h > 0:
[Tex]\lim_{{h \to 0^+}} \frac{|h|}{h} = \lim_{{h \to 0^+}} \frac{h}{h} = 1[/Tex].

For h < 0:
[Tex]\lim_{{h \to 0^-}} \frac{|h|}{h} = \lim_{{h \to 0^-}} \frac{-h}{h} = -1[/Tex].

Since, the value of left hand limit and right hand limit are not equal, the limit doesn’t exist. And hence, the function [Tex]y=|x|[/Tex] is not differentiable at x=0.

Derivative of Absolute Value Function

The derivation of moudulus function f(x) is given by,

[Tex]\frac{d}{dx}|f(x)|=\begin{cases} \frac{d}{dx}f(x)\quad &;f(x)>0\\ \frac{d}{dx}(-f(x))\quad &;f(x)<0 \end{cases}[/Tex]

Example: Find the derivative of y=|x| for all x[Tex]\in\R[/Tex].

Solution:

When x>0:
[Tex]\frac{d}{dx}|x|=\frac{d}{dx}x=1[/Tex]

When x<0:
[Tex]\frac{d}{dx}|x|=\frac{d}{dx}(-x)=-1[/Tex]

Integration of Absolute Value Function

Integration involving the absolute value function can be solved using its properties: if the expression inside the modulus is positive, the modulus can be removed with a positive sign; if the expression inside the modulus is negative, the modulus can be removed with a negative sign

To integrate such functions, it’s necessary to identify the points where the expression inside the modulus changes sign. We then split the integral at these points and integrate the resulting expressions accordingly. This method allows us to handle absolute value functions effectively in integration problems.

Example: Find the value of integral [Tex]I =\int\limits_{-5}^{5} |x| \, dx[/Tex].

Solution:

[Tex]|x|=\begin{cases} \ \ x \quad;&x \ge 0 \\ -x \quad;&x<0 \end{cases}[/Tex]

then,
[Tex]I=\int\limits_{-5}^{5} |x|\,dx \\I=\int\limits_{-5}^{0} |x|dx+\int\limits_{0}^{5} |x|dx\\ \\ I=\int\limits_{-5}^{0} (-x)dx+\int\limits_{0}^{5} x \ dx \\I =-\int\limits_{-5}^{0} (x)dx+\int\limits_{0}^{5} x \ dx \\I=-[\frac{x^2}{2}]_{-5}^{0}+ [\frac{x^2}{2}]_{0}^{5}\\I=-[\frac{0^2}{2}-\frac{(-5)^2}{2}]+[\frac{5^2}{2}-\frac{0^2}{2}] \\I=0+ \frac{25}{2} + \frac{25}{2}-0 \\ \therefore I=25 [/Tex]

Conclusion-Absolute Value Function

In this article on the absolute value function, we have discussed what absolute value functions are, their properties, and how to plot their graphs. Additionally, we have seen some solved examples and performed differentiation and integration involving the absolute value function. We have also checked the continuity and differentiability of the absolute value function.

Examples on Absolute Value Function

Example 1: Find the value of x for |x-2| = 3.

Solution:

First, Identify the value of x for which the expression inside the modulus function becomes zero.

In this example, the function inside the modulus, f(x) = x-2, becomes zero at x=2.

By definition of absolute value function, when x>2 the modulus will open with positive sign and when x<2 it will open with negative sign.

For [Tex]x\ge2[/Tex]:

|x-2| = 3

x-2 = 3

x = 5

And for x < 2:

|x-2| = 3

-(x-2) = 3

x – 2 = -3

x = -3+2

x = -1

Therefore, the value of x are 5 or -1.

Example 2: Find the value of x for |x-5| = 0.

Solution:

In this question when x is greater than 5 it will open will positive sign and it will open with negative sign when x is less than 5.

For [Tex]x\ge0[/Tex] and [Tex]x<0[/Tex],

|x-5| = 0

±(x-5) = 0

x-5 = 0

x = 5

Example 3: Solve the inequality for x: |x-4| > 3.

Solution:

Inequality |x-4| > 3 means that the distance between x and 4 is greater than 3.

This can be split into two separate inequalities:

1. When x>4, the inequality becomes x-4>3.
2. When x<4, the inequality becomes -(x-4)>3, which is equivalently x-4 < -3.

Now, let’s solve these inequalities separately.

Solving the inequality when x>4:
[Tex]\Rightarrow[/Tex]x-4>3

Adding 4 to both sides, we get:
[Tex]\Rightarrow[/Tex]x>7

Solving the inequality when x<4:
[Tex]\Rightarrow[/Tex]x-4<-3

Adding 4 to both sides, we get:
[Tex]\Rightarrow[/Tex]x<1

The solution to |x-4|>3 is the union of the solutions to the two cases:
[Tex]\Rightarrow x>7 \,\cup\,x<1\\\Rightarrow x\in(-\infty,1)\cup(7,\infty)[/Tex]

Example 4: Solve the inequality for x: [Tex]\frac{|x-4|}{|x+4|}>0[/Tex].

Solution:

[Tex]\Rightarrow\frac{|x-4|}{|x+4|}>0[/Tex]

The above inequality can be rearranged to:
[Tex]\Rightarrow\frac{|x-4|}{|x+4|}\cdot|x+4|>0\cdot |x+4|[/Tex]

Since |x+4| is a positive quantity, it does not affect the inequality. Therefore, for [Tex]x\in\R-\{-4\}[/Tex]:
[Tex]\Rightarrow[/Tex]|x-4|>0

Using the property, [Tex]|a|\ge b\iff a\in (-\infty,-b]\cup[b,\infty)[/Tex] we get:
x-4 > 0 or x-4 < 0

Adding 4 on both sides:

x > 4 or x < 4

Therefore, the final solution will be:
[Tex]\Rightarrow x\in(-\infty,4)\cup(4,\infty)-\{-4\}[/Tex] or [Tex]x\in\R\,-\,\{-4,4\}[/Tex].

Example 5: Solve the inequality for x: |x-4|(x-5) > 0.

Solution:

Critical points are x = 4, and x = 5, where the product is zero. The expression |x-4| is always non-negative, and the factor x-5 is greater than zero when x>5.

Therefore, the expression |x-4|(x-5) is greater than zero if and only if x > 5.

Solution will be: x > 5

Practice Questions on Absolute Value Function

Q1. Find the value of x in the following equations.

1. |x-1| = 1
2. |3x+5| = 0
3. |x|(x+2) = 5
4. [Tex]\frac{x}{|x-1|}[/Tex] = 3
5. |2x-4| = |x+2|

Q2. Solve the following inequalities.

1. |x-3| < 1
2. |3x+1| [Tex]\le[/Tex] 4
3. |2x-3| [Tex]\ge[/Tex] 3
4. [Tex]\frac{|x|}{|x+1|}[/Tex] < 2
5. [Tex]|1+\frac{4}{x}|[/Tex] > 5

Q3. Prove the following.

1. [Tex]|a^2|=|a|^2[/Tex]
2. [Tex]|a^3|=|a|^3[/Tex]

Q4. Find the point at which the function is not differentiable.

1. |x-1|
2. |2x+5|
3. [Tex]\frac{1}{3x-7}-5[/Tex]

Answer Key

Answer key for Q1

1. x = 2 or 0
2. x = [Tex]\frac{-5}{3}[/Tex]
3. x = [Tex]-1-\sqrt{6}[/Tex] or [Tex]-1+\sqrt{6}[/Tex]
4. x = [Tex]\frac{2}{3}[/Tex] or [Tex]\frac{3}{4}[/Tex]
5. x = 6 or [Tex]\frac{2}{3}[/Tex]

Answer key for Q2

1. 2 < x < 4
2. [Tex]-\frac{5}{3} \le x \le 1[/Tex]
3. [Tex]x\in(-\infty,0] \cup[3,\infty)[/Tex]
4. [Tex]-2<x<-1[/Tex] or [Tex]-\frac{2}{3}<x<2[/Tex]
5. [Tex]x<-\frac{2}{3}[/Tex] or [Tex]0<x<1[/Tex]

Answer key for Q4

1. x = 1
2. x = [Tex]\frac{-5}{2}[/Tex]
3. x = [Tex]\frac{7}{3}[/Tex]

Related Articles:

• Continuity of Functions
• Differentiability of a Function
• Derivative of a Function
• Integration
• Inequality
• Complex Numbers

FAQs on Absolute Value Function

How is the absolute value function used in solving equations and inequalities?

Absolue value function is used for solving question which is based on inequalities and also to solve equations by breaking them into two parts, one for when expression inside the absolute value is positive and other for when it is negative.

For example, solving [Tex]|x-3| = 5[/Tex] involves solving the two equation [Tex]x-3 = 5[/Tex] and [Tex]x-3 = -5[/Tex]

Is the absolute value function continuous and differentiable?

Absolute value function [Tex]y=|x|[/Tex] is continuous everywhere but not differentiable at [Tex]x=0[/Tex].

What are the graphical characteristics of the absolute value function?

Graph of the absolute value function is a V-shape with its vertex at the point where the value of the function becomes minimum or zero. For example, the vertex of [Tex]y=|x|[/Tex] is at [Tex]x=0[/Tex], When [Tex]x>0[/Tex], the graph is a straight line with a slope of 1, and for [Tex]x<0[/Tex], it is a straight line with a slope of -1.

This symmetry about the y-axis makes it an even function.

What are applications of the absolute value function in real life?

Some of real life application of absolute value function are as follows:

• Engineering: Measuring deviations from a desired value.
• Economics: Calculating differences in costs, prices, and profits.
• Physics: Determining magnitudes of vectors.
• Statistics: Calculating measures like the mean absolute deviation.

How do you solve equations involving the absolute value function?

To solve equations involving [Tex]∣x∣[/Tex], you often need to consider the different cases where the expression inside the absolute value is non-negative and negative.

For example, to solve [Tex]∣x∣=a[/Tex], you consider [Tex]x=a[/Tex] and [Tex]x=−a.[/Tex]