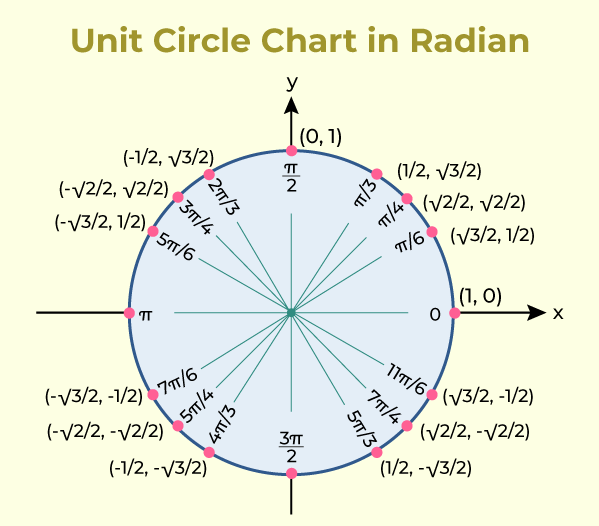
Trigonometry on the unit circle is a fundamental concept that ties together geometry and algebra with the study of angles and their associated trigonometric functions.

In this article, we will learn what Unit Circle Trigonometry is, also solve some problems, etc.

What is Unit Circle Trigonometry?

Unit Trigonometry refers to the study of trigonometric functions using the unit circle, a circle with a radius of one-centred at the origin of a coordinate plane. In this approach, angles are measured in radians and their sine, cosine, and tangent values are derived based on their coordinates on the unit circle. For instance, the cosine of an angle is the x-coordinate of the point where the terminal side of the angle intersects the unit circle, and the sine is the y-coordinate. Unit trigonometry simplifies calculations and provides a clear geometric interpretation of trigonometric functions.

Unit circle is a circle with a radius of 1, centred at the origin of a coordinate plane. It’s used to define trigonometric functions for all real numbers.

Formula For Unit Circle

Any point P on the unit circle can be described in terms of its coordinates (x,y). Since the radius of the unit circle is 1, the coordinates of any point on the circle satisfy the following equation:

x² + y² = 1

This equation is derived from the Pythagorean theorem, considering that the radius is the hypotenuse of a right-angled triangle with legs x and y.

• Unit Circle Definition: A circle with a radius of 1, centered at the origin (0,0).

• Equation of the Unit Circle: For any point P(x,y) on the unit circle,

x²+y²=1

Trigonometric Functions on Unit circle

Various trigonometric function on unit circle are:

Sine Function (sin⁡): Represents the y-coordinate of the point P on the unit circle. sin⁡(θ) = y

Cosine Function (cos⁡): Represents the x-coordinate of the point P on the unit circle. cos⁡(θ) = x

Tangent Function (tan⁡): Represents the ratio of sine to cosine on the unit circle. tan⁡(θ) = sin⁡(θ)/cos⁡(θ)

Unit Circle-Trigonometry: Practice Problems

P1. Solve for x in the equation 2sin⁡(x)-1=0.

Solution:

Rearrange the Equation:

2sin⁡(x) = 1  

⇒ sin⁡(x) = 1/2

Angles where sin⁡(x) = 1/2 are x = 30^∘ and x = 150^∘ in the range 0^∘ to 180^∘.

For other ranges, you would use:

x = 30^∘+ 360^∘k or x = 150^∘ + 360^∘k where k is an integer.

P2. Find tan⁡(60^∘).

Solution:

Using the 30-60-90 triangle, where the side ratios are 1:root3:2

tan⁡(60^∘) = opposite/adjacent

tan⁡(60^∘) = √3

P3. If sin⁡(A)=3/5​, find cos⁡(A)and tan⁡(A).

Solution:

Using the Pythagorean identity sin⁡²(A) + cos^⁡2(A) = 1

sin⁡²(A) = (3/5)² = 9/25

cos⁡²(A) = 1-9/25 = 16/25

cos(A) = ±4/5​

Sign of cos⁡(A) depends on the quadrant.

For tan⁡(A):

tan⁡(A) = sin⁡(A)/cos⁡(A)

= (3/5)/(4/5)

= 3/4

P4. Solve cos⁡²(x) – sin⁡²(x) = 1/2​.

Solution:

Use the identity cos⁡²(x) – sin⁡²(x) = cos⁡(2x)

cos⁡(2x) = 1/2

Angles where cos⁡(2x) = 1/2 are 2x = 60^∘and 2x = 300^∘.

Thus:

2x = 60^∘ + 360^∘k or 2x = 300^∘ + 360^∘k

x = 30^∘ + 180^∘k or x = 150^∘ + 180^∘k; where k is an integer.

P5. Find tan⁡(45^∘).

Solution:

tan⁡(45^∘) = 1 (using trigonometric table)

P6. If sin⁡(x)=4/5​, find cos⁡(x).

Solution:

cos^⁡2(x) = 1-sin⁡²(x)

= 1 – (4/5)²

= 1 – 16/25

= 9/25

cos⁡(x) = ±3/5

Practice Questions on Unit Circle-Trigonometry

Q1. If cos⁡(x) = 1/2, find x in the range 0^∘ to 360^∘.

Q2. Solve sin⁡(x) = 0.

Q3. Find cot⁡(30^∘).

Q4. Find the reference angle for 210^∘.

Q5. Find sin⁡(90^∘-θ).

Q6. Find cos⁡(2θ) using the double-angle formula.

Q7. Find sin⁡(120^∘).

Q8. Find sin^⁡2(x) + cos⁡²(x)

Applications of Unit Circle Trigonometry

Some applications of unit circle trigonometry are:

• Angles and Measurements: Allows for precise measurement and calculation of angles in geometry, physics, and engineering.
• Function Analysis: Understanding the periodic nature of trigonometric functions and their graphical representations.
• Vectors and Rotations: Useful in describing rotational motion and vector components in 2D and 3D space.

Conclusion

Unit circle trigonometry provides a foundational understanding of angles and their associated functions in both theoretical and practical contexts. It serves as a basis for more advanced topics in calculus, physics, and engineering, making it an essential concept in mathematics education. By visualizing angles as points on the unit circle and understanding their relationships through trigonometric functions, one gains insight into the fundamental properties of geometry and algebra.

Frequently Asked Questions

What is a Unit Circle?

Unit circle is a circle with a radius of 1, centred at the origin of a coordinate plane. It’s used to define trigonometric functions for all real numbers.

Why is Unit Circle important in Trigonometry?

Unit circle allows us to define the sine, cosine, and tangent functions for all angles, extending beyond right triangles to include any angle, including those greater than 90 degrees and negative angles.

How are Sine and Cosine defined using the Unit Circle?

For an angle θ measured from the positive x-axis, the coordinates of the point where the terminal side of the angle intersects the unit circle are (cosθ, sinθ).

How is Tangent Function defined using Unit Circle?

Tangent of an angle θ is defined as tan⁡θ = sin⁡θ/cos⁡θ​. It represents the slope of the line formed by the terminal side of the angle.

How can Unit Circle be Used to Solve Real-World Problems?

Unit circle can model periodic phenomena such as sound waves, light waves, and seasonal changes. It’s also used in engineering, physics, and computer graphics for rotations and oscillations.

What is Relationship between Unit Circle and Pythagorean Identity?

Pythagorean identity sin⁡²θ + cos⁡²θ = 1 directly follows from the definition of sine and cosine on the unit circle, where the radius is always 1.