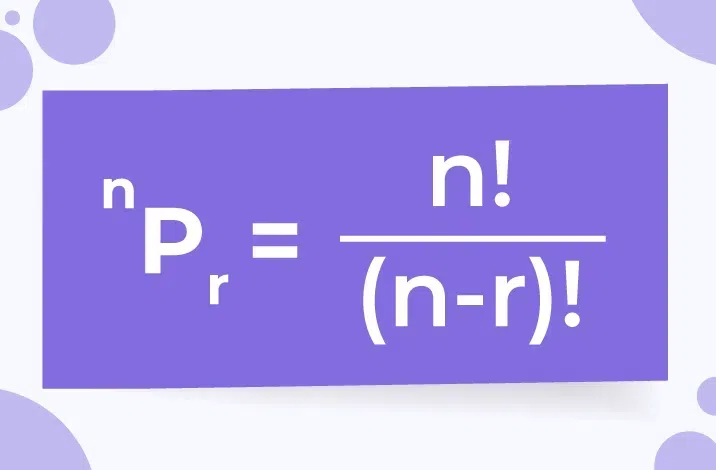
Answer: Yes, Order Matters in Permutations.

What is Permutation?

In mathematics, a permutation is an arrangement of a set of objects in a particular order. Each permutation is a unique sequence where the order of elements matters. For example, given a set {A, B, C}, the permutations ABC, ACB, BAC, BCA, CAB, and CBA are all distinct because they arrange the elements in different orders.

Definition

A permutation refers to an arrangement or ordering of a set of distinct elements. In simpler terms, a permutation is a specific way of arranging items in a sequence or set, where each arrangement is considered distinct if the order of elements is different.

Permutation Formula

The formula of permutation calculates the number of ways to arrange r items selected from a set of n items, where the order of the items matters. It is represented as:

[Tex]^{n}\textrm{P}_{r} = \frac{n!}{(n-r)!}[/Tex]

where,

• n is the total number of objects
• r is the number of objects chosen, 0 ≤ r ≤ n

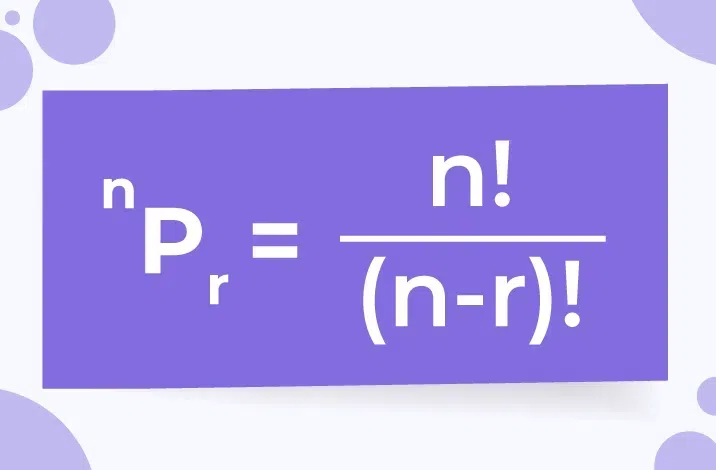Does Order Matter in Permutations

Yes, in permutations, the order does matter. Permutations are arrangements of elements where the order of selection is important. For example, if you have a set of elements {1, 2, 3}, the permutations include arrangements like 123, 132, 231, 213, 312 and 321. Each permutation is distinct because the order of the elements is different in each case.

The number of permutations of a set of n distinct objects is given by n factorial (n!), which grows exponentially as n increases. Taking all the possible arrangements where order matters, this factorial shows the total number of ways those things can be arranged.

However, in the case of combinations, the order does not matter. Combinations are used to select a subset of items randomly chosen from a bigger collection, regardless of the order in which they are selected. the same elements. For example, the combinations of {A, B, C} include ABC and BAC, CAB, etc., treating these selections as the same group because they contain the same elements.

Related Examples

Example 1: Find the number of permutations of 3 distinct letters taken 2 at a time.

Solution:

Given n = 3 (let distinct letters: A, B, C) and r=2.

Number of permutations P(3, 2) is calculated using the formula: P(n,r)= n!/(n−r)!

So, P(3, 2)= 3!/(3−2)!

= 3!/1! = 6

Permutations are:

AB, AC, BA, BC, CA, CB.

Therefore, there are 6 different permutations of 3 distinct letters taken 2 at a time.

Example 2: How many ways can 4 people (A, B, C, D) be arranged in a line?

Solution:

Here, n=4 (people: A, B, C, D).

Number of permutations P(4,4) is: 4!/(4−4)!

= 4!/0! = 24/1 = 24

Therefore, there are 24 different ways to arrange 4 people (A, B, C, D) in a line.

Example 3: In how many ways can the letters of the word “BOOK” be arranged?

Solution:

Word “BOOK” consists of 4 letters where ‘O’ appears twice.

Number of permutations is calculated by dividing the factorial of the total number of letters by the factorial of the repetitions:

4!/2! = 24/2

=12

So, there are 12 different ways to arrange the letters in the word “BOOK”.

Example 4: How many permutations can be made from the letters of the word “APPLE”?

Solution:

Word “APPLE” consists of 5 letters where ‘P’ appears twice.

Number of permutations P(5,5) considering repetitions:

5!/2! = 120/2

= 60

​Therefore, there are 60 different permutations of the letters in the word “APPLE”.

Example 5: In how many ways can 3 books (Book A, Book B, Book C) be arranged on a shelf?

Solution:

Here, n = 3 (books: A, B, C).

Number of permutations P(3,3) = 3!/0! = 6

Thus, there are 6 different ways to arrange 3 books (Book A, Book B, Book C) on a shelf.

Example 6: A team of 5 students (Alex, Bob, Carol, Dave, Eve) is to be arranged in a row for a photo. In how many ways can they be arranged?

Solution:

Here, n = 5 (students: Alex, Bob, Carol, Dave, Eve).

Number of permutations P(5, 5):

P(5, 5) = 5!/0! = 120

So, there are 120 different ways to arrange the 5 students in a row.

Example 7: How many different license plates can be made using 3 letters followed by 3 digits (assuming each letter or digit can be used more than once)?

Solution:

For the letters, n=26 (26 letters in the alphabet).

For the digits, n=10 (0-9 digits).

Number of permutations for the license plate format (LLLDDD):

P(26,3) × P(10,3)= 26!/(26−3)! × 10!/(10−3)!

= [26×25×24×23!/23!] × [10×9×8×7!/7!]

​=26×25×24×10×9×8

=1,872,000

Therefore, there are 1,872,000 different license plates possible with this format.

Example 8: How many different ways can 4 different awards (Gold, Silver, Bronze, and Iron) be distributed among 4 competitors (Alice, Bob, Carol, and Dave)?

Solution:

Each award must go to a different competitor, so we are looking for permutations of competitors receiving awards.

Number of permutations P(4,4):

P(4,4) = 4!/0! =24

Thus, there are 24 different ways to distribute the awards among the 4 competitors.

Practice Problems

Problem 1: How many permutations can be made from the letters of the word “BANANA”?

Problem 2: In how many ways can 4 books (Book X, Book Y, Book Z, Book W) be arranged on a shelf?

Problem 3: A group of 6 people (Alice, Bob, Carol, David, Eve, Frank) are to stand in a line for a photograph. In how many different ways can they arrange themselves?

Problem 4: How many different 4-digit numbers can be formed using the digits 1, 2, 3, and 4, without repetition of digits?

Problem 5: In a spelling competition, there are 8 contestants. In how many ways can the first, second, and third places be awarded prizes if ties are not allowed?

Problem 6: A team of 7 basketball players are to be arranged in a line for a team photo. In how many ways can they arrange themselves if the point guard and center refuse to stand next to each other?

Problem 7: How many different ways can the letters of the word “COMPUTER” be arranged?

Problem 8: A committee of 5 members is to be formed from 10 people. In how many ways can this be done if the order of selection does not matter?

Problem 9: How many different arrangements can be made of the digits 2, 3, 4, 5, 6, 7, 8 if no digit is repeated?

Problem 10: In how many ways can 5 different books (Book A, Book B, Book C, Book D, Book E) be arranged on a shelf if Book A must always be to the left of Book B?

Read More,

• Permutations and Combinations
• How many permutations can be formed by sampling 5 items out of 8?
• How many 4 digit numbers can be formed using the numbers 1, 2, 3, 4, 5 with digits repeated?

FAQs

What is the General Rule for Permutation?

If you have n distinct objects, the number of permutations of r objects taken at a time is given by:

P(n, r) = n! / (n-r)!

What are the Limitations of Permutations?

Limitations of permutations include:

• Complexity with Large Numbers: Calculating permutations becomes difficult as n and r increase.
• Permutations may not be feasible to calculate directly for very large sets due to factorial growth.

How is a Permutation Different from a Combination?

• Permutation: Order matters. For instance, AB is different from BA.
• Combination: Order doesn’t matter. AB is the same as BA.

A group of 5 friends wants to take a picture. In how many different ways can they arrange themselves in a row?

This is a permutation problem as the order of the friends matters.

n = 5 (total number of friends)

r = 5 (all friends are arranging themselves)

P(5, 5) = 5! / (5-5)! = 5! / 0! = 120 ways.

How can you determine if order matters in a problem?

You can easily determine if order matters in a problem by considering whether the sequence or arrangement of items is significant:

• If the problem asks for different sequences or arrangements where the order affects the outcome, then order matters, and you should use permutations.
• If the problem simply asks for groups or selections where the order does not affect the outcome, then order does not matter, and you should use combinations.