Detecting cycles in a graph is a fundamental problem in computer science and has various applications, including detecting deadlocks in operating systems, analyzing network structures, and more. This article explores how to detect cycles in both directed and undirected graphs using the C programming language.

What is a graph?

A graph G consists of vertices (or nodes) and edges connecting these vertices. Depending on the direction of the edges, graphs can be categorized into:

• Directed Graphs: The edges have a direction, going from one vertex to another.
• Undirected Graphs: The edges do not have a direction and simply connect two vertices.

Cycle Detection in Directed Graphs

A cycle in a directed graph is a path that starts and ends at the same vertex with all edges following the direction.

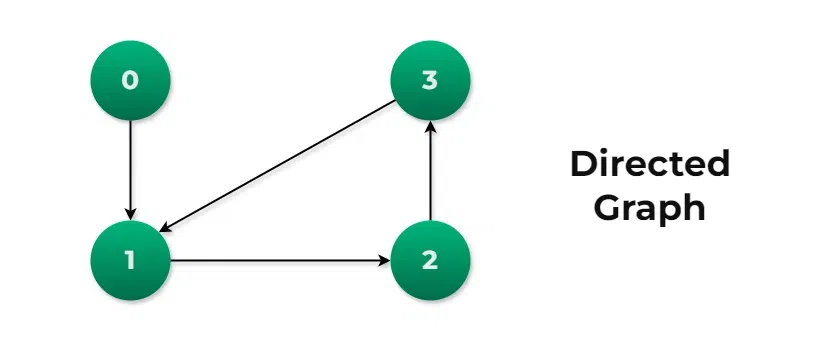Approach: Depth First Search (DFS)

To detect cycles in a directed graph, we can use Depth First Search (DFS) and keep track of the recursion stack to detect back edges, which indicate cycles. The approach is as follows:

1. Create a recursive DFS function that has the following parameters – current vertex, visited array, and recursion stack.
   
2. Mark the current node as visited and also mark the index in the recursion stack.
   
3. Iterate a loop for all the vertices, and for each vertex, call the recursive function if it is not yet visited. This step ensures that if there is a forest of graphs, we are checking each forest.
   
4. In each recursion call, find all the adjacent vertices of the current vertex which are not visited.
   • If an adjacent vertex is already marked in the recursion stack, return true.
   • Otherwise, call the recursive function for that adjacent vertex.
     
5. While returning from the recursion call, unmark the current node from the recursion stack, to represent that the current node is no longer a part of the path being traced.
   
6. If any of the functions returns true, stop the future function calls and return true as the answer.

C Program to Find the Cycle in Directed Graphs

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 100

// Graph structure
struct Graph {
    int numVertices;
    int** adjMatrix;
};

// Create a graph
struct Graph* createGraph(int vertices)
{
    struct Graph* graph
        = (struct Graph*)malloc(sizeof(struct Graph));
    graph->numVertices = vertices;

    graph->adjMatrix
        = (int**)malloc(vertices * sizeof(int*));
    for (int i = 0; i < vertices; i++) {
        graph->adjMatrix[i]
            = (int*)malloc(vertices * sizeof(int));
        for (int j = 0; j < vertices; j++) {
            graph->adjMatrix[i][j] = 0;
        }
    }
    return graph;
}

// Add edge to the graph
void addEdge(struct Graph* graph, int src, int dest)
{
    graph->adjMatrix[src][dest] = 1;
}

// Utility function to detect cycle using DFS
int dfsCycleDetection(struct Graph* graph, int vertex,
                      int* visited, int* recStack)
{
    if (!visited[vertex]) {
        // Mark the current node as visited and add to
        // recursion stack
        visited[vertex] = 1;
        recStack[vertex] = 1;

        // Recur for all vertices adjacent to this vertex
        for (int v = 0; v < graph->numVertices; v++) {
            if (graph->adjMatrix[vertex][v]) {
                if (!visited[v]
                    && dfsCycleDetection(graph, v, visited,
                                         recStack)) {
                    return 1;
                }
                else if (recStack[v]) {
                    return 1;
                }
            }
        }
    }
    recStack[vertex]
        = 0; // Remove the vertex from recursion stack
    return 0;
}

// Function to detect cycle in the graph
int detectCycle(struct Graph* graph)
{
    int* visited
        = (int*)malloc(graph->numVertices * sizeof(int));
    int* recStack
        = (int*)malloc(graph->numVertices * sizeof(int));

    for (int i = 0; i < graph->numVertices; i++) {
        visited[i] = 0;
        recStack[i] = 0;
    }

    for (int i = 0; i < graph->numVertices; i++) {
        if (dfsCycleDetection(graph, i, visited,
                              recStack)) {
            return 1;
        }
    }
    return 0;
}

int main()
{
    struct Graph* graph = createGraph(4);
    addEdge(graph, 0, 1);
    addEdge(graph, 1, 2);
    addEdge(graph, 2, 3);
    addEdge(graph, 3, 1);

    if (detectCycle(graph)) {
        printf("Graph contains cycle\n");
    }
    else {
        printf("Graph doesn't contain cycle\n");
    }

    return 0;
}

Graph contains cycle

Time Complexity: O(V + E), the Time Complexity of this method is the same as the time complexity of DFS traversal which is O(V+E).
Auxiliary Space: O(V). To store the visited and recursion stack O(V) space is needed.

Cycle Detection in Undirected Graphs

In an undirected graph, a cycle is a path that starts and ends at the same vertex, and there is no direction for the edges.

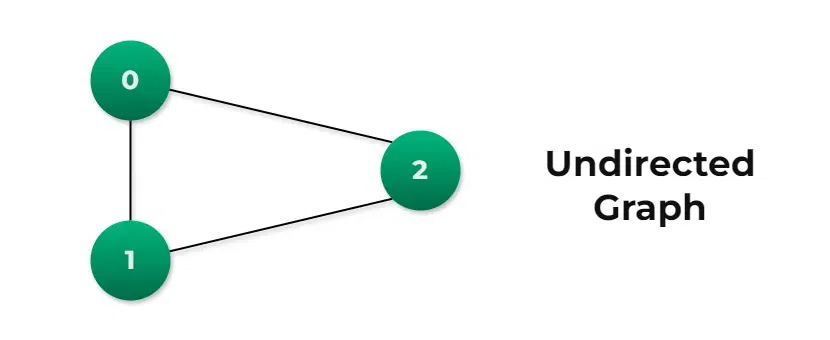Approach: Depth First Search (DFS)

To detect cycles in an undirected graph, we can again use DFS but keep track of the parent node to avoid counting the immediate back edge. The approach is as follows:

1. Create a recursive DFS function that has the following parameters – current vertex, visited array, and parent node.
   
2. Mark the current node as visited.
   
3. Iterate a loop for all the vertices:
   • If an adjacent vertex is not visited, call the recursive function for that adjacent vertex.
   • If an adjacent vertex is visited and not the parent of the current vertex, return true.
     
4. If none of the above conditions are met, return false.

C Program to Find the Cycle in Directed Graphs

#include <stdio.h>
#include <stdlib.h>

// Graph structure for undirected graph
struct Graph {
    int numVertices;
    int** adjMatrix;
};

// Create a graph
struct Graph* createGraph(int vertices)
{
    struct Graph* graph
        = (struct Graph*)malloc(sizeof(struct Graph));
    graph->numVertices = vertices;

    graph->adjMatrix
        = (int**)malloc(vertices * sizeof(int*));
    for (int i = 0; i < vertices; i++) {
        graph->adjMatrix[i]
            = (int*)malloc(vertices * sizeof(int));
        for (int j = 0; j < vertices; j++) {
            graph->adjMatrix[i][j] = 0;
        }
    }
    return graph;
}

// Add edge to the graph
void addEdge(struct Graph* graph, int src, int dest)
{
    graph->adjMatrix[src][dest] = 1;
    graph->adjMatrix[dest][src] = 1;
}

// Utility function to detect cycle using DFS
int dfsCycleDetection(struct Graph* graph, int vertex,
                      int* visited, int parent)
{
    visited[vertex] = 1;

    for (int v = 0; v < graph->numVertices; v++) {
        if (graph->adjMatrix[vertex][v]) {
            if (!visited[v]) {
                if (dfsCycleDetection(graph, v, visited,
                                      vertex)) {
                    return 1;
                }
            }
            else if (v != parent) {
                return 1;
            }
        }
    }
    return 0;
}

// Function to detect cycle in the graph
int detectCycle(struct Graph* graph)
{
    int* visited
        = (int*)malloc(graph->numVertices * sizeof(int));
    for (int i = 0; i < graph->numVertices; i++) {
        visited[i] = 0;
    }

    for (int i = 0; i < graph->numVertices; i++) {
        if (!visited[i]) {
            if (dfsCycleDetection(graph, i, visited, -1)) {
                return 1;
            }
        }
    }
    return 0;
}

int main()
{
    struct Graph* graph = createGraph(3);
    addEdge(graph, 0, 1);
    addEdge(graph, 1, 2);
    addEdge(graph, 2, 0);

    if (detectCycle(graph)) {
        printf("Graph contains cycle\n");
    }
    else {
        printf("Graph doesn't contain cycle\n");
    }

    return 0;
}

Graph contains cycle

Time Complexity: O(V+E), The program does a simple DFS Traversal of the graph which is represented using an adjacency list. So the time complexity is O(V+E).
Auxiliary Space: O(V), To store the visited array O(V) space is required.

Applications

• Deadlock detection: Cycle detection is a feature of operating systems that aids in locating deadlocks in resource allocation graphs.
• Resolving dependencies: Cycle detection in software package management makes sure that no cyclic dependencies exist between packages.
• Network topology: Cycle detection aids in the analysis and optimization of the network architecture in networking.

Related Articles:

• Detect Cycle in a Directed Graph
  
• Detect cycle in an undirected graph
• Depth First Search or DFS for a Graph