|
Quadric surfaces are three-dimensional shapes like ellipsoids, hyperboloids, or paraboloids, described by second-degree equations in three variables. These surfaces have have wide-ranging applications in fields such as physics, engineering, and computer graphics.
This article provides an overview of quadric surfaces, including their definition, equations, types, properties, and applications, serving as a comprehensive guide for understanding these geometric shapes in mathematics and beyond.
What are Quadric Surfaces?
Quadric surfaces, defined by second-degree polynomial equations in three variables, encompass diverse three-dimensional shapes like ellipsoids, spheres, cylinders, cones, paraboloids, and hyperboloids.
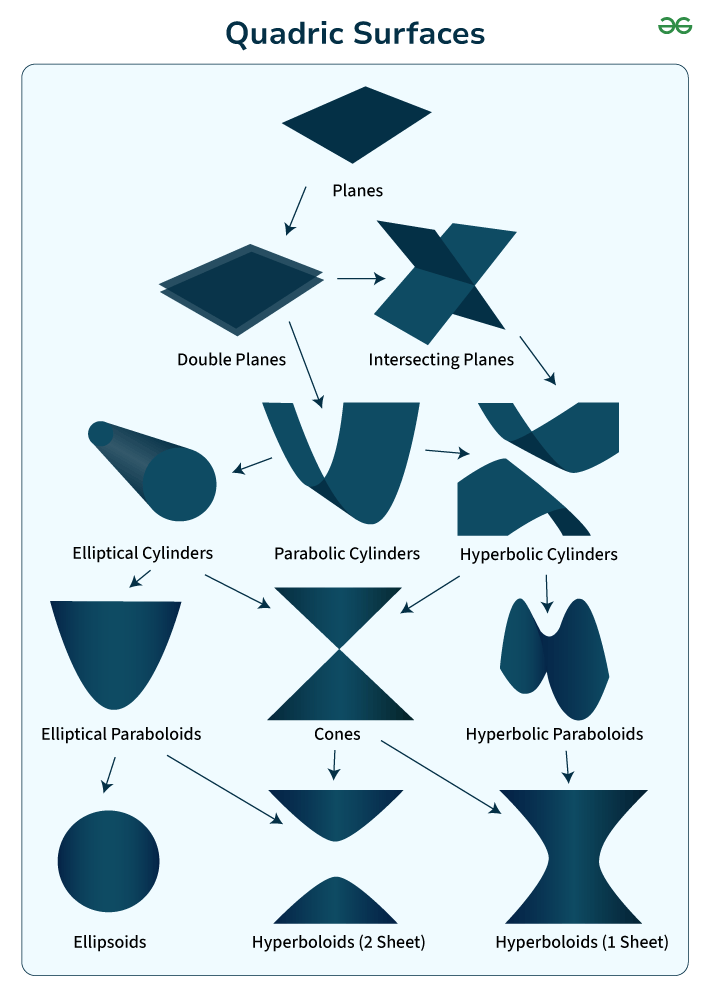 Quadric surfaces Each shape exhibits distinct symmetrical properties and curvature characteristics.
- Ellipsoids resemble stretched or squished spheres, while spheres possess perfect symmetry.
- Cylinders manifest as tube-like structures, and cones feature pointed tips and circular or hyperbolic bases.
- Paraboloids display either elliptic or hyperbolic curvature, while hyperboloids exhibit separate or connected pieces.
Widely used in mathematics, engineering, and computer graphics, quadric surfaces serve as models for real-world objects, from geometric forms to complex structures like antennas and satellite dishes, owing to their mathematical elegance and versatility.
Definition of Quadratic Surface
A quadratic surface is a three-dimensional shape described by an equation of the form Ax² + By² + Cz² + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz + J = 0, where A, B, C, D, E, F, G, H, I, and J are constants.
These surfaces encompass various shapes like ellipsoids, spheres, cylinders, cones, paraboloids, and hyperboloids. They exhibit symmetrical properties and curvature, making them vital in fields like mathematics, engineering, and computer graphics for modeling real-world objects and phenomena.
Equation of Quadric Surface
The equation of a quadric surface in three-dimensional space is typically given by a second-degree polynomial equation in three variables, often written as:
Ax² + By² + Cz² + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz + J = 0
Where A, B, C, D, E, F, G, H, I, and J are constants. This equation represents a wide range of shapes, including ellipsoids, spheres, cylinders, cones, paraboloids, and hyperboloids. The specific coefficients determine the shape and orientation of the quadric surface in space.
| Quadric Surface |
Equation |
Description |
| Ellipsoid |
(x² / a²) + (y² / b²) + (z² / c²) = 1
|
All cross-sections are ellipses. |
| Hyperboloid of One Sheet |
(x² / a²) + (y² / b²) – (z² / c²) = 1
|
Has one connected surface. |
| Hyperboloid of Two Sheets |
(x² / a²) + (y² / b²) – (z² / c²) = – 1
|
Consists of two separate surfaces. |
| Elliptic Paraboloid |
(x² / a²) + (y² / b²) = z/c
|
Shaped like an upward or downward bowl. |
| Hyperbolic Paraboloid |
(x² / a²) – (y² / b²) = z/c
|
Saddle-shaped surface. |
| Elliptic Cone |
(x² / a²) + (y² / b²) – (z² / c²) = 0
|
A double-napped surface. |
| Elliptic Cylinder |
(x² / a²) + (y² / b²) = 1
|
All cross-sections parallel to the z-axis are ellipses. |
| Hyperbolic Cylinder |
(x² / a²) – (y² / b²) = 1
|
All cross-sections parallel to the z-axis are hyperbolas. |
| Parabolic Cylinder |
(x² / a²) = z/c
|
All cross-sections parallel to the y-axis are parabolas. |
Types of Quadric Surfaces
There are various types of quadric surfaces discussed as follows:
| Type |
Description |
| Ellipsoid |
An ellipsoid resembles a stretched or squished sphere, exhibiting three mutually perpendicular axes of symmetry, each with varying lengths.
Its shape is defined by a quadratic equation involving the squares of x, y, and z coordinates, allowing for diverse geometric variations. |
| Sphere |
A sphere is a perfectly symmetrical three-dimensional object where all points on its surface are equidistant from its center, resulting in a round shape.
Its equation involves the sum of squares of x, y, and z coordinates, defining its curvature and symmetry. |
| Cylinder |
Cylinders are tube-like structures with parallel circular bases. Depending on the coefficients in their equations, they can be elliptic or hyperbolic in nature, influencing their cross-sectional shapes and overall geometry.
They play crucial roles in engineering, architecture, and geometric modeling. |
| Cone |
Cones feature a pointed tip (apex) and a base that can either be circular or hyperbolic, depending on the specific parameters in their equations.
Their elegant and distinctive shapes find applications in various fields, from geometry and architecture to physics and engineering. |
| Paraboloid |
Paraboloids are defined by equations with a single quadratic term and no linear terms, resulting in shapes reminiscent of open or closed surfaces.
Depending on the signs of the coefficients, they can be elliptic or hyperbolic in nature, showcasing unique geometric properties and curvatures. |
| Hyperboloid |
Hyperboloids are characterized by equations containing two quadratic terms with opposite signs.
They can manifest as either two separate pieces (two-sheeted hyperboloid) or a single connected piece (one-sheeted hyperboloid), exhibiting complex and intriguing geometric structures with applications in mathematics and physics. |
Applications of Quadric Surfaces
Quadric surfaces have numerous applications across various fields due to their geometric properties and versatility:
In Optics and Engineering
- Paraboloids: Used in satellite dishes and telescopes for focusing incoming electromagnetic waves (such as light or radio waves) to a single point, due to their reflective properties.
- Ellipsoids: Describe the shapes of lenses and mirrors in optics, where they help control the path of light rays.
In Architecture and Design
- Ellipsoids: Often used in architectural design to create aesthetically pleasing shapes for buildings, domes, and structural elements.
- Hyperboloids: Employed in the design of iconic structures like cooling towers and bridges due to their structural strength and unique shape.
In Physics and Mechanics
- Elliptic Cylinders: Describe the shape of pressure vessels and pipes in fluid mechanics, where the cross-section remains constant along the length.
- Parabolic Cylinders: Used in mechanics to model trajectories of particles or projectiles under certain forces, due to their parabolic cross-sections.
Computer Graphics and Animation
- Quadric surfaces are used extensively in computer graphics to model objects in 3D scenes due to their mathematical simplicity and ability to represent a wide variety of shapes.
Mathematical Modeling
- Elliptic Paraboloids and Hyperbolic Paraboloids: Used in mathematical modeling and optimization problems where these surfaces represent constraints or objective functions.
Geology and Geography
- Spheres: Used to model the Earth’s shape in geodesy and for representing geological features such as ore bodies or mineral deposits.
Read More,
Quadric Surface – FAQs
What is a quadric surface?
A quadric surface is a three-dimensional geometric shape described by a second-degree polynomial equation in three variables (x, y, z). It includes various shapes like ellipsoids, spheres, cylinders, cones, paraboloids, and hyperboloids.
What are the common types of quadric surfaces?
Common types of quadric surfaces include ellipsoids, spheres, cylinders, cones, paraboloids, and hyperboloids. Each type has its own unique characteristics and equation.
How are quadric surfaces represented mathematically?
Mathematically, quadric surfaces are represented by equations of the form Ax² + By² + Cz² + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz + J = 0, where A, B, C, D, E, F, G, H, I, and J are constants.
What are the properties of quadric surfaces?
Quadric surfaces can have properties such as symmetry, curvature, and orientation. The specific properties depend on the coefficients in the equation and determine the shape and characteristics of the surface.
What are the applications of quadric surfaces?
Quadric surfaces find applications in various fields, including mathematics, engineering, physics, computer graphics, and architecture. They are used for modeling real-world objects and phenomena, as well as in optimization and design problems.
How do quadric surfaces differ from each other?
Quadric surfaces differ in their shapes, symmetries, and equations. For example, ellipsoids are stretched or compressed spheres, while cones have a pointed tip and a circular or hyperbolic base.
Can quadric surfaces intersect each other?
Yes, quadric surfaces can intersect each other, resulting in complex curves and intersections. The nature of the intersection depends on the specific types of quadric surfaces involved and their orientations.
Are quadric surfaces used in real-world applications?
Yes, quadric surfaces are used extensively in various real-world applications, including architecture, engineering design, computer graphics rendering, physics simulations, and optimization problems.
|

