|
Schwarz-Christoffel transformation is a transformation which is applied in complex analysis for mapping the region of the upper half-plane on the polygonal zones of the plane. This transformation has critically important applications in engineering, and physics and also for solving problems with conformal mappings.
This article is aimed at giving a detailed explanation of Schwarz-Christoffel’s transformation concerning the mathematical basis, the history, characteristics as well as the utility of the model.
What is Schwarz-Christoffel Transformation?Schwarz-Christoffel transformation is one of the conformal mappings that maps the upper half of the complex plane into the interior of a polygon. Mathematically, it is expressed as:
[Tex]f(z) = A + C ∫ Π(z – z_k)^(α_k) dz[/Tex]
where,
- f(z) is the transformed function
- A and C are constants
- zk are the pre-images of the polygon’s vertices in the upper half-plane
- αk are the interior angles of the polygon divided by π minus 1.
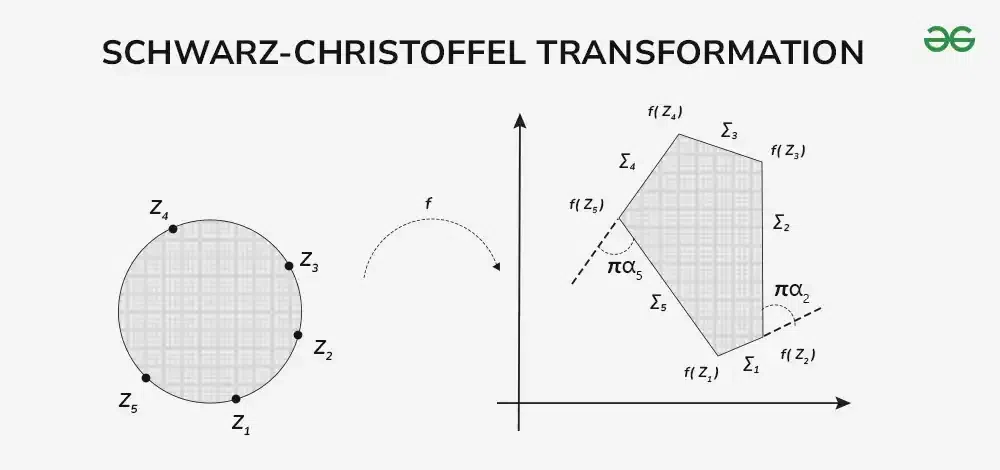 Schwarz-Christoffel Transformation This transformation is essential in solving problems where one needs to map a complex region to a simpler one for easier analysis and problem-solving.
Historical BackgroundSchwarz-Christoffel Transformation was developed in the late 19th century by mathematicians Hermann Schwarz and Elwin Christoffel. Their work on this transformation provided a powerful method for solving complex conformal mapping problems, significantly impacting mathematical analysis and its applications.
Mathematical FormulationMathematical Formulation for Schwarz-Christoffel Transformation is:
Integral Formulation
The integral form of the Schwarz-Christoffel transformation is given by:
[Tex]f(z) = A + C ∫ Π(z – z_k)^{(α_k)} dz[/Tex]
Constants and Parameters:
- A:Complex constant representing translation.
- C: Scaling constant.
- zk: Pre-images of the vertices of the polygon in the upper half-plane.
- αk: Angles of the polygon vertices, given by α_k = θk/π − 1, where θk is the interior angle at the k-th vertex.
Mapping PropertiesSchwarz-Christoffel transformation maps the upper half-plane onto the interior of a polygon. Key properties include:
- Conformal Mapping: Preserves angles at which curves intersect.
- Polygonal Mapping: Maps the real axis to the boundary of a polygon.
- Vertex Correspondence: The points zk in the upper half-plane correspond to the vertices of the polygon.
Applications of Schwarz-Christoffel transformationThe applications of Schwarz-Christoffel transformation are:
- Fluid Dynamics: Used to solve potential flow problems around polygonal obstacles.
- Electrostatics: Helps in determining electric field distributions in polygonal regions.
- Aerodynamics: Assists in mapping airfoil shapes for aerodynamic analysis.
- Structural Mechanics: Applied in stress analysis of polygonal structures.
- Heat Transfer: Used in solving heat distribution problems in polygonal domains.
- Complex Analysis: Provides solutions to complex integration problems in polygonal regions.
Numerical Methods for Solving Schwarz-Christoffel TransformationNumerical techniques for solving the Schwarz-Christoffel transformation involve discretizing the integral and solving it using computational algorithms. These methods are crucial for handling complex polygonal mappings that are challenging to solve analytically.
- Computational Solutions: Tools like MATLAB and specialized software can compute the Schwarz-Christoffel transformation for complex shapes, enabling practical applications in various fields.
Generalizations of Schwarz-Christoffel TransformationGeneralizations of the Schwarz-Christoffel transformation include mapping to regions with curved boundaries and regions with more complex topologies. These advanced mappings require modifications to the integral formulation to accommodate the additional complexity.
Examples on Schwarz-Christoffel TransformationExample 1: Map the upper half-plane to the interior of a rectangle with vertices at (0,0), (1,0), (1,1), and (0,1).
Solution:
Identify the pre-images z1, z2, z3, z4 on the real axis. Without loss of generality, we can choose the pre-images as z1 = −1, z2 = 0, z3 = 1, and z4 = ∞.
Set up the integral form:
[Tex]f(z) = A + C ∫ (z – z_1)^(-1/2) (z – z_2)^(-1/2) (z – z_3)^(-1/2) dz[/Tex]
Substituting z1=−1, z2=0, and z3=1:
[Tex]f(z) = A + C ∫ (z + 1)^(-1/2) z^(-1/2) (z – 1)^(-1/2) dz[/Tex]
To solve the integral, we recognize that the integrand can be simplified using the change of variables method. Let z=sin2(θ), so dz=2sin(θ)cos(θ)dθ. The integral becomes:
[Tex]f(z) = A + C ∫ (sin^2(θ) + 1)^(-1/2) (sin^2(θ))^(-1/2) (sin^2(θ) – 1)^(-1/2) 2sin(θ)cos(θ) dθ[/Tex]
Simplifying further and solving the integral, we get:
After evaluating the integral, we obtain the mapping function. The exact evaluation of the constants A and C will depend on boundary conditions and the specific geometry of the rectangle.
Use boundary conditions to solve for A and C. For a standard rectangle mapping:
Therefore, the mapping function becomes:
[Tex]f(z) = ∫ (z + 1)^(-1/2) z^(-1/2) (z – 1)^(-1/2) dz[/Tex]
This integral can be solved numerically to provide the exact mapping from the upper half-plane to the interior of the rectangle.
Example 2: Map the upper half-plane to the interior of a pentagon with specific vertex angles.
Solution:
Determine the angles and corresponding αk values. Let the interior angles of the pentagon be θ1, θ2, θ3, θ4, θ5. The corresponding αk values are:
αk = θk / (π – 1)
For a regular pentagon, each interior angle is 3?/5. Therefore:
αk = (3/5) – 1 = -2/5
Identify the pre-images z1, z2, z3, z4, z5 on the real axis. We can choose these pre-images as z1=−1, z2 =−1/2, z3 =0, z4 =1/2, and z5 =1.
Set up the integral form:
[Tex]f(z) = A + C ∫ (z – z_1)^(α_1) (z – z_2)^(α_2) (z – z_3)^(α_3) (z – z_4)^(α_4) (z – z_5)^(α_5) dz[/Tex]
Substituting αk =−2/5:
[Tex]f(z) = A + C ∫ (z + 1)^(-2/5) (z + 1/2)^(-2/5) z^(-2/5) (z – 1/2)^(-2/5) (z – 1)^(-2/5) dz[/Tex]
This integral can be quite complex and typically requires numerical evaluation or approximation methods. Using software tools, we can numerically evaluate the integral to find the exact mapping function.
Solve for the constants A and C using boundary conditions. For example, by setting the centroid of the pentagon to map to z=0 and ensuring proper scaling and rotation, we can find suitable values for A and C.
Therefore, the mapping function becomes:
[Tex]f(z) = ∫ (z + 1)^(-2/5) (z + 1/2)^(-2/5) z^(-2/5) (z – 1/2)^(-2/5) (z – 1)^(-2/5) dz[/Tex]
This integral, once solved, will provide the mapping from the upper half-plane to the interior of the pentagon.
ConclusionSchwarz-Christoffel transformation is a fundamental tool in complex analysis, providing a method to map the upper half-plane to polygonal regions. Its mathematical formulation, involving integrals and specific constants, allows for precise conformal mappings. The transformation has diverse applications across engineering and physics, particularly in areas requiring complex shape analysis.
Advanced numerical methods and generalizations further extend their utility to more intricate mapping problems. Understanding and applying the Schwarz-Christoffel transformation equips students and professionals with a powerful technique for solving a wide range of practical and theoretical problems.
FAQs on Schwarz-Christoffel TransformationWhat is Schwarz-Christoffel Transformation Used For?It is utilized to describe the conformal transformation which is used to map the upper half of the plane to the region enclosed within some polygon in the complex plane.
What are Limitations of Schwarz-Christoffel Transformation?It mainly applies to polygonal regions and can be complex to calculate for polygons with many sides.
Can Schwarz-Christoffel Transformation Map Non-Polygonal Regions?No, it is specifically designed for mapping to polygonal regions.
How is Transformation Applied in Fluid Dynamics?Schwarz-Christoffel Transformation helps in solving problems involving fluid flow around polygonal obstacles or in polygonal channels.
What do Conformal Maps Show Most Accurately?Conformal Maps show angles accurately, preserving the shape of infinitesimally small figures.
|

