|
In Natural Language Processing (NLP), the advent of the Transformer architecture has markedly changed how machines understand and generate human language. At the heart of this innovation is the self-attention mechanism, which crucially enables the model to weigh the importance of different words within a sentence regardless of their positional distances. However, self-attention mechanisms cannot inherently process the order of words, a fundamental aspect for understanding contextual meanings in sentences. Positional embeddings are introduced to address this limitation, providing vital context that enhances the model’s understanding of text.
Understanding the Self-Attention MechanismSelf-attention is a mechanism allowing each word in a sentence to interact (‘attend’) with every other word, capturing dependencies that are crucial for understanding the text fully. This mechanism computes a weighted sum of input embeddings, where the weights (attention scores) are determined by the similarity between words.
Key Steps in Self-Attention:- Calculating Queries, Keys, and Values: For each token in the input, three vectors are derived using learned weight matrices—Queries (Q), Keys (K), and Values (V). These vectors are projected into a lower-dimensional space for efficient processing.
- Computing Attention Scores: Attention scores are calculated by taking the dot product of the Query vector of each token with all Key vectors, resulting in scores that represent the relevance or similarity between tokens. A softmax function then normalizes these scores to ensure they sum to 1, representing probabilities.
- Generating Output: The output vector for each token is computed as a weighted sum of all Value vectors, with weights given by the attention scores. This step combines the information from different parts of the input sequence according to the computed relevancies.
Despite its effectiveness, self-attention views words as sets of features without regard for their sequential order, which leads to a potential loss of context inherent in the sequence of words.
Role of Positional EmbeddingsPositional embeddings are crucial because, without them, the model would treat permutations of the same set of words as identical. For example, “The quick brown fox” would be indistinguishable from “fox brown quick The” in the eyes of a purely self-attentional model. Positional embeddings resolve this by providing a unique representation for each position in the sequence, allowing the model to differentiate “The” as the first word from “fox” as the last.
Mathematical FormulationEach word in a sequence is associated with a positional embedding vector:
- Positional Embedding for Position i: [Tex]PE_i[/Tex] is defined using sine and cosine functions of different frequencies:
- [Tex]\text{PE}(\text{pos}, 2i) = \sin\left(\frac{\text{pos}}{10000^{\frac{2i}{d_{\text{model}}}}}\right)[/Tex]
- [Tex]\text{PE}(\text{pos}, 2i + 1) = \cos\left(\frac{\text{pos}}{10000^{\frac{2i}{d_{\text{model}}}}}\right)[/Tex]
These embeddings are added to the word embeddings to provide information about the relative or absolute position of the tokens in the sequence.
Implementation of Positional Encoding for Transformers The provided Python implementation details a module called PositionalEncoding, which is built using PyTorch, a popular deep learning library. This module generates positional embeddings for tokens in a sequence, which are crucial for models like Transformers that need to maintain information about the order of elements in sequences they process.
Step 1: Positional Encoding Generation The code dynamically generates a matrix of positional encodings based on the length of sequences (max_len) and the dimensionality of each token’s embedding (d_model). This matrix incorporates sinusoidal functions of different frequencies, which helps the model to understand and retain the position of each token within the sequence.
Python
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000):
super(PositionalEncoding, self).__init__()
# Create a matrix of shape (max_len, d_model)
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-np.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0).transpose(0, 1)
self.register_buffer('pe', pe)
def forward(self, x):
return x + self.pe[:x.size(0), :]
# Hyperparameters
d_model = 512
max_len = 100
# Initialize Positional Encoding
pos_encoding = PositionalEncoding(d_model, max_len)
Step 2: Visualize Positional embeddings generated by the ‘PositionalEncoding’
Python
# Extract the positional embeddings
pe = pos_encoding.pe.squeeze(1).numpy()
# Plot positional embeddings for different dimensions
plt.figure(figsize=(15, 10))
for i in range(0, d_model, 64): # Plot every 64th dimension
plt.plot(pe[:, i], label=f"Dimension {i}")
plt.title("Positional Embeddings for Different Dimensions")
plt.xlabel("Position")
plt.ylabel("Embedding Value")
plt.legend()
plt.show()
Output:
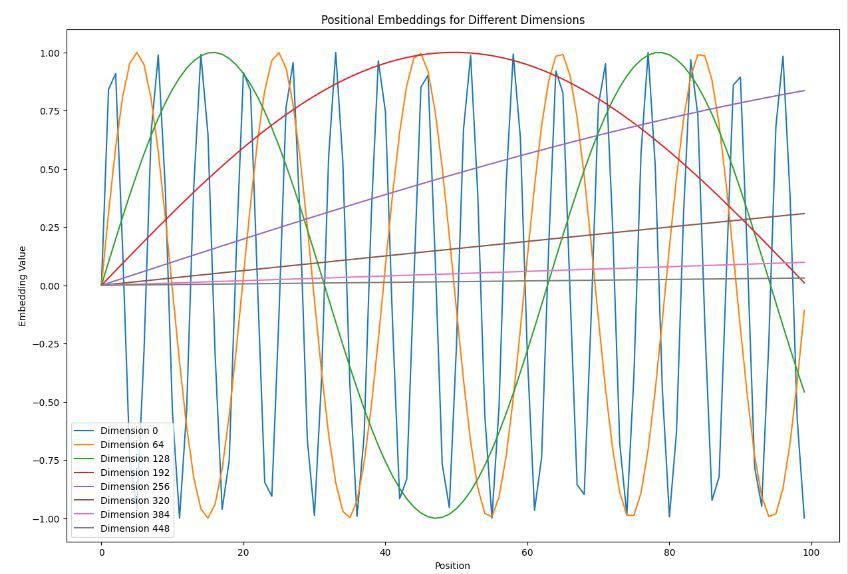 This visualization serves several purposes:
- Understanding Variability: It shows how the values of positional embeddings change across different positions in the sequence, reflecting how the Transformer model might use these variations to understand the order of words or tokens in the input.
- Frequency Analysis: By observing the waveforms of embeddings across positions, one can see how different frequencies are encoded by different dimensions. Lower-index dimensions often encode lower-frequency signals, while higher-index dimensions encode higher-frequency signals. This property helps the model capture patterns at various granularities.
- Model Diagnostics and Insight: Developers and researchers can use such plots to verify that positional embeddings are correctly implemented and behaving as expected. It also provides insights into the model’s ability to differentiate between positions, which is crucial for tasks that rely heavily on the order of elements, like language processing.
Step 3: Visualize the Heatmap of Positional Encodings
Python
# Heatmap of positional embeddings
plt.figure(figsize=(15, 5))
plt.imshow(pe.T, cmap='viridis', aspect='auto')
plt.title("Heatmap of Positional Embeddings")
plt.xlabel("Position")
plt.ylabel("Embedding Dimension")
plt.colorbar()
plt.show()
Output:
.png)
Shows how the values of positional encodings change across different positions and embedding dimensions. The patterns observed (typically wave-like patterns due to sine and cosine functions) provide insights into how the model might distinguish between different positions within a sequence.
ConclusionPositional embeddings play a crucial role in the self-attention mechanism by encoding the order of words in a sequence. This enhances the model’s ability to understand context and relationships between words, making it a powerful tool in NLP. Through our PyTorch implementation and visualization, we have seen how these embeddings are generated and integrated into the Transformer model.
Working of Positional Embeddings in Self Attention-FAQsWhy do we use sine and cosine functions for positional embeddings?Sine and cosine functions provide a smooth, periodic way to encode positional information, allowing the model to generalize to varying sequence lengths.
Can we use learned positional embeddings instead of fixed ones?Yes, some models use learned positional embeddings, which can be trained along with the rest of the model parameters.
Are there other functions used for positional embeddings?Yes, there are other functions rather than sine and cosine, Fourier Series, Exponential Decaying can also be used or learnable embeddings can also be used for representing positions.
|


.png)