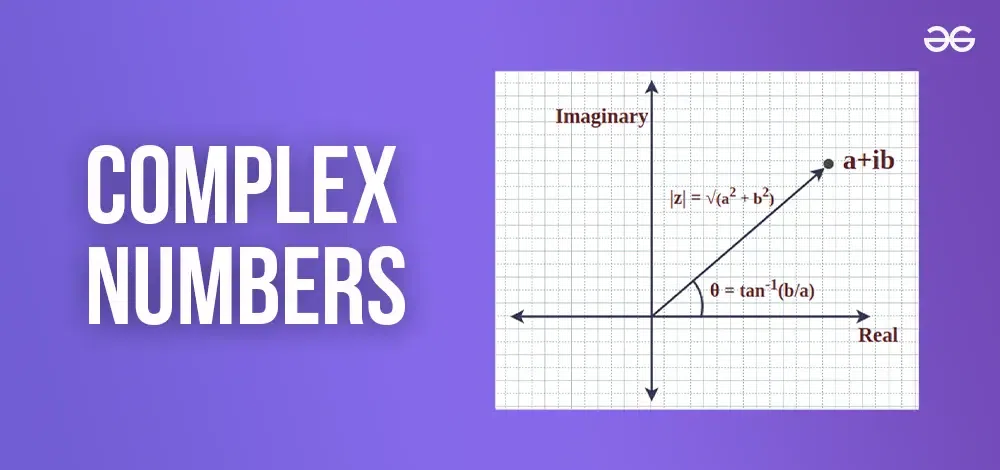
Graphing complex numbers is an interesting aspect of mathematics that combines algebra and geometry to provide a visual representation of complex equations. Graphing complex numbers is an effective way of providing a graphical representation of complex numbers which are unique mathematical entities. The complex numbers that contain real and imaginary parts are drawn by complex planes similar to two-dimensional Cartesian planes.

By Plotting complex numbers, we can see their relationships and interactions, enhancing comprehension and practical problem-solving skills.

This article defines the methods and significance of graphing complex numbers ( plotting complex numbers on graph) on the complex plane, also illustrates how the real and imaginary components come together to form a complete picture.

What Are Complex Numbers?

Complex numbers are numbers that consist of two parts: a real part and an imaginary part. Complex numbers extend the idea of one-dimensional real numbers to the two-dimensional complex plane, allowing for the solution of equations that have no real solutions. They are used in various fields such as engineering, physics, and applied mathematics to model and solve problems involving oscillations, waves, and other phenomena that cannot be adequately described using only real numbers.

Complex Numbers

A complex number z is defined as:

[Tex]z = a + bi[/Tex]

where,

• a and b are Real Numbers
• i is Iota

[Tex]i^2 = −1[/Tex]

In this notation, a is called the real part of z (denoted as R(z)), and b is called the imaginary part (denoted as I(z)). Thus, for a complex number z:

[Tex]R(z) = a[/Tex]

[Tex]I(z) = b[/Tex]

[Tex]z = R(z) +I(z)i[/Tex]

Properties of Complex Numbers

The basic properties of complex numbers are as follows:

• Addition: The sum of two complex numbers [Tex]z1 =a+bi[/Tex] and [Tex]z2 =c+di[/Tex] is given by: [Tex]z_1 + z_2 = (a + c) + (b + d)i[/Tex]

• Subtraction: The difference between two complex numbers z₁ and z₂ is: [Tex]z_1 – z_2 = (a – c) + (b – d)i[/Tex]

• Multiplication: The product of z₁ and z₂ is: [Tex]z_1 \cdot z_2 = (ac – bd) + (ad + bc)i[/Tex]

• Division: The quotient of z₁ divided by z₂ is: [Tex]\frac{z_1}{z_2} = \frac{(a + bi)(c – di)}{c^2 + d^2} = \frac{ac + bd}{c^2 + d^2} + \frac{bc – ad}{c^2 + d^2}i[/Tex]

• Conjugate: The conjugate of z is denoted as and [Tex]\overline{z}[/Tex] is given by: [Tex]\overline{z} = a – bi[/Tex]

• Modulus: The modulus of z, denoted as ∣z∣, is: |z| = [Tex]\sqrt{a^2 + b^2}[/Tex]

Graphing Complex Numbers

Complex number can be plotted on a graph in two ways that includes:

• Cartesian Representation of Complex Numbers
• Polar Representation of Complex Numbers

Cartesian Representation of Complex Numbers

The Cartesian form of complex numbers enables, the complex numbers to be represented on a two-dimensional plane whose coordinates are normally referred to as the real axis and the imaginary axis.

Plotting Complex Numbers on Complex Plane

Complex plane is one of the planes that comprise two dimensions whereby each complex number has its point in the plane. The x-axis or the horizontal axis is called the real axis here it shows the real value of the number whereas the y-axis or vertical axis is known as the imaginary axis which shows the imaginary part of the number.

For a complex number z = a + bi:

• Real axis: Corresponds to a
• Imaginary axis: Corresponds to b

Plotting Complex Numbers on Complex Plane

Steps to Plot Complex Numbers

Identify the Components: Determine the real part a and the imaginary part b of the complex number z.

• z = 2 + 3i

Locate on Real Axis: Plot the value a on the horizontal axis.

• Real part a = 2

Locate on Imaginary Axis: Plot the value b on the vertical axis.

• Imaginary part b = 3

Mark the Point: The point where these values intersect is the graphical representation of the complex number.

• Point (2, 3)

Plot Multiple Numbers: Repeat the above steps for additional complex numbers to visualize their relationships.

Polar Representation of Complex Numbers

Polar representation of complex numbers on the graph involves expressing such numbers in terms of their magnitude and angle of orientation with the positive real axis as another form of coordinate system.

Conversion Between Cartesian and Polar Form

The conversion between Cartesian form [Tex]z = a + bi[/Tex] and polar form [Tex]z = r(cosθ + isinθ)[/Tex] involves the following formulas:

From Cartesian to Polar:

[Tex]r = \sqrt{a^2 + b^2} \theta = \tan^{-1}\left(\frac{b}{a}\right)[/Tex]

From Polar to Cartesian:

[Tex]a = r \cos \theta b = r \sin \theta[/Tex]

Example: Given [Tex]z = 3 + 4i[/Tex]:

[Tex]r = \sqrt{3^2 + 4^2} = 5 \\ \theta = \tan^{-1}\left(\frac{4}{3}\right) \approx 53.13^\circ[/Tex]

Plotting Complex Numbers in Polar Coordinates

Determine Magnitude and Angle: Compute the magnitude r and angle θ.

Plot the Point: From the origin, measure the angle θ counterclockwise and mark the point at distance r.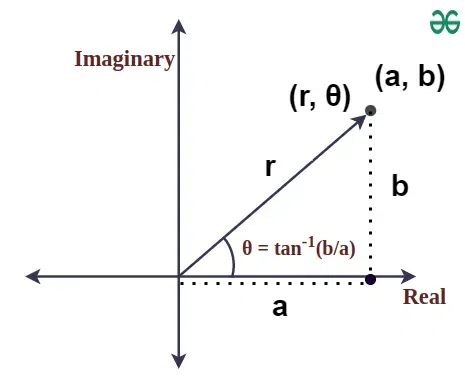

Plotting Complex Numbers in Polar Coordinates

Example : Plot the complex numbers Z_{1 =} 5 + 3i on Graph.

Example : Plot the complex numbers Z_{2 =} 5(cos60^∘ +isin60^∘) on Graph.

Operations on Complex Plane

Performing calculations on complex numbers is as easy as moving points on the complex plane and thus eases the understanding of their algebraic transformations.

Example on Addition and Subtraction of complex number

Graphical Interpretation: Adding or subtracting complex numbers corresponds to vector addition or subtraction on the complex plane.

Example: For z₁ = 3+4i and z₂ = 1+2i:

[Tex]z_1 + z_2~=~(3 + 1) + (4 + 2)i~=~4 + 6i\\ z_1 – z_2~=~(3 – 1) + (4 – 2)i~=~~2 + 2i[/Tex]

Example on Multiplication and Division of complex number

Polar Form Multiplication: Multiplying complex numbers in polar form involves multiplying their magnitudes and adding their angles.

[Tex]z_1 \cdot z_2 = r_1 r_2 \left( \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2) \right)[/Tex]

Polar Form Division: Dividing complex numbers involves dividing their magnitudes and subtracting their angles.

[Tex]\frac{z_1}{z_2} = \frac{r_1}{r_2} \left( \cos(\theta_1 – \theta_2) + i \sin(\theta_1 – \theta_2) \right)[/Tex]

Example: Given z₁ = 5(cos45^∘ +isin45°) and z₂ = 2(cos30^∘ +isin30^∘) perform multiplication and division of z1 and z2.

[Tex]z1.z2 = {5(cos45∘ +isin45°)}.{2(cos30∘ +isin30∘)}[/Tex]

[Tex]z1.z2 = 10{(cos 75∘) + i(sin 75∘)}[/Tex]

[Tex]z1/z2 = {5(cos45∘ +isin45°)}/{2(cos30∘ +isin30∘)}[/Tex]

[Tex]z1/z2 = 5/2{(cos 15∘) + i(sin 15∘)}[/Tex]

Read More:

• Euler’s Formula
• De Moivre’s Formula
• Complex Plane
• Conjugate of Complex Number

Applications of Graphing Complex Numbers

The applications of Graphing Complex numbers are as follows:

• Electrical Engineering: Used in analyzing AC circuits and phasor diagrams.

• Quantum Physics: Essential for describing quantum states and wave functions.

• Signal Processing: Applied in Fourier transforms and frequency domain analysis.

• Control Systems: Utilized in system stability and feedback loop analysis.

• Fluid Dynamics: Employed in potential flow and complex potential functions.

Conclusion

Understanding and graphing complex numbers provide deep insights into various mathematical and real-world applications. Through Cartesian and polar representations, complex numbers can be visually analyzed, facilitating operations and comprehension. These concepts are indispensable in fields such as engineering, physics, and signal processing, highlighting the importance of mastering complex number graphing techniques.

Graphing Complex Numbers- FAQs

How to Plot Complex Number on Complex Plane?

Make a graph of the complex number [Tex](a + ib)[/Tex] by making it on a coordinate axis such that ‘a’ is located on the x-axis and ‘b’ on the y-axis.

How can Complex Numbers also be Represented?

Complex numbers can be represented in polar form as [Tex]r(cos θ + isin θ) [/Tex]or [Tex]re^{iθ}[/Tex] , where r is the magnitude and θ is the angle between them.

What is Real Part of Complex Number Plotted on Graph?

Real part is plotted on the coordinate on the x-axis.