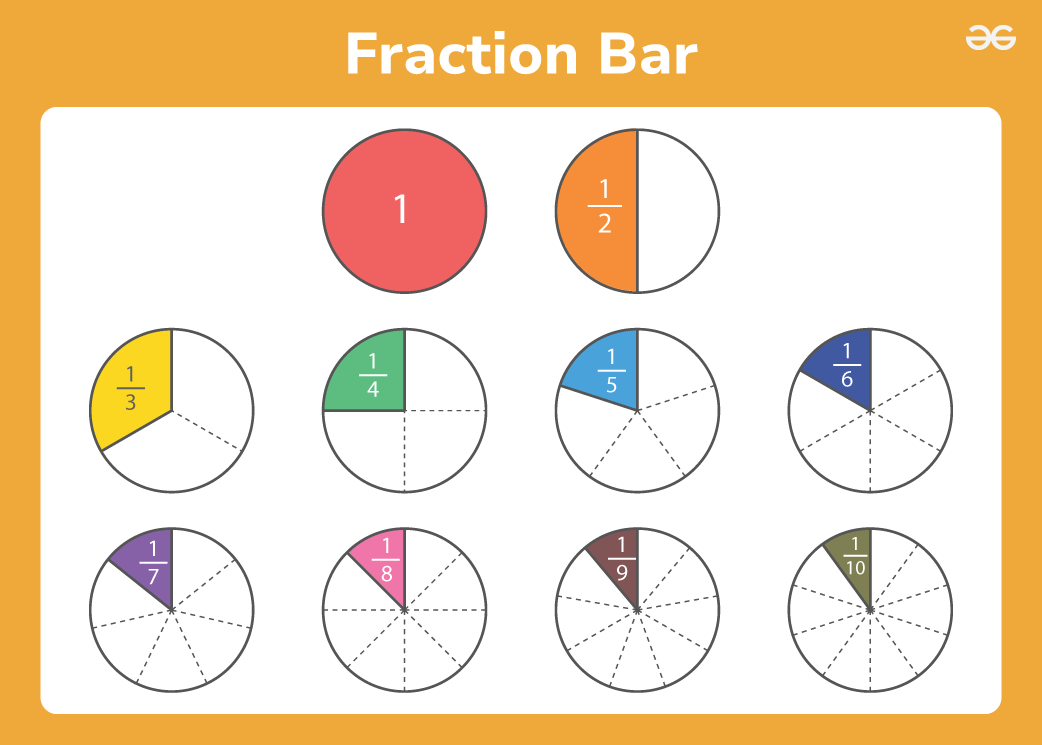
Fraction bars are visual and hands-on tools used to teach and understand fractions. They provide a simple way to see the size of different fractions and how they relate to each other. These are especially helpful in elementary and middle school education for introducing and reinforcing concepts of fractions.

In this article, we will understand fraction bars and solve some questions with fraction bars.

What are Fraction Bars?

In mathematics, a fraction bar is a visual tool that helps compare fractions and perform fraction operations.

Fraction bars or strips represent a part-to-whole relationship. Each segment of a fraction bar represents one part of the whole. This is why it is called a part-to-whole representation.

A fraction bar is divided into equal parts, and the number of shaded parts shows the fraction being represented.

Definition of Fraction Bars

A fraction bar is a visual tool used in mathematics to represent fractions. It consists of a bar divided into equal segments, where each segment represents a part of the whole. This helps in comparing fractions and performing operations with them.

Fraction strips are rectangular pieces of paper that are divided into equal parts to represent different fractions. Each strip is usually marked with fractional values such as 1/2, 1/3, 1/4, and so on. They are often color-coded to make it easier to differentiate between various fractions.

Comparing Fractions using Fraction Bars

Fraction strips or fraction bars are a visual and interactive tool that help students understand and compare the sizes of different fractions. They are helpful in comparing fractions in an easy way.

Here are few examples for the same:

Example: Comparing 1/2 and 2/3

Solution:

• Strips: Take the 1/2 strip and the 2/3 strip.
• Align Strips: Place both strips side by side, starting at the same point.
• Compare Lengths: Notice that the 2/3 strip is longer than the 1/2 strip, showing that 2/3 is greater than 1/2.

Example: Comparing 3/4 and 5/6

Solution:

• Select Strips: Take the 3/4 strip and the 5/6 strip.
• Align Strips: Place both strips side by side, starting at the same point.
• Compare Lengths: The 5/6 strip will be slightly longer than the 3/4 strip, indicating that 5/6 is greater than 3/4.

Algebraic Expressions with Fraction Bars

When solving an algebraic expressions that include fraction bars, it is important to consider these bars as grouping symbols, similar to parentheses. Some key points to use while solving algebraic expressions with fraction bars are:

Invisible Parentheses

Both the numerator and the denominator of a fraction can be considered to have invisible parentheses around them. Suppose, in an algebraic expression [Tex]\frac{3 + 3}{4 \times 1}[/Tex] there is no visible parentheses. Hence, while solving the fraction, first all operations of the numerator and the denominator should be solved separately.

Like in the fraction given above,

numerator = 3 +3 = 6

denominator = 4 × 1 = 4

The new fraction becomes 6/4

Now, as the invisible parentheses of numberator and denominator are solved, we can solve the new fraction as a whole,

6/4 = 3/2

Order of Operations- PEMDAS

PEMDAS expands to parentheses, exponents, multiplication, division, addition and subtraction. Order of operations means, solving the algebraic expression using PEMDAS rule starting with operation P for parentheses then E, M, D, A, and S.

Suppose in an algebraic equation 3+4×2-5, we have to use PEMDAS rule.

• P (parentheses): The expression has no parentheses.
• E (exponents): The expression has no exponents.
• M (multiplication): The expression has 4×2, therefore on solving this first we get 8. and the new expression becomes 3+8-5.
• D (division): the expression has no division sign.
• A (addition): The expression has 3+8, therefor on solving this operation we get, 11 and the new expression becomes 11-5
• S (subtraction): The last of PEMDAS is subtraction. Hence, 11-5 = 6.

This is how PEMDAS is used to solve an algebraic expressions.

NOTE: If, in an algebraic expression there are more than one brackets or parentheses, then solve the innermost parentheses first.

Parentheses in Numerator or Denominator

If there are actual parentheses within the numerator or denominator, those operations take precedence over the fraction bar. Solve everything inside these parentheses before addressing the fraction.

Parentheses Outside the Fraction

If there are parentheses outside of the fraction, the fraction bar itself takes precedence over the operations inside these outer parentheses.

Example of Algebraic Expressions with Fraction Bars

Example: Given: [Tex]\frac{(3 + 2) \times 4}{(1 + 1) \times 2}[/Tex]

Solution:

First we will simplify the parentheses of numerator and denominator.

[Tex]\frac{5 \times 4}{2 \times 2}[/Tex]

Now perform the operations in numerator and denominator

Numerator= 5 × 4 = 20

Denominator = 2 × 2 = 4

Now on simplifying the fraction, we get:

20/4 = 5

Benefits of Using Fraction Bars

• Visual Learning: Fraction strips provide a visual representation of fractions, making abstract concepts more concrete.

• Comparison: They allow students to compare fractions easily, helping them understand which fractions are larger or smaller.

• Addition and Subtraction: Fraction strips can be used to visually demonstrate the process of adding and subtracting fractions.

• Equivalency: They help in understanding equivalent fractions, showing how different fractions can represent the same part of a whole.

• Interactive Learning: Using fraction strips in activities and games engages students and enhances their learning experience.

Read More:

• Fraction
• Comparing Fractions
• Decimal Fractions

Solved Examples on Fraction Bars

Example 1: Simplify the expression [Tex]\frac{5 \times (2 + 3)}{4 – 1}[/Tex].

Solution:

According to PEMDAS, we will first solve paranthesis 2+3 =5

Now we have no exponents, so we will solve multiplication operation: 5 × 5

As noted in the article above, we must the numerator and denominator must be considered as having invisible parenteses. Therefore, we will solve the denominator first before solving the division operation in the given expression.

Now we have 5 × 5 / 4-1

= 25/5

=5

Example 2: Comparing 7/10 and 4/5

Solution:

• Select Strips: Choose the fraction strips representing 7/10 and 4/5.
• Align Strips: Place both strips side by side, starting at the same point.
• Visual Comparison: Observe the lengths of the strips. You will see that the strip representing 4/5 is longer than the strip representing 7/10.

This comparison visually demonstrates that 4/5 is greater than 7/10.

Example 3: If a fraction bar is divided into 6 equal parts and 3 parts are shaded, what fraction of the bar is shaded?

Solution:

If a fraction bar is divided into 6 equal parts and 3 parts are shaded, the fraction of the bar that is shaded is 3/6​ or 1/2​.

Example 4: A rectangle is divided into 8 equal parts by a fraction bar. If 5 of these parts are shaded, what fraction of the rectangle is shaded?

Solution:

As the total parts we have in the rectangle are 8, so the denominator is 8.

The shaded part in the rectangles are 5. Therefore the numerator is 5.

The fraction so becomes and represented in fraction bar as 5/8.

Fraction Bars Worksheet: Unsolved

FAQs on Fraction Bars

What are fraction bars?

Fraction bars are the horizontal lines used to separate the numerator from the denominator. This fraction bar shows the number in division form.

What are Fraction strips?

Fraction strips are visual aids used in mathematics education to represent fractions. They consist of rectangular strips divided into equal parts, with each part representing a fraction of a whole.

What are fraction bars called?

Fraction bars are also known as division bars or vinculum. They are also known as Fraction Strips.

What is 0.5 bar fraction?

The fraction representation of 0.5 is 1/2.

Why are fraction bars important?

Fraction bars are important because they visually represent the division operation in fractions which makes it easier to understand and compare different fractional quantities.

What is an example of a fraction bar?

3/4 is an example of a fraction bar, where the fraction bar separates the numerator 3 and the denominator.

Who was the first to use a fraction bar?

Leonhard Euler was the first person to use a fraction bar.

What is the difference between a fraction bar and a number line?

The difference between both is that a fraction bar represents the division of one quantity by another, while a number line represents the continuum of numbers from one point to another.