|
|
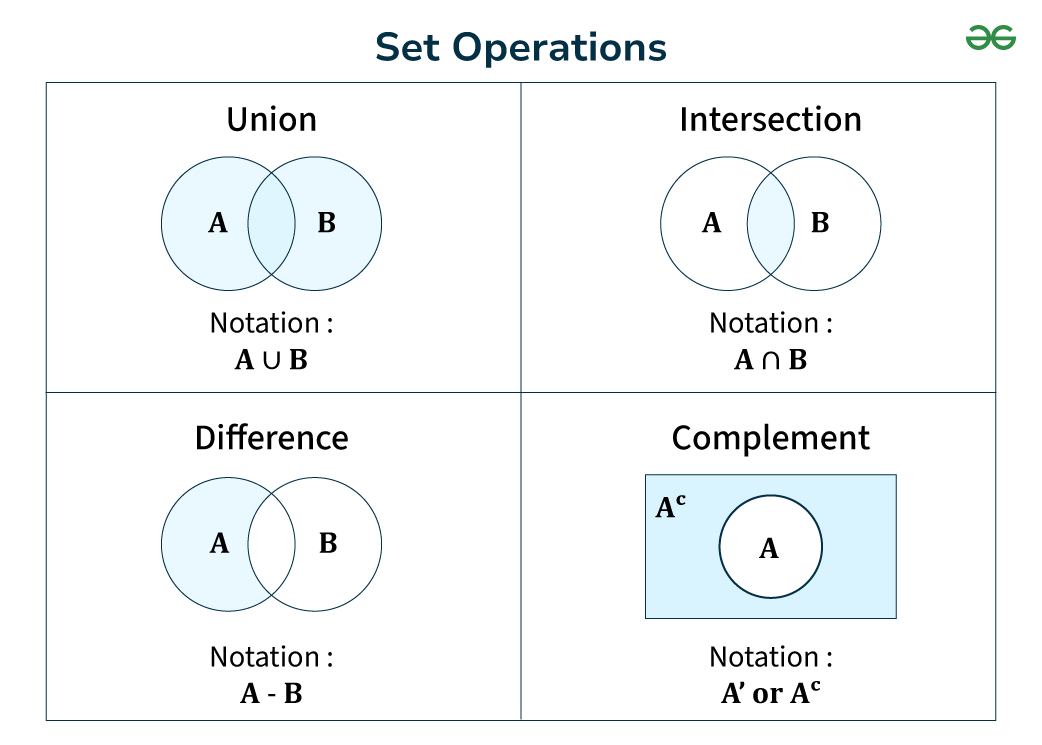
When studying set theory, having a good understanding of the various operations on sets is crucial and an effective way to deepen this understanding is by working through practice questions on operations on sets. These Practice Questions on Operations on Sets will help to reinforce the fundamental concepts of the Set theory. In set theory, there are three major types of operations performed on sets:
Other set operations include symmetric differences. In this article, we will discuss about various operations on sets, formulas for those operations along with some practice Questions on Operations on Sets. Table of Content Formulas on Operations on Sets Operations on Set The table below represents the formulas for different operations on sets.
Practice Questions on Operations on Sets – SolvedThese practice questions on operations on sets are designed to enhance your understanding of key concepts such as union, intersection, difference, and complement. 1. Find the union of set A and B given that set A = {2, 4, 6} and set B = {4, 10}.
2. Find the intersection of set X and Y given X = {5, 9, 10, 15} and Y = {4, 5, 12}.
3. Find the complement of set P given the universal set U = {10, 20, 30, 40, 50, 60} and P = {20}.
4. Find the set difference of sets C and D given that C = {1, 4, 7} and D = {4, 8}
5. Find the power set of the set A = {2, 7}
6. What are the number of elements in the union of two sets P and Q with number of elements 5, 6 respectively. Also, the number of common elements in both sets is 2.
7. Find the number of elements in the intersection of two sets given the number of elements of sets U and V are 8 and 9 and the number of elements in their union is 13.
Practice Questions on Operations on Sets – Unsolved1. Find the union of set A and B given that set A = {1, 2, 5} and set B = {7, 9}. 2. Find the intersection of set X and Y given X = {1, 4} and Y = {3, 4, 5}. 3. Find the complement of set P given the universal set U = {1, 2, 3, 4, 5, 6} and P = {2, 5}. 4. Find the set difference of sets C and D given that C = {10, 20, 30} and D = {1, 10} 5. Find the power set of the set A = {1, 4} 6. What are the number of elements in the union of two sets P and Q with number of elements 10, 8 respectively. Also the number of common elements in both sets is 3. 7. Find the number of elements in the intersection of two sets given the number of elements of sets U and V are 5 and 7 and the number of elements in their union is 10. Practice Questions on Operations on Sets – FAQsWhat is difference of set?
What are the 4 Types of Set Operations?
What does ∩ and ∪ Mean in Math?
What are the Properties of Sets and Operations?
|
Reffered: https://www.geeksforgeeks.org
| Mathematics |
| Related |
|---|
| |
| |
| |
| |
| |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 13 |