Inequalities that involve algebraic expressions with absolute value symbols and inequality symbols are called Absolute Value Inequality. In this article, we will discuss inequalities and absolute value inequalities and others in detail.

What is Inequalities?

Inequalities can be understood as the complement of equations. Inequalities are used to establish a relationship between two or more mathematical values based on the unequal relationship between them. Let us look at an example

• 5 + x > y + 10
• x > y + 5

The above relationship indicates that x is not equal to y+5 rather it is greater than the value of y after 5 is added to it.

What is Absolute Value Inequalities?

Absolute Value Inequalities are a subcategory of inequalities that compare absolute values of mathematical quantities. These usually include symbols like >, < which denote unequal relationships.

What is Absolute Value?

Let us see the formal definition

An absolute value inequality is an expression that uses absolute value expression and variables to denote the relationship between quantities.

We can categorize the inequality into two major types:

• Lesser Than or Equal To
• Greater Than or Equal To
• Compound Inequalities with Absolute Values

Each of the given types is denoted using different symbols which will be discussed later.

Example of Absolute Value Inequalities

Here are some examples to understand the Absolute Value Inequalities

• |x + 5| < 8
• -13 < x < 3

Solving Absolute Value Inequalities

We use number line approach to solve an inequality and follow the steps added below:

Step 1: Write down the inequality and assume it to be an equality making it an equation instead of inequation.

Step 2: Draw a number line depending on the intervals and represent the equation on the number line.

Step 3: From each interval, select a number and check if it satisfies the inequality.

Step 4: Perform step 3 for every interval and the intervals for which a random number satisfies the inequality will be included in your final answer.

Step 5: Take the union of all the intervals to get the answer.

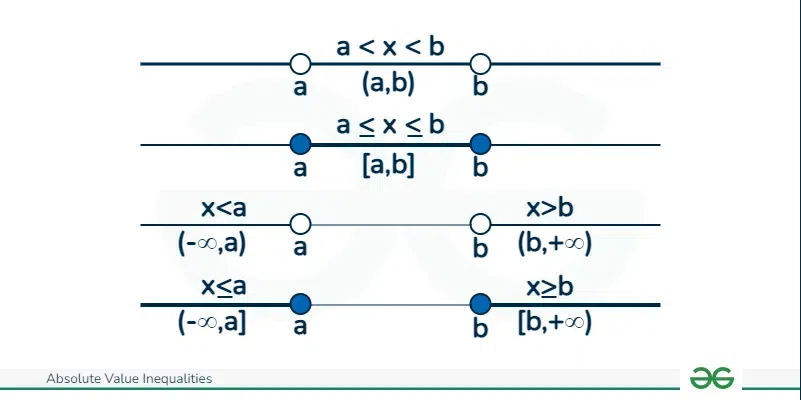
Graphical Representation of Inequalities

We can use a graph to plot the inequalities and find the corresponding solution for the inequalities. Let us see how we can use the graph to plot the solution

Note: Open dot ◌ is used for representing an open interval whereas a closed dot ⚈ is used to represent a closed interval in the graph.

Here is the representation of different cases:

Representation of Inequalities

Types of Absolute Value Inequalities

Depending on the type of sign in the inequality, there are different types of inequalities which are mentioned below:

• Inequalities with Greater Than Condition
• Inequalities with Less Than Condition
• Compound Inequalities Involving Absolute Values

Inequalities with Greater Than Condition

These inequalities generally use a greater than sign i.e. the number is greater than the value of some other mathematical value. Here are some examples of such inequalities

• x > 5
• x+ y > 7 + 3y
• 65y > x + 22

Inequalities with Less Than Condition

These inequalities generally use a less-than sign i.e. the number is less than the value of some other mathematical value. Here are some examples of such inequalities

• x < 57
• x + y < 89
• 5y + 6x < 0

Compound Inequalities Involving Absolute Values

As the name suggests, Compound Inequalities involve both greater than and less than cases i.e. the number is less than and greater than the value of some other mathematical value. These inequalities use the absolute value. Here are some examples of such inequalities

• |x – 5| < 7
• |x + 6y| > 89
• |4x + 2| <= 24

Intersection and Union in Absolute Value Inequalities

Let us understand how we can take Intersection and Union in Absolute Value Inequalities.

Union of Inequalities

For a given set of values, if the inequality is x>=a or x<b then we need to find the union of the values of x which can be given by

Case 1: x >= a or x < b

{x: x < b U x ≥ a}

Case 2: x < a or x >= b

{x: x <a U x ≥ b} = {x: x < a}∪{x: x ≥ b}.

The solution i.e. the union can be calculated using graph. Consider the example x <= 3 || x >= -4 , then the union of the inequalities will give an overlapping interval which will include all real numbers as shown below.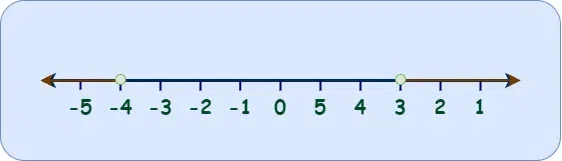

Union of Inequalities

Intersection of Inequalities

For a given set of values, if the inequality is x >= a and x < b then we need to find the intersection of the values of x which can be given by

Case 1: a <= x < b

{x: a≤x < b}

Case 2: a <= x U b > x

{x: a ≤ x U x < b}

The solution i.e. the intersection can be calculated using graph. Consider the example x <= 4 U x >= -5 , then the intersection of the inequalities will give an interval which will include all real numbers from -5 and 4 as shown below.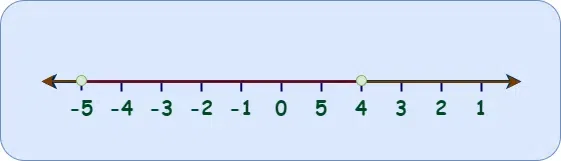

Intersection of Inequalities

Read More:

• Triangle Inequality
• Compound Inequalities
• Word Problems of Linear Inequalities

Examples on Absolute Value Inequalities

Example 1: Solve for inequality |x+24|>-5 using the formula-based approach.

Solution:

Given Inequality

|x + a| > b

• -∞ < x + a < -b
• b < x + a < +∞

Solving both of them individually

Case 1:

-∞ < x < -a – b

Case 2:

b – a < x < ∞

x ⋿ (-∞,-a-b) ⋃ (b-a, ∞)

Example 2: Solve this less than equal to absolute inequality |y + 5| <= 3y

Solution:

Given Inequality

• |y + 5| <= 3y

Case 1:

y + 5 <= 3y

5 <= 2y

5/2 <= y

y ϵ [5/2, ∞)…(i)

Case 2:

-3y <= y + 5

-4y <= 5

y >= -1.25

y ϵ (-∞, -5/4]…(ii)

From eq. (i) and eq. (ii)

y ϵ [5/2, -5/4]

Practice Problems on Absolute Value Inequalities

P1. Use the union and intersection method to find the solution for x given |x+7|<1001 and |x+2|>24.

P2. Use the graphical representation method to find the solution of |2x+5|+y>7x

P3. Solve the inequality ∣2x + 3∣ < 5.

P4. Find all values of such that ∣x − 4∣ ≥ 2.

FAQs Absolute Value Inequalities

When do we use curved and square brackets while writing the solution of inequality?

Curved bracket i.e. ( ) is used to denote a quantity that is not included in the range of possible values of the variable whereas the square bracket i.e. [ ] is used when the number is included in the range of values of the variable.

What are the equivalents of curved and square brackets in graphical representation?

• Open dot denotes the curved bracket.
• Closed dot is used instead of the square bracket.

When is the sign switched from negative to positive and vice-versa in an inequality?

Sign in an inequality changes when we multiply the quantity on both sides of the equation by a negative sign or divide the quantity on both sides by a negative value.

Can an absolute value inequality be negative?

No, absolute value inequality can never be negative.