
|
|
Eccentricity of Ellipse: eccentricity is a measure that describes how much a conic section deviates from being circular. For any point on a conic section, eccentricity is defined as the ratio of the distance to a fixed point (focus) to the distance to a fixed line (directrix). The eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse. It is denoted using the letter, ‘e’ and is calculated as, e = c/a where a is the length of the semi-major axis and c is the distance from the centre to the foci. In this article, we will learn about Ellipse, Eccentricity of Ellipse, Formula for eccentricity of ellipse and others in detail. 
Table of Content What is an Ellipse?An ellipse in mathematics is a special shape that we get when we cut through a cone at an angle. It looks like a stretched-out circle or an elongated oval. Imagine slicing through a cone sideways with a knife, not straight across but at a slant. The shape you get where the knife cuts through the cone is an ellipse. Eccentricity of EllipseAn ellipse is a shape formed by a point moving in a way that its distance from a fixed point and a fixed line always have a certain relationship. This is such that the ratio of the distance from the point to the distance from the line remains constant, and this constant ratio is always less than one. The constant ratio is denoted by ‘e’ and is known as the eccentricity of the ellipse. The eccentricity of an ellipse is a measure of how stretched or elongated the ellipse is. It is a dimensionless parameter that ranges from 0 to 1. Suppose the distance of the focus from the centre of the ellipse is ‘c’ and the distance of the end of the ellipse from the centre is ‘a’, then eccentricity of the ellipse is found by the formula: e = c/a Eccentricity of Ellipse FormulaEccentricity of an ellipse is defined as the ratio of the distance between the foci to the length of the major axis i.e the formula for eccentricity is given by:
Where,
For any ellipse, let a be the length of its semi-major axis and b be the length of its semi-minor axis. In the coordinate system with the origin at the centre of ellipse and x-axis with the major axis, equation of ellipse is, (x/a)2 + (y/b)2 = 1 with foci at coordinates (±c, 0) for c = √ (a2 – b2) Formula of eccentricity of ellipse is:
Eccentricity of Ellipse- DiagramDiagram of Ellipse is shown in the image added below: 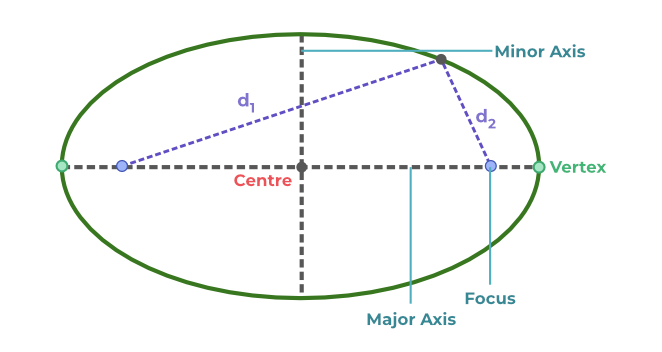 Diagram of Ellipse Various results related to ellipse:
Eccentricity of CircleA circle is a set of points in a plane that are all the same distance from a fixed point known as the “centre”. The distance from the centre to any point on the circle is called the “radius”. If the distance from the centre to focus is zero or in other way the centre of the circle is at the origin of a cartesian plane, we derive the equation of a circle. This Eccentricity presents a uniform circular shape. Elements of Circle
Eccentricity of ParabolaA parabola is defined as a set of points in a plane equidistant from a fixed line called the directrix and a fixed point called the focus. Put simply, the distance from the focus in the plane always has a constant ratio with the distance from the directrix in the plane. Elements of Parabola
Eccentricity of EllipseAn ellipse is a closed curve that is symmetric with respect to two perpendicular axes. It can also be defined as the set of all points in a plane, such that the sum of the distances from any point on the curve to two fixed points (called foci) is constant. Elements of Ellipse
Eccentricity of HyperbolaA hyperbola is a conic section that is formed when a plane intersects a double right circular cone at an angle. The intersection produces two separate unbounded curves that are mirror images of each other. A hyperbola is an open curve with two branches. The plane does not have to be parallel to the axis of the cone; the hyperbola will be symmetrical in any case. Elements of Hyperbola
Key properties of circles, parabolas, ellipses, and hyperbolas:
Derivation of Eccentricity of EllipseRatio of the distance between the foci of the ellipse to the length of the major axis is called eccentricity of ellipse. Let’s consider an ellipse with a semi-major axis of length a and a semi-minor axis length b. The foci of the ellipse are located at a distance c from the center where c can be calculated using the relationship: c = √(a2-b2)…(i) And eccentricity is given by: e = c/a…(ii) Placing the value of c from (i) in (ii): e = √(a2-b2) /a…(iii) Squaring on both sides of (iii) e2 = {√(a2-b2) /a}2 e2 = (a2 – b2)/a2 Rearranging the above equation: a2e2 = a2 – b2 a2e2+b2 = a2 (a2e2 + b2)/a2 = 1 a2e2/a2 + b2/a2 = 1 e2 + b2/a2 = 1 e2 = 1 – b2/a2
e = √{ 1 – ( 2b/2a )2}
Hence we have derived the equation (iv), known as the eccentricity formula for an ellipse. People Also Read:Eccentricity of Ellipse ExamplesExample 1: For the following ellipse find the eccentricity of the ellipse:
Solution:
Example 2: If the latus rectum of an ellipse is equal to half of the minor axis, find its eccentricity. Solution:
Example 3: If the eccentricity of an ellipse is 5/8 and the distance between its foci is 10 , then find the latusrectum of the ellipse. Solution:
Example 4: Find the distance between the directrices the ellipse x2/36 + y2/20 = 1 Solution:
Example 5: Find the equation of the ellipse whose axes are along the coordinate axes ,vertices are (±5,0) and foci at (±4,0) . Solution:
Practice Problems on Eccentricity of Ellipse1. Given an ellipse with a semi-major axis a = 5 units and a semi-minor axis b = 3 units, calculate the eccentricity of the ellipse. 2. An ellipse has an eccentricity of 0.8 and a semi-major axis of 10 units. Find the length of the semi-minor axis b 3. The distance between the foci of an ellipse is 8 units, and the length of the major axis is 10 units. Determine the eccentricity of the ellipse. 4. An ellipse has an eccentricity that is 1/2 of its semi-major axis length. If the semi-minor axis is 6 units, find the eccentricity and the length of the semi-major axis. Eccentricity of Ellipse – FAQsWhat is eccentricity?
What is Eccentricity of Ellipse?
What does an eccentricity 0 mean for an ellipse?
Can the eccentricity of an ellipse be greater than 1?
How does changing the eccentricity affect the focus of an ellipse?
Is Eccentricity of Ellipse greater or less than 1?
What is an eccentricity formula?
What is eccentricity of ellipse formula in terms of a and b?
|
Reffered: https://www.geeksforgeeks.org
| Mathematics |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 15 |