One to One Function or One-One Function is one of the types of functions defined over domain and codomain and describes the specific type of relationship between domain and the codomain. One to One Function is also called the Injective Function. One to One Function is a mathematical function where each element in the domain maps to a unique element in the codomain.

This article explores the concept of One to One Function or One-One Function in detail including its definition and examples which help you understand the concept with ease. We will also discuss some sample problems and provide some practice problems for you to solve. So, let’s learn about this important concept in mathematics known as One to One Function.

What is One-to-One Function?

A one-to-one function, also known as an injective function, is one where different elements of A have different elements related to B or different elements of A have different images in B.

If there are different images for a function that means it is only possible for one-to-one if the pre-images were different if B set has different elements that means it is only possible when A set had different elements for which these were the pre-images.

One to One Function Definition

A function ‘f’ from a set ‘A’ to set ‘B’ is one-to-one if no two elements in ‘A’ are mapped to same element in ‘B.’

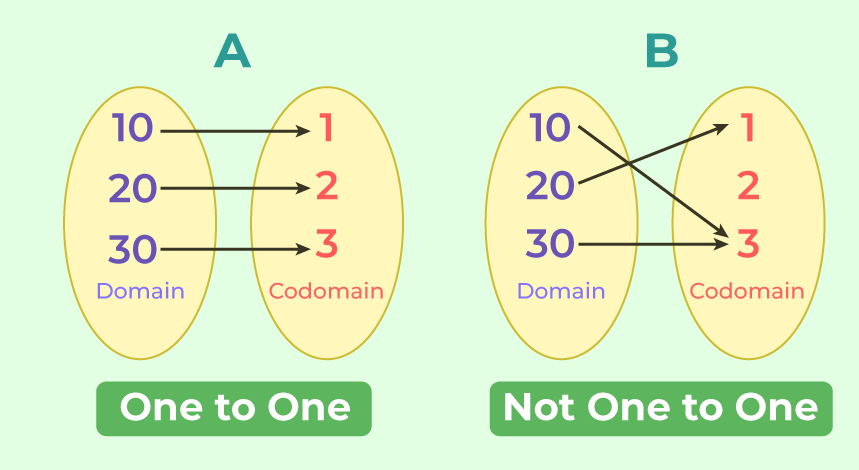
Let’s consider these two diagrams. For diagram A we realize that 10 maps to 1, 20 maps to 2 and 30 maps to 3.

However for diagram B it is clear that 10 and 30 maps to 3 and then 20 maps to 1.

Since we have elements in the domain corresponding to distinct values in the each domain for diagram A it makes the function one-to-one, thus our diagram B is not one to one.

This can be expressed mathematically as

f(a) = f(b) ⇒ a = b

Example of One-to-One Functions

• Identity Function: The identity function is a simple example of a one-to-one function. It takes an input and returns the same value as the output. For any real number x, the identity function is defined as:

f(x) = x

Every distinct input x corresponds to a distinct output f(x), making it a one-to-one function.

• Linear Function: A linear function is one where the highest power of the variable is 1. For example:

f(x) = 2x + 3

This is a one-to-one function because no matter what value of x you choose, you will get a unique value for f(x).

• Absolute Value Function: The absolute value function f(x)=∣x∣ is also a one-to-one function. For any real number x, the absolute value function returns a non-negative value, and different values of x will result in different absolute values.

Let’s prove one such examples for one-to-one function.

Example: Prove that the function f(x) = 1/(x+2), x≠2 is one-to-one.

Solution:

According one-to-one function we know that

f(a) = f(b)

replace a with x and x with b

f(a) = 1/(a+2) , f(b) = 1/(b+2)

⇒ 1/(a+2) = 1/(b+2)

cross multiply the above equation

1(b+2)=1(a+2)

b+2=a+2

⇒ b=a+2-2

∴ a=b

Now, since a = b the function is said to be one-to-one function.

Properties One-to-One Functions

Let’s consider f and g are two one-to-one function, the properties are as follows:

• If f and g are both one to one, then f ∘ g follows injectivity.
• If g ∘ f is one to one, then function f is one to one, but function g may not be.
• f: X → Y is one-one, if and only if, given any functions g, h : P → X whenever f ∘ g = f ∘ h, then g = h. In other words, one-one functions are exactly the monomorphisms in the category set of sets.
• If f: X → Y is one-one and P is a subset of X, then f^-1(f(A)) = P. Thus, P can be retrieved from its image f(P).
• If f: X → Y is one-one and P and Q are both subsets of X, then f(P ∩ Q) = f(P) ∩ f(Q).
• If both X and Y are limited with the same number of elements, then f: X → Y is one-one, if and only if f is surjective or onto function.

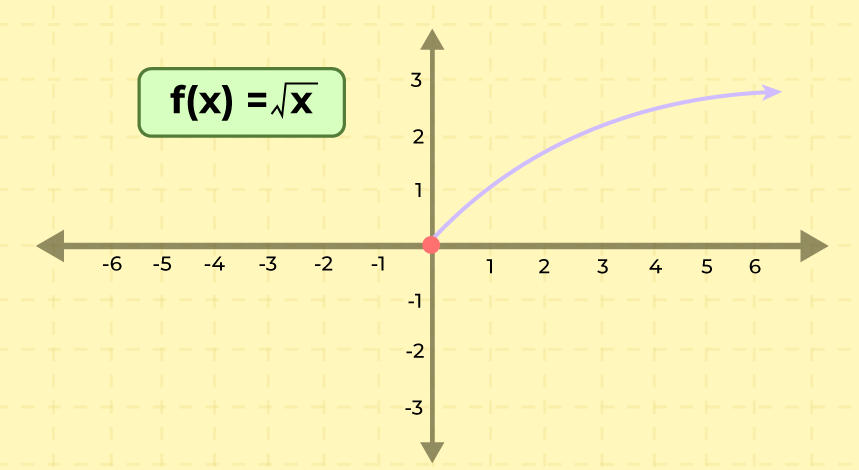
Graph of one-to-one function

Let’s see one of the graph representation of one-to-one function

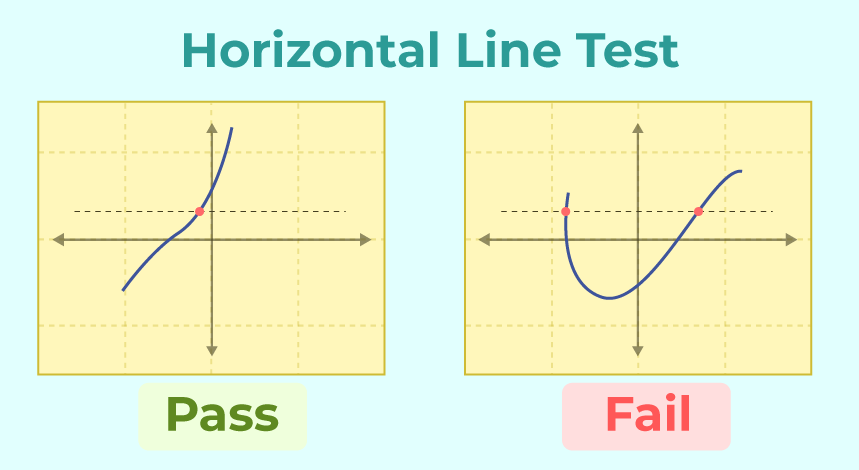
The above graph of function f(x)= √x show the graphical representation of one-to-one function.

Horizontal Line Test

A function is one-to-one if each horizontal line does not intersect the graph at more that one point.

Let’s use a linear function as example. Let’s call it f(x) , so f(x) have an inverse function. To determine if f(x) have an inverse function you have to show that it’s a one-to-one function, you have to show that it passes the horizontal line test. So if we draw a horizontal line and if f(x) touches horizontal line more than once that means f(x) is not a one-to-one function and it does not have an inverse function.

In the above example it only intersect the horizontal line only at one point. So f(x) is one-to-one function which means that it has an inverse function.

Inverse of one-to-one function

Let f be a one-to-one function with a domain A and Range B. Then the inverse of f is a function with domain B and Range A defined by f^-1 (y) =x if and only if f(x)=y for any y in B. Always remember a function has an inverse if and only if it is one-to-one. A function is one-to-one if the highest exponent is an odd number. But if the highest number is an even number or an absolute value this is not one-to-one function.

Example: f(x)=3x+2 find the inverse of the function

Solution:

write the function in y=f(x) form

⇒ y=3x+2

lets interchange y and x variables

⇒ x=3y+2

solve y in terms of x

⇒ x-2=3y

divide the equation with 3

⇒ (x-2)/3=3y/3

⇒ y=(x-2)/3

∴ f-1(x)=(x-2)/3

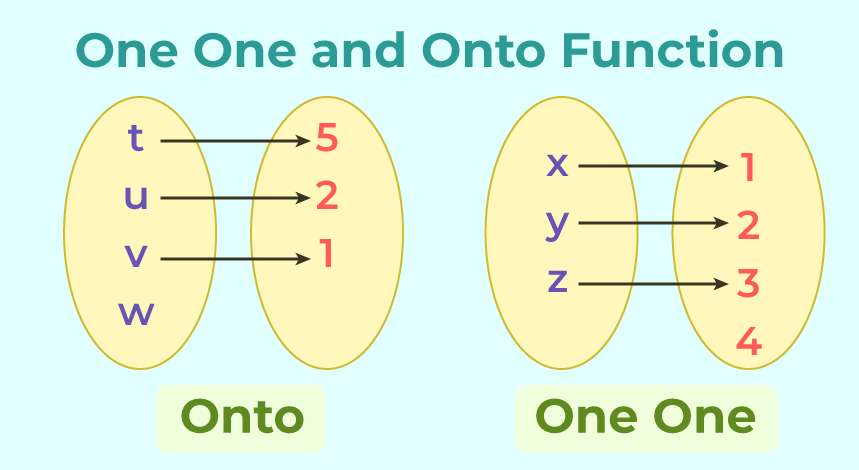
One to One Function and Onto Function

The key differences between One to One and Onto Functions are listed in the following table:

The following illustration provide the clear difference between one one and onto function:

Read More,

• Functions
• Types of Functions
• Relation and Function

Solved Problems on One to One Function

Let’s solve some problems to illustrate one-to-one functions:

Problem 1: Determine if the following function is one-to-one: f(x) = 3x – 1

Solution:

Solution 1: To check if it’s one-to-one, we need to show that no two distinct x-values map to the same y-value.

Suppose f(a) = f(b), where a ≠ b.

3a – 1 = 3b – 1

3a = 3b

a = b

Since the only way for f(a) = f(b) is when a = b, this function is indeed one-to-one.

Problem 2: Determine if the following function is one-to-one: g(x) = x²

Solution:

Solution 2: We’ll use the horizontal line test by graphing the function. If any horizontal line intersects the graph more than once, it’s not one-to-one.

The graph of g(x) = x^2 is a parabola opening upwards. Any horizontal line only intersects the graph once, so this function is not one-to-one.

Practice Problems on One to One Functions

Problem 1: Determine whether the following function is one-to-one:

• f(x) = 2x + 3
• g(x) = 3x² – 1
• h(x) = ³√x

Problem 2: Find a function that is one-to-one from the set of real numbers to the set of real numbers.

Problem 3: Given the function g(x) = x² + 1, determine if it is one-to-one on its entire domain.

Problem 4: Consider the function h(x) = e^x. Is it a one-to-one function?

Problem 5: Find the inverse function of f(x) = 4x – 7 and determine its domain.

Problem 6: Determine if the function p(x) = √x is one-to-one.

Problem 7: Given q(x) = x/2, find the domain and range of the function.

Problem 8: Check whether the function r(x) = sin (x) is one-to-one over the interval [0, π].

Problem 9: Consider the function s(x) = |x|. Is it a one-to-one function?

Problem 10: Determine if the function t(x) = 1/x is one-to-one and find its domain.

One to One Functions – FAQs

1. What is a one-to-one function?

A one-to-one function is a mathematical function that maps each element in its domain to a unique element in its codomain. In other words, it doesn’t map two different elements in the domain to the same element in the codomain.

2. How can I determine if a function is one-to-one?

You can use the horizontal line test. If no horizontal line intersects the graph of the function more than once, it is a one-to-one function.

3. What is the difference between a one-to-one function and an onto function?

A one-to-one function ensures that no two distinct elements in the domain map to the same element in the codomain, while an onto function, also known as a surjective function, ensures that every element in the codomain is mapped to by at least one element in the domain.

4. Are all linear functions one-to-one?

No, not all linear functions are one-to-one. For example, f(x) = 2x is one-to-one, but g(x) = 2x + 1 is not because it maps two different x-values to the same y-value (e.g., g(1) = 3 and g(2) = 5).