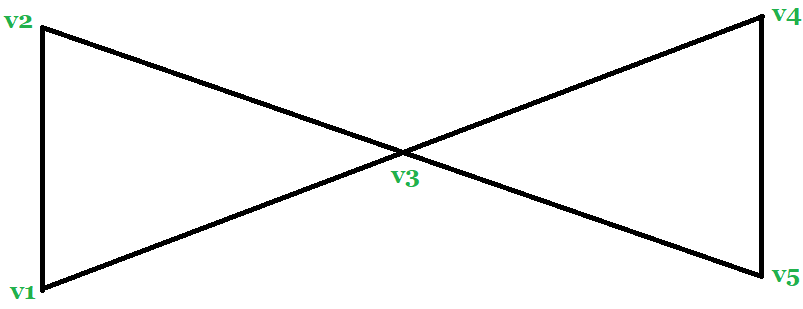
Prerequisites: Walks, trails, paths, cycles, and circuits in a graph

If some closed walk in a graph contains all the vertices and edges of the graph, then the walk is called an Euler Line or Eulerian Trail and the graph is an Euler Graph. In this article, we will study the Euler graph and arbitrarily traceable graph. 

Consider an Euler Graph shown in the figure. Let us start from vertex v1 and trace the path v1 v2 v3. Here at v3, we have an option of going to v1, v3, or v4. If we go for the first option then we would trace the circuit v1 v2 v3 v1, which is not an Euler line. From here we can conclude that starting from vertex v1, it is not always that the entire Euler line can be traced by moving along any edge that has not been traced earlier.

 

Now the following question arises: Is there any property that a vertex has in an Euler graph such that an Euler line is always obtained when one follows any walk according to a particular rule that whenever one reaches a vertex one should select any edge, which is not previously traversed?

A graph of this type is called an arbitrarily traceable graph from vertex v. The graph shown in the above figure is an arbitrarily traceable graph from vertex v3 but not from any vertex. The graph shown in the figure is not an arbitrarily traceable graph from any vertex.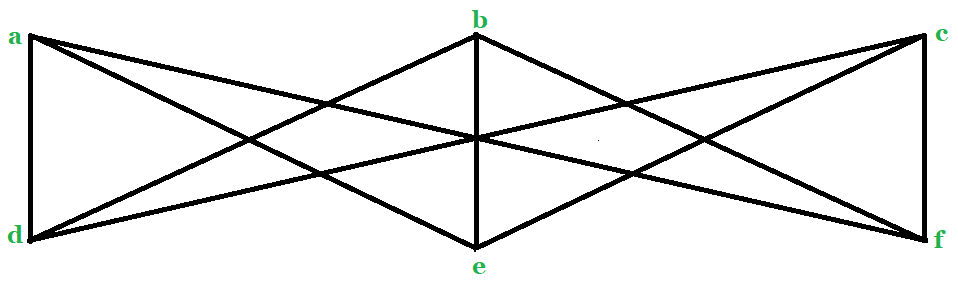 

 

 

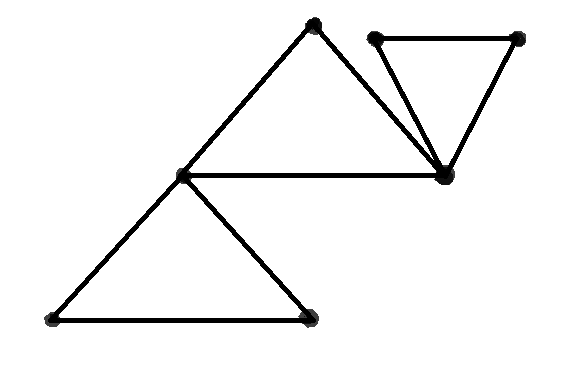
So, if we want to know whether a graph is arbitrarily traceable or not, we can use the following theorem “An Euler Graph G is arbitrarily traceable from vertex v in G if every circuit in G contains v”.