Horje
Delete Maximum edges such that Graph is traversable

Given an undirected graph of N node, where nodes are numbered from 1 to N, and an array of edges, where edges[i] = {edgeType, u, v} and two persons A and B are moving in it. Each edge type indicates different things. 

  • edgeType = 0 indicates that only A can travel on that edge from node u to v.
  • edgeType = 1  indicates that only B can travel on that edge from node u to v. 
  • edgeType = 2, then both persons can travel on that edge. 

The task is to delete the maximum number of edges such that both persons still travel on all the nodes starting from any node or return -1 if both persons cannot fully traverse the graph.

Examples:

Input: N = 4, edges =  { { 0, 1, 2 }, {0, 3, 4}, {1, 1, 2}, {1, 2, 4}, { 2, 1, 2 }, { 2, 1, 3 } }
Output: 2
Explanation: Remove an edge between node 1 and node 2 which have edgeType = 0
Remove an edge between node 1 and node 2 which have edgeType = 1
The final node remaining is traversable by both the person.
 

The above graph

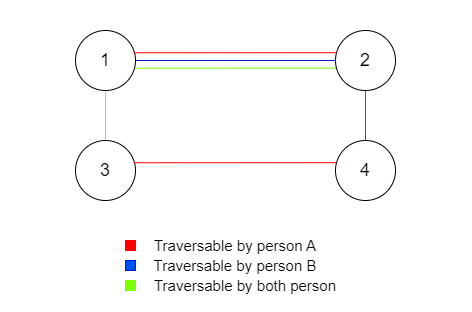The above graph

Input: N = 2, edges = { { 0, 1, 2 }, { 1, 1, 2 }, { 2, 1, 2 } }
Output: 2

An approach using Greedy + Disjoint union set (DSU):

Sort the edges[] on the basis of edgeType which is traversable by both. Use DSU for keeping track of number of connected component for both the person individually and initially assign count of connected component to N as we’ll assume every node an individual component. 

  • Try to connect edges which are traversable in their DSU, if edges are not redundant then add that edge and reduce the number of connected component by 1 for that person. Otherwise, remove that edge. 
  • Finally check if any one have number of connected component greater than 1, means that person can’t traverse every node. So, return -1. Otherwise, return count of remove.

Follow the steps below to implement the above idea:

  • Sort on the basis of that edge which is traversable by both person
  • Initialize a parentA[] for person A, parentB[] for person B
  • Initialize a rankA[] for person A, rankB[] for person B
  • Initially, every node is its own parent and make its rank = 1.
  • Create variable connectedComponentA and connectedComponentB to count the number of connected components where A and B can travel respectively.
  • Create a remove variable to keep track of how many redundant nodes can be removed.
  • Iterate over all the edges:
    • Connect that node with edges first which is traversable by both, (i.e, edgeType = 2)
      • Try to merge node into DSU for person A.
      • Try to merge node into DSU for person B.
      • If there is a merge of nodes in DSU for person A.
        • Decrement connectedComponentA by 1.
      • If there is a merge of nodes in DSU for person B.
        • Decrement connectedComponentB by 1.
      • If there is no merge of nodes in both the DSU
        • This edge is redundant. So, increment remove.
    • For edges with edgeType=0, try to merge node into DSU for person A
      • If there is a merge of nodes in DSU for person A.
        • Decrement connectedComponentA by 1.
      • If there is no merge of nodes in person A’s DSU.
        • This edge is redundant. So, increment remove.     
    • For edges with edgeType = 1, try to merge node into DSU for person B
      • If there is a merge of nodes in DSU for person B.
        • Decrement of connectedComponentB  by 1
      • If there is no merge of nodes in person B’s DSU
        • This edge is redundant. So, increment remove.
  • Finally, check if anyone’s connected Component is not 1:
    • Then, there is no way to travel on all the nodes by both people. So, return -1 
    • Otherwise, return the remove count.

Below is the implementation of the above approach.

C++

// C++ code to implement the approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to be used as comparator for sorting
bool static cmp(vector<int>& a, vector<int>& b)
{
    return a[0] > b[0];
}
 
// Function to find the parent of a node
int find(int x, vector<int>& parent)
{
    if (parent[x] == x)
        return x;
 
    return parent[x] = find(parent[x], parent);
}
 
// Function to create union of two disjoint sets
bool union1(int x, int y, vector<int>& parent,
            vector<int>& rank)
{
    int lx = find(x, parent);
    int ly = find(y, parent);
 
    // Merge their leader
    if (lx != ly) {
        if (rank[lx] > rank[ly]) {
            parent[ly] = lx;
        }
        else if (rank[lx] < rank[ly]) {
            parent[lx] = ly;
        }
        else {
            parent[lx] = ly;
            rank[ly] += 1;
        }
 
        return true;
    }
    return false;
}
 
// Function to find the maximum number
// of edges that can be deleted
int removeMaxEdges(int n, vector<vector<int> >& edges)
{
    int n1 = n + 1;
 
    // Sort on the basis on that edge
    // which is traversable by both person
    sort(edges.begin(), edges.end(), cmp);
 
    // Initialize a parentA[] for person A,
    // parentB[] for person B Initialize a
    // rankA[] for person A, rankB[]
    // for person B
    vector<int> parentA(n1), parentB(n1), rankA(n1),
        rankB(n1);
 
    // Initially every node as leader and
    // make their rank = 1.
    for (int i = 1; i <= n; i++) {
        parentA[i] = i;
        parentB[i] = i;
        rankA[i] = 1;
        rankB[i] = 1;
    }
 
    // Create variable connectedComponentA
    // to count number of connected
    // component where A can travel Create
    // variable connectedComponentB to
    // count number of connected component
    // where B can travel Create a remove
    // variable to keep track of how many
    // redundant node that need to remove.
    int connectedComponentA = n, connectedComponentB = n,
        remove = 0;
 
    // Iterate over all the edges.
    for (auto i : edges) {
 
        // Connect the node with edges
        // first which is traversable
        // by both
        if (i[0] == 2) {
 
            // Try to merge node into DSU
            // for person A
            bool mergeA
                = union1(i[1], i[2], parentA, rankA);
 
            // Try to merge node into DSU
            // for person B
            bool mergeB
                = union1(i[1], i[2], parentB, rankB);
 
            // If there is merge of nodes
            // in DSU for person A. then,
            // decrement of
            // connectedComponentA by 1
            if (mergeA) {
                connectedComponentA--;
            }
 
            // If there is merge of nodes
            // in DSU for person B. then,
            // decrement of
            // connectedComponentB by 1
            if (mergeB) {
                connectedComponentB--;
            }
 
            // If there is no merge of
            // nodes in both the DSU's then,
            // this edge is redundant. So,
            // increment remove.
            if (mergeA == false && mergeB == false) {
                remove++;
            }
        }
 
        else if (i[0] == 1) {
 
            // Try to merge node into DSU
            // for person A
            bool mergeA
                = union1(i[1], i[2], parentA, rankA);
 
            // If there is merge of nodes
            // in DSU for person A.
            // then, decrement of
            // connectedComponentA by 1
            if (mergeA) {
                connectedComponentA--;
            }
 
            // If there is no merge of
            // nodes in person A's DSU then,
            // this edge is redundant. So,
            // increment remove.
            if (mergeA == false) {
                remove++;
            }
        }
 
        else {
 
            // Try to merge node into DSU
            // for person B
            bool mergeB
                = union1(i[1], i[2], parentB, rankB);
 
            // If there is merge of nodes
            // in DSU for person B. then,
            // decrement of
            // connectedComponentB  by 1
            if (mergeB) {
                connectedComponentB--;
            }
 
            // If there is no merge of
            // nodes in person B's DSU
            // then, this edge is redundant.
            // So, increment remove.
            if (mergeB == false) {
                remove++;
            }
        }
    }
 
    // Finally check if if any one's
    // connected Component is not 1,
    // then, there is no way to travel on
    // all the node by both person.
    // So, return -1
    if (connectedComponentA != 1
        || connectedComponentB != 1) {
        return -1;
    }
 
    // Otherwise, return remove count.
    return remove;
}
 
// Driver code
int main()
{
    int N = 4;
    vector<vector<int> > edges
        = { { 0, 1, 2 }, { 0, 3, 4 }, { 1, 1, 2 }, { 1, 2, 4 }, { 2, 1, 2 }, { 2, 1, 3 } };
 
    // Function Call
    cout << removeMaxEdges(N, edges);
 
    return 0;
}

Java

/*package whatever //do not write package name here */
// java code addition
import java.io.*;
import java.util.*;
 
class GFG {
 
  // Function to find the parent of a node
  public static int find(int x, List<Integer> parent)
  {
    if (parent.get(x) == x)
      return x;
    parent.set(x, find(parent.get(x), parent));
    return parent.get(x);
  }
 
  // Function to create union of two disjoint sets
  public static boolean union1(int x, int y,
                               List<Integer> parent,
                               List<Integer> rank)
  {
    int lx = find(x, parent);
    int ly = find(y, parent);
 
    // Merge their leader
    if (lx != ly) {
      if (rank.get(lx) > rank.get(ly)) {
        parent.set(ly, lx);
      }
      else if (rank.get(lx) < rank.get(ly)) {
        parent.set(lx, ly);
      }
      else {
        parent.set(lx, ly);
        rank.set(ly, rank.get(ly) + 1);
      }
 
      return true;
    }
    return false;
  }
 
  // Function to find the maximum number
  // of edges that can be deleted
  public static int
    removeMaxEdges(int n, List<List<Integer> > edges)
  {
    int n1 = n + 1;
 
    // Sort on the basis on that edge
    // which is traversable by both person
 
    Collections.sort(
      edges, new Comparator<List<Integer> >() {
        @Override
        public int compare(final List<Integer> a,
                           List<Integer> b)
        {
          if (a.get(0) > b.get(0))
            return -1;
          return 1;
        }
      });
    // Initialize a parentA[] for person A,
    // parentB[] for person B Initialize a
    // rankA[] for person A, rankB[]
    // for person B
    List<Integer> parentA = new ArrayList<Integer>();
    List<Integer> parentB = new ArrayList<Integer>();
    List<Integer> rankA = new ArrayList<Integer>();
    List<Integer> rankB = new ArrayList<Integer>();
 
    for (int i = 1; i <= n1; i++) {
      parentA.add(0);
      parentB.add(0);
      rankA.add(0);
      rankB.add(0);
    }
 
    // Initially every node as leader and
    // make their rank = 1.
    for (int i = 1; i <= n; i++) {
      parentA.set(i, i);
      parentB.set(i, i);
      rankA.set(i, 1);
      rankB.set(i, 1);
    }
 
    // Create variable connectedComponentA
    // to count number of connected
    // component where A can travel Create
    // variable connectedComponentB to
    // count number of connected component
    // where B can travel Create a remove
    // variable to keep track of how many
    // redundant node that need to remove.
    int connectedComponentA = n,
    connectedComponentB = n, remove = 0;
 
    // Iterate over all the edges.
    for (int j = 0; j < edges.size(); j++) {
      List<Integer> i = edges.get(j);
      // Connect the node with edges
      // first which is traversable
      // by both
      if (i.get(0) == 2) {
 
        // Try to merge node into DSU
        // for person A
        boolean mergeA = union1(i.get(1), i.get(2),
                                parentA, rankA);
 
        // Try to merge node into DSU
        // for person B
        boolean mergeB = union1(i.get(1), i.get(2),
                                parentB, rankB);
 
        // If there is merge of nodes
        // in DSU for person A. then,
        // decrement of
        // connectedComponentA by 1
        if (mergeA) {
          connectedComponentA--;
        }
 
        // If there is merge of nodes
        // in DSU for person B. then,
        // decrement of
        // connectedComponentB by 1
        if (mergeB) {
          connectedComponentB--;
        }
 
        // If there is no merge of
        // nodes in both the DSU's then,
        // this edge is redundant. So,
        // increment remove.
        if (mergeA == false && mergeB == false) {
          remove++;
        }
      }
 
      else if (i.get(0) == 1) {
 
        // Try to merge node into DSU
        // for person A
        boolean mergeA = union1(i.get(1), i.get(2),
                                parentA, rankA);
 
        // If there is merge of nodes
        // in DSU for person A.
        // then, decrement of
        // connectedComponentA by 1
        if (mergeA) {
          connectedComponentA--;
        }
 
        // If there is no merge of
        // nodes in person A's DSU then,
        // this edge is redundant. So,
        // increment remove.
        if (mergeA == false) {
          remove++;
        }
      }
 
      else {
 
        // Try to merge node into DSU
        // for person B
        boolean mergeB = union1(i.get(1), i.get(2),
                                parentB, rankB);
 
        // If there is merge of nodes
        // in DSU for person B. then,
        // decrement of
        // connectedComponentB  by 1
        if (mergeB) {
          connectedComponentB--;
        }
 
        // If there is no merge of
        // nodes in person B's DSU
        // then, this edge is redundant.
        // So, increment remove.
        if (mergeB == false) {
          remove++;
        }
      }
    }
 
    // Finally check if if any one's
    // connected Component is not 1,
    // then, there is no way to travel on
    // all the node by both person.
    // So, return -1
    if (connectedComponentA != 1
        || connectedComponentB != 1) {
      return -1;
    }
 
    // Otherwise, return remove count.
    return remove;
  }
 
  public static void main(String[] args)
  {
    int N = 4;
    List<List<Integer> > edges
      = new ArrayList<List<Integer> >();
 
    List<Integer> a = new ArrayList<Integer>();
    a.add(0);
    a.add(1);
    a.add(2);
    edges.add(a);
    List<Integer> b = new ArrayList<Integer>();
    b.add(0);
    b.add(3);
    b.add(4);
    edges.add(b);
    List<Integer> c = new ArrayList<Integer>();
    c.add(1);
    c.add(1);
    c.add(2);
    edges.add(c);
    List<Integer> d = new ArrayList<Integer>();
    d.add(1);
    d.add(2);
    d.add(4);
    edges.add(d);
    List<Integer> e = new ArrayList<Integer>();
    e.add(2);
    e.add(1);
    e.add(2);
    edges.add(e);
    List<Integer> f = new ArrayList<Integer>();
    f.add(2);
    f.add(1);
    f.add(3);
    edges.add(f);
 
    // Function Call
    System.out.println(removeMaxEdges(N, edges));
  }
}
 
// This code is contributed by ksam24000.

C#

// C# implementation
 
using System;
using System.Collections;
using System.Collections.Generic;
 
public class GFG {
 
  // Function to be used as comparator for sorting
  public static int cmp(List<int> a, List<int> b)
  {
    if (a[0] > b[0])
      return -1;
    return 1;
  }
 
  // Function to find the parent of a node
  public static int find(int x, List<int> parent)
  {
    if (parent[x] == x)
      return x;
 
    return parent[x] = find(parent[x], parent);
  }
 
  // Function to create union of two disjoint sets
  public static bool
    union1(int x, int y, List<int> parent, List<int> rank)
  {
    int lx = find(x, parent);
    int ly = find(y, parent);
 
    // Merge their leader
    if (lx != ly) {
      if (rank[lx] > rank[ly]) {
        parent[ly] = lx;
      }
      else if (rank[lx] < rank[ly]) {
        parent[lx] = ly;
      }
      else {
        parent[lx] = ly;
        rank[ly] += 1;
      }
 
      return true;
    }
    return false;
  }
 
  // Function to find the maximum number
  // of edges that can be deleted
  public static int removeMaxEdges(int n,
                                   List<List<int> > edges)
  {
    int n1 = n + 1;
 
    // Sort on the basis on that edge
    // which is traversable by both person
    edges.Sort(cmp);
 
    // Initialize a parentA[] for person A,
    // parentB[] for person B Initialize a
    // rankA[] for person A, rankB[]
    // for person B
    List<int> parentA = new List<int>();
    List<int> parentB = new List<int>();
    List<int> rankA = new List<int>();
    List<int> rankB = new List<int>();
    for (int i = 0; i < n1; i++) {
      parentA.Add(0);
      parentB.Add(0);
      rankA.Add(0);
      rankB.Add(0);
    }
 
    // Initially every node as leader and
    // make their rank = 1.
    for (int i = 1; i <= n; i++) {
      parentA[i] = i;
      parentB[i] = i;
      rankA[i] = 1;
      rankB[i] = 1;
    }
 
    // Create variable connectedComponentA
    // to count number of connected
    // component where A can travel Create
    // variable connectedComponentB to
    // count number of connected component
    // where B can travel Create a remove
    // variable to keep track of how many
    // redundant node that need to remove.
    int connectedComponentA = n,
    connectedComponentB = n, remove = 0;
 
    // Iterate over all the edges.
    for (int i = 0; i < edges.Count; i++) {
 
      // Connect the node with edges
      // first which is traversable
      // by both
      if (edges[i][0] == 2) {
 
        // Try to merge node into DSU
        // for person A
        bool mergeA
          = union1(edges[i][1], edges[i][2],
                   parentA, rankA);
 
        // Try to merge node into DSU
        // for person B
        bool mergeB
          = union1(edges[i][1], edges[i][2],
                   parentB, rankB);
 
        // If there is merge of nodes
        // in DSU for person A. then,
        // decrement of
        // connectedComponentA by 1
        if (mergeA) {
          connectedComponentA--;
        }
 
        // If there is merge of nodes
        // in DSU for person B. then,
        // decrement of
        // connectedComponentB by 1
        if (mergeB) {
          connectedComponentB--;
        }
 
        // If there is no merge of
        // nodes in both the DSU's then,
        // this edge is redundant. So,
        // increment remove.
        if (mergeA == false && mergeB == false) {
          remove++;
        }
      }
 
      else if (edges[i][0] == 1) {
 
        // Try to merge node into DSU
        // for person A
        bool mergeA
          = union1(edges[i][1], edges[i][2],
                   parentA, rankA);
 
        // If there is merge of nodes
        // in DSU for person A.
        // then, decrement of
        // connectedComponentA by 1
        if (mergeA) {
          connectedComponentA--;
        }
 
        // If there is no merge of
        // nodes in person A's DSU then,
        // this edge is redundant. So,
        // increment remove.
        if (mergeA == false) {
          remove++;
        }
      }
 
      else {
 
        // Try to merge node into DSU
        // for person B
        bool mergeB
          = union1(edges[i][1], edges[i][2],
                   parentB, rankB);
 
        // If there is merge of nodes
        // in DSU for person B. then,
        // decrement of
        // connectedComponentB  by 1
        if (mergeB) {
          connectedComponentB--;
        }
 
        // If there is no merge of
        // nodes in person B's DSU
        // then, this edge is redundant.
        // So, increment remove.
        if (mergeB == false) {
          remove++;
        }
      }
    }
 
    // Finally check if if any one's
    // connected Component is not 1,
    // then, there is no way to travel on
    // all the node by both person.
    // So, return -1
    if (connectedComponentA != 1
        || connectedComponentB != 1) {
      return -1;
    }
 
    // Otherwise, return remove count.
    return remove;
  }
 
  // Driver code
  static public void Main()
  {
    int N = 4;
    List<List<int> > edges = new List<List<int> >{
      new List<int>{ 0, 1, 2 },
      new List<int>{ 0, 3, 4 },
      new List<int>{ 1, 1, 2 },
      new List<int>{ 1, 2, 4 },
      new List<int>{ 2, 1, 2 },
      new List<int>{ 2, 1, 3 }
    };
 
    // Function Call
    Console.WriteLine(removeMaxEdges(N, edges));
  }
}
 
// This code is contributed by ksam24000

Javascript

// JavaScript code for the above approach
 
// Function to find the parent of a node
function find(x, parent)
{
    if (parent[x] == x)
        return x;
 
    return parent[x] = find(parent[x], parent);
}
 
// Function to create union of two disjoint sets
function union1(x, y, parent, rank)
{
    let lx = find(x, parent);
    let ly = find(y, parent);
 
    // Merge their leader
    if (lx != ly) {
        if (rank[lx] > rank[ly]) {
            parent[ly] = lx;
        }
        else if (rank[lx] < rank[ly]) {
            parent[lx] = ly;
        }
        else {
            parent[lx] = ly;
            rank[ly] += 1;
        }
 
        return true;
    }
    return false;
}
 
// Function to find the maximum number
// of edges that can be deleted
function removeMaxEdges(n, edges)
{
    let n1 = n + 1;
 
    // Sort on the basis on that edge
    // which is traversable by both person
    edges.sort(function(a, b){ return b[0] - a[0] });
 
    // Initialize a parentA[] for person A,
    // parentB[] for person B Initialize a
    // rankA[] for person A, rankB[]
    // for person B
    let parentA = new Array(n1), parentB = new Array(n1),
        rankA = new Array(n1);
    rankB = new Array(n1);
 
    // Initially every node as leader and
    // make their rank = 1.
    for (let i = 1; i <= n; i++) {
        parentA[i] = i;
        parentB[i] = i;
        rankA[i] = 1;
        rankB[i] = 1;
    }
 
    // Create variable connectedComponentA
    // to count number of connected
    // component where A can travel Create
    // variable connectedComponentB to
    // count number of connected component
    // where B can travel Create a remove
    // variable to keep track of how many
    // redundant node that need to remove.
    let connectedComponentA = n, connectedComponentB = n,
        remove = 0;
 
    // Iterate over all the edges.
    for (let i of edges) {
 
        // Connect the node with edges
        // first which is traversable
        // by both
        if (i[0] == 2) {
 
            // Try to merge node into DSU
            // for person A
            let mergeA = union1(i[1], i[2], parentA, rankA);
 
            // Try to merge node into DSU
            // for person B
            let mergeB = union1(i[1], i[2], parentB, rankB);
 
            // If there is merge of nodes
            // in DSU for person A. then,
            // decrement of
            // connectedComponentA by 1
            if (mergeA) {
                connectedComponentA--;
            }
 
            // If there is merge of nodes
            // in DSU for person B. then,
            // decrement of
            // connectedComponentB by 1
            if (mergeB) {
                connectedComponentB--;
            }
 
            // If there is no merge of
            // nodes in both the DSU's then,
            // this edge is redundant. So,
            // increment remove.
            if (mergeA == false && mergeB == false) {
                remove++;
            }
        }
 
        else if (i[0] == 1) {
 
            // Try to merge node into DSU
            // for person A
            let mergeA = union1(i[1], i[2], parentA, rankA);
 
            // If there is merge of nodes
            // in DSU for person A.
            // then, decrement of
            // connectedComponentA by 1
            if (mergeA) {
                connectedComponentA--;
            }
 
            // If there is no merge of
            // nodes in person A's DSU then,
            // this edge is redundant. So,
            // increment remove.
            if (mergeA == false) {
                remove++;
            }
        }
 
        else {
 
            // Try to merge node into DSU
            // for person B
            let mergeB = union1(i[1], i[2], parentB, rankB);
 
            // If there is merge of nodes
            // in DSU for person B. then,
            // decrement of
            // connectedComponentB  by 1
            if (mergeB) {
                connectedComponentB--;
            }
 
            // If there is no merge of
            // nodes in person B's DSU
            // then, this edge is redundant.
            // So, increment remove.
            if (mergeB == false) {
                remove++;
            }
        }
    }
 
    // Finally check if if any one's
    // connected Component is not 1,
    // then, there is no way to travel on
    // all the node by both person.
    // So, return -1
    if (connectedComponentA != 1
        || connectedComponentB != 1) {
        return -1;
    }
 
    // Otherwise, return remove count.
    return remove;
}
 
// Driver code
let N = 4;
let edges = [
    [ 0, 1, 2 ], [ 0, 3, 4 ], [ 1, 1, 2 ], [ 1, 2, 4 ],
    [ 2, 1, 2 ], [ 2, 1, 3 ]
];
 
// Function Call
console.log(removeMaxEdges(N, edges));
// This code is contributed by Potta Lokesh

Python3

from functools import cmp_to_key
 
def cmp(a, b):
    return a[0] > b[0]
#Function to find the parent of a node
def find(x, parent):
    if parent[x] == x:
        return x
 
    parent[x] = find(parent[x], parent)
    return parent[x]
#Function to create union of two disjoint sets
def union1(x, y, parent, rank):
    lx = find(x, parent)
    ly = find(y, parent)
#Merge their leader
    if lx != ly:
        if rank[lx] > rank[ly]:
            parent[ly] = lx
        elif rank[lx] < rank[ly]:
            parent[lx] = ly
        else:
            parent[lx] = ly
            rank[ly] += 1
        return True
 
    return False
#Function to find the maximum number of edges that can be deleted
def removeMaxEdges(n, edges):
    n1 = n + 1
    # Sort on the basis on that edge
    # which is traversable by both person
    edges.sort(key=cmp_to_key(cmp))
#Initialize a parentA[] for person A,
    # parentB[] for person B Initialize a
    # rankA[] for person A, rankB[]
    # for person B
    parentA, parentB = [0] * n1, [0] * n1
    rankA, rankB = [0] * n1, [0] * n1
#Initially every node as leader and
# make their rank = 1.
    for i in range(1, n1):
        parentA[i] = i
        parentB[i] = i
        rankA[i] = 1
        rankB[i] = 1
 
 
 #Create variable connectedComponentA
# to count number of connected
# component where A can travel Create
# variable connectedComponentB to
# count number of connected component
# where B can travel Create a remove
# variable to keep track of how many
# redundant node that need to remove.
    connectedComponentA, connectedComponentB = n, n
    remove = 1
 
    for i in edges:
        # Connect the node with edges
      # first which is traversable
      # by both
        if i[0] == 2:
            mergeA = union1(i[1], i[2], parentA, rankA)
            mergeB = union1(i[1], i[2], parentB, rankB)
    # Try to merge node into DSU
        # for person A
            if mergeA:
                connectedComponentA -= 1
    # Try to merge node into DSU
        # for person B
            if mergeB:
                connectedComponentB -= 1
 
            if not mergeA and not mergeB:
                remove += 1
 
        elif i[0] == 1:
            mergeA = union1(i[1], i[2], parentA, rankA)
  # If there is merge of nodes
        # in DSU for person A. then,
        # decrement of
        # connectedComponentA by 1
            if mergeA:
                connectedComponentA -= 1
 
            if not mergeA:
                remove += 1
 
        else:
            mergeB = union1(i[1], i[2], parentB, rankB)
 
            if mergeB:
                connectedComponentB -= 1
 
            if not mergeB:
                remove += 1
    # Finally check if if any one's
    # connected Component is not 1,
    # then, there is no way to travel on
    # all the node by both person.
    # So, return -1
    if connectedComponentA != 1 or connectedComponentB != 1:
        return -1
 
    return remove
if __name__ == '__main__':
    N = 4
    edges = [[0, 1, 2], [0, 3, 4], [1, 1, 2], [1, 2, 4], [2, 1, 2], [2, 1, 3]]
 
    # Function Call
    print(removeMaxEdges(N, edges))

Output

2

Time Complexity: O(E * log(N) + E), where E, and N are the number of edges and number of nodes respectively.
Auxiliary Space: O(N)


 


Reffered: https://www.geeksforgeeks.org

Graph

Related
Check if all nodes of Undirected Graph can be visited from given Node Check if all nodes of Undirected Graph can be visited from given Node
Minimize rope length to connect given points in a 3D plane Minimize rope length to connect given points in a 3D plane
Edge Relaxation Property for Dijkstra’s Algorithm and Bellman Ford&#039;s Algorithm Edge Relaxation Property for Dijkstra’s Algorithm and Bellman Ford&#039;s Algorithm
Count of Disjoint Groups by grouping points that are at most K distance apart Count of Disjoint Groups by grouping points that are at most K distance apart
Check if we can visit all other nodes from any node in given Directed Graph Check if we can visit all other nodes from any node in given Directed Graph

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 13



 

Horje