A square prism is a three-dimensional-shaped geometric structure that has two congruent square bases that are connected by four rectangular faces. A prism having a square base is defined as a square prism.

In this article, we will learn about, the Square Prism definition, the Volume of the Square Prism Formula, and others in detail.

What is a Square Prism?

A square prism has a total of six faces (two square bases and four rectangular faces), twelve edges, and eight vertices. The lateral faces (or) sides faces are rectangles, and the two bases are squares, the area of prism is the total area of all its faces. Depending upon the alignment of the square bases, a square prism is classified into two types, a right square prism, and an oblique square prism. Right square prisms have lateral faces that are perpendicular to their square bases, whereas oblique square prisms have lateral faces that aren’t perpendicular to the square bases.

The image of a square prism is added below:

Square Prism

Volume of Square Prism

Volume of a square prism is the total amount of space that is enclosed by the prism. The volume or capacity is in terms of cubic units and is equal to the product of the base area and the height.

Formula for calculating the volume of any prism is given as follows:

Volume of a prism (V) = Base Area × Height of Prism

Volume of Square Prism Formula

Formula for finding the volume of a square prism is base multiplied by area. Now, the two congruent bases of the prism are squares. 

Hence, the base area = (edge)² = a² square units

Now, substitute the values in the above formula, we get

Volume of a Square Prism = a²h cubic units

Where,

• “a” is Side of Square Base
• “h” is Height of Square Prism

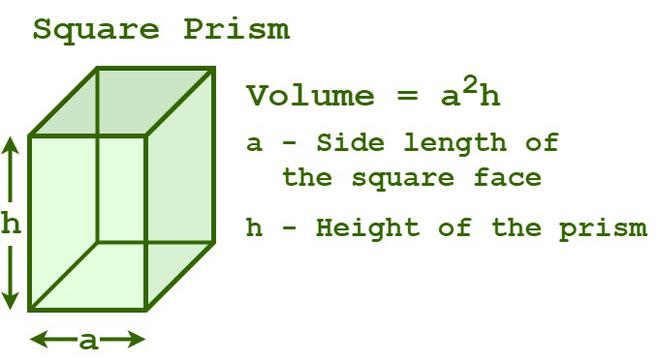Volume of Square Prism Formula

How To Calculate Volume of Square Prism?

Steps to Calculate the Volume of Square Prism are explained below:

Step 1: 

Write the given dimensions of the square prism. Now s = side of square prism, s² = area of the base, and h = height of square prism.
Make sure that the units of s and h should be the same.

Step 2: 

Put these respective values in the volume of square prism formula s²h.

Step 3: 

The value obtained is the volume of the square prism. Write the unit of the volume of the square prism is in terms of units³.

Consider the following example:

Example: Find the volume of a square prism if the edge of the base is 9 and its height is 11.

Solution:

Given data,

• Edge of base = 9
• Height of a square prism (h) = 11

We have,

Volume of a Square Prism = Base Area × Height of Prism

By substituting the values in the formula, we get

= 9² × 11 = 891 cu. units

Therefore, the volume of a square prism is 891 cu. units.

Examples on Volume of a Square Prism

Example 1: Calculate the volume of a square prism whose side is 10 inches and whose height is 15 inches.

Solution:

Given data,

• Length of the side of a square prism (a) = 10 inches
• Height of a square prism (h) = 15 inches

We have,

Volume of a square prism = a²h cubic units

= (10)² × 15

= 100 × 15 = 1500 cu. in

Thus, the volume of the given prism is 1500 cu. in.

Example 2: Find the volume of a square prism if the length of the side of the square face of a square prism is 12 cm and its height is 17 cm.

Solution:

Given data,

• Length of the side of a square prism (a) = 12 cm
• Height of a square prism (h) = 17 cm

We have,

Volume of a square prism = a²h cubic units

= (12)² × 17

= 144 × 17 = 2448 cu. cm

Therefore, the volume of a square prism is 2448 cu. cm.

Example 3: Determine the volume of a square prism whose length of the side of the square face is 8 units and whose height is 10 units.

Solution:

Given data,

• Length of the side of a square prism (a) = 8 units
• Height of a square prism (h) = 10 units

We have,

Volume of a square prism = a²h cubic units

Now, substitute the values of a and h in the formula.

= (8)² × 10

= 64 × 10 = 640 cubic units

Thus, the volume of the given prism is 640 cubic units.

Example 4: Find the length of the edge of the square prism if the volume of the square prism is 1,694 cu. cm and the height is 14 cm. 

Solution:

Given data,

• Height of a square prism (h) = 14 cm
• Volume of a square prism = 1694 cu. cm

We have,

Volume of a square prism = a²h cubic units

By substituting the values in the formula, we get

⇒ 1694 = (a²) × (14)

⇒  a² = 1694 ÷ 14 = 121

⇒ a = √121 = 11 cm

Thus, the length of the edge of the square prism is 11 cm.

FAQs on Volume of a Square Prism

What is Formula for Volume of a Square Prism?

Formula for the volume of square prism is (Base Area) × (Height of Square Prism).

What is the Square Prism?

Square prism is a 3-D shape whose bases are squares and the other four faces are rectangle in shape.

What is Formula for Finding Volume of a Square Prism?

A square prism is a prism whose base is in the shape of a square. Volume of square prism is given by the formula:

Volume of a Square Prism = a²h cubic units

What happens to Volume of a Square Prism if Height of Square Prism is Doubled?

We know that the formula for calculating the volume of any prism is (Base Area) × (Height of Prism). We can clearly say that the volume of the prism is directly proportional to its height. So, as the height of the square prism is doubled, its volume will also be doubled.

What happens to Volume of a Square Prism if Length of Square Face is Reduced to Half?

Formula for calculating the volume of a square prism.

V = a²h cubic units. 

Volume of prism is directly proportional to the square of the length of edge of square face.

V’ = (a/2)²h = (a²h)/4 = V/4

So, the new volume of the square prism is one-fourth of its old volume.