Number of Sides	Name of Polygon	Figure
3	Triangle	Triangle
4	Quadrilateral	Quadrilateral
5	Pentagon	Pentagon
6	Hexagon	Hexagon
7	Heptagon	Heptagon
8	Octagon	Octagon
9	Nonagon	Nonagon
10	Decagon	Decagon

Based on measure of angles and the sides of a polygon, they are classified into the following types

1. Regular polygon
2. Irregular polygon
3. Concave polygon
4. Convex polygon
5. Equilateral polygon
6. Equiangular Polygon

Regular Polygon

A polygon is said to be a regular polygon if it has all the interior angles and the sides are of the same measure. The regular polygon are shown in the image added below:

Irregular Polygon

A polygon is said to be a irregular polygon if it has all the interior angles and the sides have different values. The irregular polygon are shown in the image added below: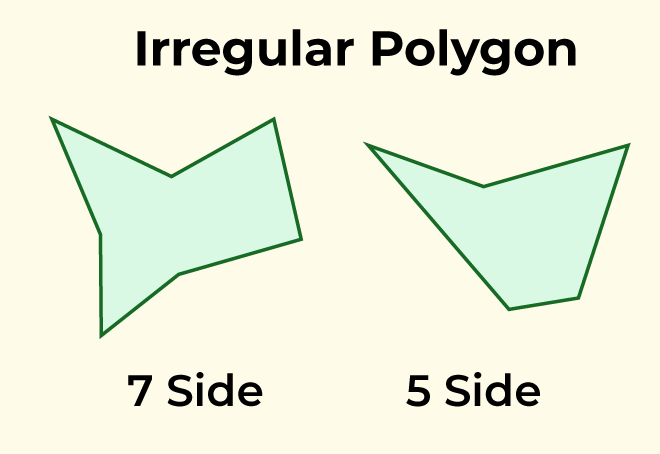

Concave Polygon

A concave polygon is a polygon that has at least one interior angle greater than 180 degrees, i.e., a reflex angle. The concave polygon are shown in the image added below:

Convex Polygon

A convex polygon is a polygon that has all the interior angles of a polygon less than 180 degrees. The convex polygon are shown in the image added below:

Equilateral Polygon

An equilateral polygon is a polygon whose all sides measure the same.

Equiangular Polygon

An equiangular polygon is a polygon whose all angles measure the same.

Properties of Polygon

Various properties of polygon are:

• Sum of the interior angles of a polygon depends on the number of sides.

• Number of vertices in a polygon is equal to the number of sides.

• Sum of the exterior angles in any polygon is always 360 degrees.

• A polygon can be either convex (all interior angles are less than 180 degrees) or concave (at least one interior angle is greater than 180 degrees).

• A polygon is regular if all its sides and angles are congruent (equal); otherwise, it’s irregular.

Article Related to Polygon Formula:

• Acute Angled Triangle
• Right Angled Triangle:
• Obtuse Angled Triangle
• Polyhedrons
• Diagonal of Polygon

Solved Examples on Polygon Formula

Let’s solve some example problems based on the Polygon Formulas.

Example 1: Calculate the perimeter and value of one interior angle of a regular heptagon whose side length is 6 cm.

Solution:

Polygon is an heptagon. So, number of sides (n) = 7

Length of each side (s) = 6 cm

We know that,

Perimeter of the heptagon (P) = n × s

P = 7 × 6

  = 42 cm

Now, find each interior angle by using the polygon formula,

Interior Angle = [(n-2)180°]/n

= [(7 – 2)180°]/7

= (5 × 180°)/7

= 128.57°

Therefore, perimeter of the given heptagon is 42 cm and the value of each internal angle is 128.57°.

Example 2: Calculate the measure of one interior angle and the number of diagonals of a regular decagon.

Solution:

Polygon is a decagon. So, number of sides (n) = 10

Now, to find each interior angle by using the polygon formula,

Interior Angle = [(n-2)180°]/n

= [(10 – 2)180°]/10

= (8 × 180°)/10

= 144‬°

We know that,

Number of diagonals in a n-sided polygon = n(n-3)/2

= 10(10 – 3)/2

= 10(7)/2 = 35.

Therefore, value of each internal angle of a regular decagon is 144° the number of diagonals is 35. 

Example 3: Calculate the sum of interior angles of a hexagon using the polygon formula.

Solution:

Polygon is a hexagon. So, number of sides (n) = 6

We know that,

Sum of interior angles of a polygon = (n-2)×180°

= (6-2)×180°

= 4×180° = 720°.

Hence, sum of interior angles of a hexagon is 720°.

Example 4: Calculate the measures of one exterior angle and the perimeter of a regular pentagon whose side length is 9 inches.

Solution:

Polygon is a pentagon. So, number of sides (n) = 5

We know that,

Length of each side (s) = 9 inches

We know that,

Perimeter of the pentagon (P) = n × s

P = 5 × 9

 = 45 inches

Each exterior angle of a regular polygon = 360°/n

=  360°/5 = 72°.

Hence, measures of one exterior angle and the perimeter of a regular pentagon are 72° and 45 inches, respectively.

Polygon Formulas- FAQs

What do we mean by the Polygon?

Polygon is a 2-D closed structure that is made up of three or more straight lines. A polygon consists of a minimum of three sides. Each line segment intersects with another line segment only at the vertex of Polygon. Polygon can be classified on the basis of angles. Some examples of polygons are triangles, squares, pentagons, hexagons, etc.

How Many Types of Polygon are there?

On the basis of the measurement of angles and the sides of a polygon, a polygon can be classified into:

• Regular Polygon: The interior angles and the sides of the polygon are equal.
• Irregular Polygon: The interior angles and the sides of the polygon are not equal.
• Convex polygon: The interior angles of a polygon are strictly less than 180°.
• Concave Polygon: Polygons have one or more interior angles which are greater than 180°.

What are Properties of a Polygon?

Some important properties of the polygon are:

• Sum of all the exterior angles of a polygon is always equal to 360°
• If at least one of the interior angles of a polygon is greater than180°, it is termed a concave polygon.
• If all the angles of a polygon are less than 180° then it is a convex polygon.

What are the Polygon from 1 to 20?

Names of polygons with sides ranging from 1 to 20 are added in table below: