|
|
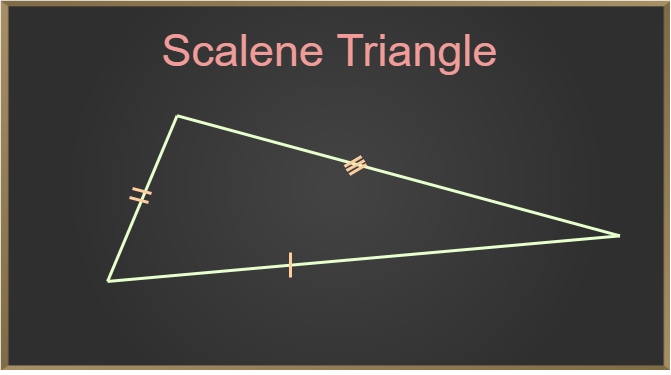
A triangle is one of the simplest shapes in geometry, consisting of three sides and three angles. Among the various types of triangles, the scalene triangle stands out because it has unique properties that distinguish it from others. In a scalene triangle, all three sides have different lengths, and all three angles are different. Scalene Triangle is defined as a type of triangle whose all sides and angles are unequal. It follows the angle sum property of the triangle. This lack of symmetry makes scalene triangles interesting and a bit more challenging to study compared to other types of triangles, like equilateral or isosceles triangles. Let’s discuss the properties, formula, and example problems on the Scalene triangle. Table of Content Scalene Triangle Definition
It is to be noted that the angles in the scalene triangle follow the angle sum property of the triangle, i.e. the sum of all the different angles of the triangle is always 180°. In a scalene triangle, all the angles are also unequal. The triangle added in the image below has unequal sides and unequal angles hence, it is a Scalene Triangle.
Read More about Triangles. Classification of TrianglesWe can classify the triangles into various categories by comparing their sides and interior angles. Here is the basic classification of the triangle: On the basis of the measure of interior angles, different types of triangles are, On the basis of the measure of the side of the triangles, they are categorized into three types, which include,
Scalene Triangle TypesScalene triangles are based on the measure of their interior angles. They can be further classified into three categories that are,
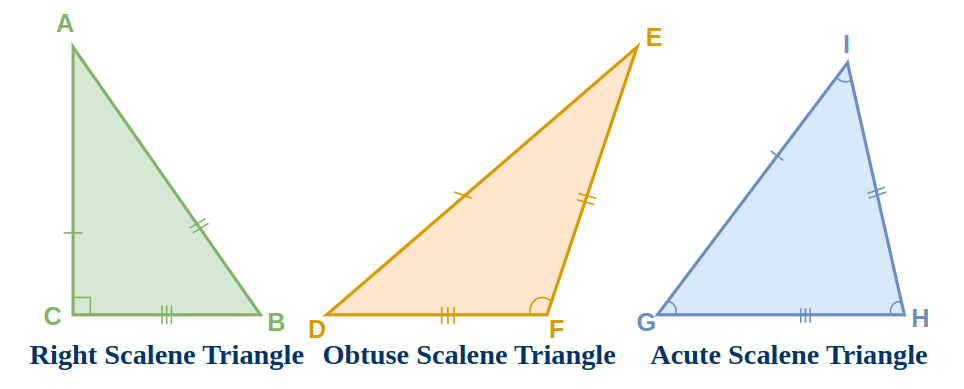
Now let’s learn about them in detail. Acute-Angled Scalene TriangleAn acute-angled scalene triangle is a scalene triangle in which all the interior angles of the triangle are acute angles. I Obtuse-Angled Scalene TriangleAn obtuse-angled scalene triangle is a scalene triangle in which any one of the interior angles of the triangle is an obtuse angle(i.e. its measure is greater than 90°). The other two angles are acute angles. Right-Angled Scalene TriangleA right-angled scalene triangle is a scalene triangle in which any one of the interior angles of the triangle is a right angle (i.e. its measure is 90°). The other two angles are acute angles. Properties of Scalene TriangleKey properties of a scalene triangle are,
Difference between Scalene, Equilateral and Isosceles TrianglesThe main differences between Scalene, Equilateral and Isosceles Triangles are tabulated below:
Read More On: Scalene Triangle FormulaA triangle with no two sides equal is called a scalene triangle. A scalene triangle has two major formulas
Let’s discuss these two formulas in detail. Scalene Triangle PerimeterPerimeter of any figure is the length of its total boundary. So, the perimeter of a scalene triangle is defined as the sum of all of its three sides.
From the above figure,
Scalene Triangle AreaArea of any figure is the space enclosed inside its boundaries for the scalene triangle area is defined as the total square unit of space occupied by the Scalene triangle. Area of the scalene triangle depends upon its base and height of it. The image added below shows a scalene triangle with sides a, b and c and height h units.
When Base and Height are GivenWhen the base and the height of the scalene triangle is given then its area is calculated using the formula added below,
When Sides of a Triangle are GivenIf the lengths of all three sides of the scalene triangle are given instead of base and height, we calculate the area using Heron’s formula, which is given by,
Read More, Scalene Triangle ExamplesLet us solve some questions on scalene triangles and their properties. Example 1: Find the perimeter of a scalene triangle with side lengths of 10 cm, 15 cm, and 6 cm. Solution:
Example 2: Find the length of the third side of a scalene triangle with two side lengths of 3 cm and 7 cm and a perimeter of 20 cm. Solution:
Example 3: Find the area of a scalene triangle with side lengths of 8 cm, 6 cm, and 10 cm. Solution:
Example 4: Find the area of a scalene triangle whose base is 20 cm and altitude is 10 cm. Solution:
Scalene Triangle Practice QuestionsHere is a list of questions on scalene triangle for your practice. Q1: Find Area of a Scalene Triangle with base is 24 cm and altitude is 16 cm. Q2: Find the area of Scalene Triangle with sides, 3 cm, 4 cm and 5 cm. Q3: Find the perimeter of the scalene triangle with sides, 10 cm, 11 cm, 13, cm. Q4: Check weather they are Scalene Triangle or not if the sides are,
Scalene Triangle- FAQsWhat is Scalene Triangle in Geometry?
Can Scalene Triangles be Obtuse?
What are Properties of Scalene Triangle?
How to find the Area of Scalene Triangle?
What is the perimeter formula of Scalene Triangle?
Does the angle sum property hold true for scalene triangle?
What is Right Scalene Triangle?
What is Acute Scalene Triangle?
What is Scalene vs Obtuse Triangle?
|
Reffered: https://www.geeksforgeeks.org
| Mathematics |
| Related |
|---|
| |
| |
| |
| |
| |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 11 |




