Chain Rule is a way to find the derivative of composite functions. It is one of the basic rules used in mathematics for solving differential problems. It helps us to find the derivative of composite functions such as (3x² + 1)⁴, (sin 4x), e³x, (ln x)², and others. Only the derivatives of composite functions are found using the chain rule. The famous German scientist, Gottfried Leibniz gave the chain rule in the early 17^th century.

Let’s learn about Chain Rule formula, derivation and examples in detail below.

What is Chain Rule?

Chain rule is a method to find derivative of Composite Function. It states that the derivative of composite function f(g(x)) is f'(g(x))⋅ g'(x). In other words, Cos(4x), is a composite function and it can be written as f(g(x)) where f(x) = Cos(x) and g(x) = 4x.

We can then compute the derivative of Cos(4x) using the chain rule and the derivatives of Cos(x) and 4x.

Chain Rule Theorem

We are going to discuss Chain Rule Theorem in this section.

For any real-valued function f which is a composite of the other two real functions p(x) and q(x) such that f = p o q

Then the rate of change of f with respect to t is expressed as,

Rate of change of f with respect to t = Rate of change of p with respect to u × Rate of change of u with respect to t i.e.

 df/dt = dp/du . du/dt

Chain Rule Steps to find the Derivative

We have explained the steps to find the derivative of Chain Rule. Below is the steps to find the derivative of function Sin(x²).

Step 1: Check to see if the function is a composite function, meaning it comprises a function within a function. The function Sin(x2) is a composite function.

Step 2: Determine the outer f(x) and inner functions g(x). f(x) = Sin(x) and g(x) = x² in this case.

Step 3: Now only look for the differentiation of the outer function. In this case, f'(x) = Cos (x).

Step 4: Now only look for the differentiation of the inner function. In this case, g'(x) = 2x.

Step 5: Find the product of f'(x) and g'(x) here, which is (2x)Cos(x).

We found the derivative of Sin(x²), which is (2x)Cos using the Chain rule (x).

Chain Rule Formula

There are two forms of chain rule of differentiation formula as shown below: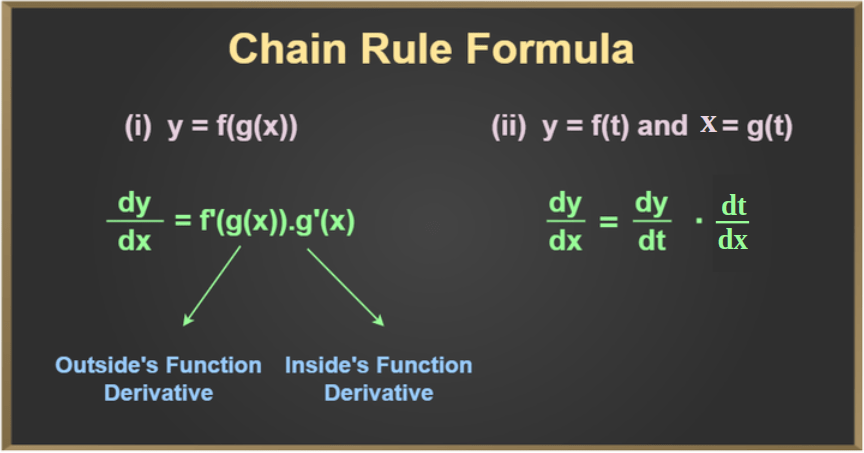

Chain Rule Formula 1: d/dx ( f(g(x) ) = f’ (g(x)) · g’ (x)

Let’s understand the first Chain Rule Formula with the help of an example:

Example: Find the derivative of d/dx (cos 2x)

Solution:

Let cos 2x = f(g(x)), then f(x) = cos x and g(x) = 2x.

Then by the chain rule formula,

d/dx (cos 2x) = -sin 2x · 2 

                    = -2 sin 2x

Chain Rule Formula 2: dy/dx = dy/du · du/dx

Let’s understand the second Chain Rule Formula with the help of an example:

Example: Find d/dx (cos 2x)

Solution:

Let y = cos 2x and 2x = u. Then y = cos u

By the chain rule formula,

d/dx (cos 2x) = d/du (cos u) · d/dx(2x) 

                     = -sin u · 2 = -2 sin u 

                     = -2 sin 2x

Chain Rule Formula Proof

Now we are going to discuss the proof of Chain Rule Formula.

As per Leibniz’s differential notation, we can treat derivatives as fractions i.e. for y = f(x), f'(x) can be treated as dy/dx.

Therefore, 

For a composite function, dy/dx = (dy/du) × (du/dx)

To justify this with a better notation, let us arrive at the result, starting with the definition of the derivative.

Given: y = f(u(x)).

From earlier, we know that, dy/dx = (dy/du) × (du/dx).

Then,

Now, we know that a function which is differentiable at a point c is also continuous at the point c i.e.

∆ u ⇢ 0 as  ∆ x ⇢ 0 

Then, 

= f'(g(x)). g'(x)

This is the Chain Rule. Hence, the Chain Rule has been proved.

Double Chain Rule of Differentiation

We are going to learn Double Chain Rule of Differentiation.

For a function where it is dependent on more than one variable. i.e. the nesting of function occurs, chain rule of differentiation fails in such a situation double chain rule is applied.

Now for any three functions p, q, and r and a composite function f where f is a composite of p, q, and r such that, f = (p o q) o r, i.e. f(x) = p[q{r(x)}], then its derivative is given as,

df/dx = df/dp. dp/dq. dq/dr. dr/dx

Let’s understand the Double Chain Rule with the help of an example :

Example: Differentiate, y = (sin 2x)²

Solution:

y = (sin 2x)²

y’ = 2( sin 2x) . (cos 2x). (2)

    = 4 sin2x . cos 2x

Chain Rule for Partial Derivatives

The concept of chain rule also works for partial derivatives. Partial derivatives are found when in the differentiation of any function one or more variable is kept constant with respect to the differentiating variable. The chain Rule for Partial Derivatives uses the concept of the Jacobian matrix.

Thus, the chain rule for the partial derivatives of the function y = f(u) = (f₁(u), …, f_k(u)) and u = g(x) = (g₁(x), …, g_m(x)) can be written as,

∂(y₁,……,y_k) / ∂x_i = ∂(y₁,……,y_k) / ∂(u₁,……,u_m) × ∂(u₁,……,u_m) /  ∂x_i

Application of Chain Rule

This chain rule is widely used in mathematics to find the differentiation of complex functions. Some of its uses are discussed below,

• For finding the rate of change of the pressure with respect to time.
• For finding the rate of change of the average molecular speed.
• To determine if the given function is increasing or decreasing.
• For finding the rate of change of distance between two moving objects,

Must Read

• Differentiation and Integration Formula
• Advanced Differentiation
• Implicit Differentiation

Chain Rule Derivative Solved Examples

Listed below are a few solved examples on Chain Rule to enhance your understanding of the concept:

Chain Rule Example 1: Solve, y(x) = (2x²+ 8)²

Solution:

Here, as you can see that y(x) is a composite function. 

So it can be written as f(g(x)). The outer function f(g(x)) is g(x)² and the inner function g(x) is 2x² + 8.

So, f'(g(x)) = 2g(x), here g(x) = 2x²+ 8. 

Therefore, 

f'(g(x)) = 2(2x² + 8) and g'(x) = 4x.

Now 

y'(x) = f'(g(x)).g'(x) 

       = 2(2x² + 8)(4x) 

       = 16x(x² + 4).

Chain Rule Example 2: Solve, y(x) = Cos(4x).

Solution:

Here, as we know from earlier, y(x) is a composite function. 

So it can be written as f(g(x)). The outer function f(g(x)) is Cos(g(x)) and the inner function g(x) is 4x.

So, f'(g(x)) = -Sin(g(x)), here g(x) = 4x. 

Therefore, 

f'(g(x)) = -Sin(4x) and g'(x) = 4.

Now 

y'(x) = f'(g(x)).g'(x) 

       = -(Sin(4x))(4) 

       = -4Sin(4x).

Chain Rule Example 3: Solve, y(x) = ln(x² – 1).

Solution:

Here, as we know from earlier, y(x) is a composite function. 

So it can be written as f(g(x)). The outer function f(g(x)) is ln(g(x)) and the inner function g(x) is x² – 1.

So, f'(g(x)) = 1/(g(x)), here g(x) = x² – 1. 

Therefore, 

f'(g(x)) = 1/(x² – 1) and g'(x) = 2x.

Now 

y'(x) = f'(g(x)).g'(x) 

        = (1/(x² – 1))(2x) 

        = 2x/(x² – 1).

Chain Rule Example 4: Solve, y(x) = (ln x)².

Solution:

Here, as we know from earlier, y(x) is a composite function. 

So it can be written as f(g(x)). The outer function f(g(x)) is (g(x))² and the inner function g(x) is ln x.

So, f'(g(x)) = 2g(x) , here g(x) = ln x. 

Therefore, 

f'(g(x)) = 2(ln x) and g'(x) = 1/x.

Now 

y'(x) = f'(g(x)).g'(x) 

       = (2(ln x))(1/x) 

       = 2(ln x)/(x).

Chain Rule Example 5: Solve, y(x) = √(x³ + 56).

Solution:

Here, as we know from earlier, y(x) is a composite function. So it can be written as f(g(x)). The outer function f(g(x)) is √(g(x)) and the inner function g(x) is x³ + 56.

So, f'(g(x)) = (1/2)(x³ + 56)^-1/2, here g(x) = x³ + 56. 

Therefore, 

f'(g(x)) = (1/2)(x³ + 56)^-1/2 and g'(x) = 3x²

Now 

y'(x) = f'(g(x)).g'(x) 

        = ( (1/2)(x³ + 56)^-1/2) × ( 3x²) 

        = [(3/2) x²] / (x³ + 56)1/2.

Chain Rule Example 6: Solve, y(x) = ln √x.

Solution:

Here, as we know from earlier, y(x) is a composite function. 

So it can be written as f(g(x)). The outer function f(g(x)) is ln(g(x)) and the inner function g(x) is √x.

So, f'(g(x)) = 1/g(x), here g(x) = √x. 

Therefore, 

f'(g(x)) = 1/(√x) and g'(x) = (1/(2√x)).

Now 

y'(x) = f'(g(x)).g'(x) 

        = (1/(√x))(1/(2√x)) 

        = 1/2x

Chain Rule Derivative Practice Problems

Here are some practice problems on Chain Rule fo you to solve:

1. Find the derivative of f(x) = sin(3x).

2. Calculate the derivative of f(x) = ln(2x² + 1).

3. Determine the derivative of f(x) = e^(2×3).

4. Find the derivative of f(x) = (4x² + 1)⁵

5. Calculate the derivative of f(x) = √(3x – 1).

6. Determine the derivative of f(x) = cos(2x² – 1).

Chain Rule Differential – FAQs

What is Chain Rule?

Chain rule helps us to find the derivative of composite functions. For any given composite function y = f(g(x)) its derivative is calculated as,

y’ = f'(g(x)). g'(x)

What is Chain Rule Formula?

The chain rule has two formulas which are used to solve composite functions which include,

• d/dx ( f(g(x) ) = f’ (g(x)) · g’ (x)
• dy/dx = dy/du · du/dx

When to use Chain Rule Formula?

The chain rule is used when we have to find the differentiation of composite functions such as, chain rule gives differentiation of function such as (ln x)², etc.

What is the difference between the Chain Rule Formula and the Product Rule?

The chain rule formula is used to differentiate a composite function such as (ln x)², (x² + 1)³ and others, whereas the product rule is used to find the derivative of the product of two functions, such as sin x · ln x, x².ln x, and others.