Horje
Maximum sum of distances of a node to every other node

Given an undirected, connected tree with N nodes valued from 0 to N – 1 and an array edges[][2] represents the edges between two nodes, the task is to find the maximum sum of distances of a node to every other node in the tree.

Examples:

Input: N = 5, edges = { {0, 2}, {1, 3}, {0, 1}, {3, 4} }

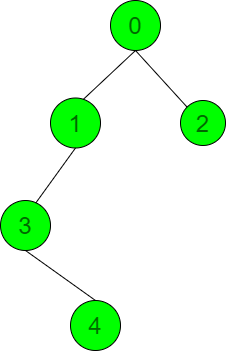
Output: 10
Explanation:
Considering the node 2 as the sources node, the distances of all other nodes from node 2 are: 1(node 0), 2(node 1), 3(node 3), 4(node 4). Therefore, the sum of distances is 1 + 2 + 3 + 4 = 10.

Input: N = 6, edges[][] = {{0, 1}, {0, 2}, {2, 3}, {2, 4}, {2, 5}}

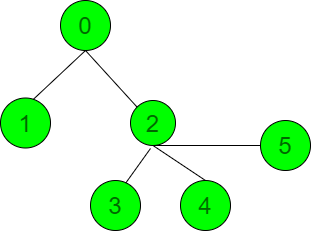
Output: 12

Naive Approach: The simplest approach to solve the given problem is to perform the Depth First Search Traversal from every node and find the sum of distance every other node from the current source node. After checking from all the nodes as the source node print the maximum sum among all the sum of values obtained.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to perform DFS and find the
// distance from a node to every other
// node
void dfs(int s, vector<vector<int> > g,
         int p, int d, int& ans)
{
    for (int i : g[s]) {
 
        // If i is not equal to
        // parent p
        if (i != p) {
            ans += d;
            dfs(i, g, s, d + 1, ans);
        }
    }
}
 
// Function to find the maximum sum of
// distance from a node to every other
// node
void maxPotentialDistance(
    int N, vector<vector<int> >& edges)
{
    int ans = 0;
 
    // Construct the graph
    vector<vector<int> > g(N, vector<int>());
 
    for (auto& it : edges) {
        g[it[0]].push_back(it[1]);
        g[it[1]].push_back(it[0]);
    }
 
    // Find the sum of distances from
    // every node
    for (int i = 0; i < N; i++) {
 
        // Stores the maximum sum of
        // distance considering the
        // current node as source node
        int a = 0;
 
        // Perform DFS Traversal to
        // find the sum of distances
        dfs(i, g, -1, 1, a);
 
        // Update the maximum sum
        ans = max(ans, a);
    }
 
    // Print the maximum sum
    cout << ans;
}
 
// Driver Code
int main()
{
    int N = 6;
    vector<vector<int> > edges = {
        { 0, 1 }, { 0, 2 }, { 2, 3 }, { 2, 4 }, { 2, 5 }
    };
 
    maxPotentialDistance(N, edges);
 
    return 0;
}

Java

// Java program for the above approach
 
import java.util.*;
 
class GFG
{
 
  // Function to perform DFS and find the
  // distance from a node to every other
  // node
  static void dfs(int s, List<List<Integer>> g, int p, int d, int[] ans) {
    for (int i : g.get(s))
    {
 
      // If i is not equal to
      // parent p
      if (i != p) {
        ans[0] += d;
        dfs(i, g, s, d + 1, ans);
      }
    }
  }
 
  // Function to find the maximum sum of
  // distance from a node to every other
  // node
  static void maxPotentialDistance(int N, List<List<Integer>> edges) {
    int[] ans = { 0 };
 
    // Construct the graph
    List<List<Integer>> g = new ArrayList<>();
    for (int i = 0; i < N; i++) {
      g.add(new ArrayList<>());
    }
    for (List<Integer> it : edges) {
      g.get(it.get(0)).add(it.get(1));
      g.get(it.get(1)).add(it.get(0));
    }
 
    // Find the sum of distances from
    // every node
    for (int i = 0; i < N; i++)
    {
 
      // Stores the maximum sum of
      // distance considering the
      // current node as source node
      int[] a = { 0 };
 
      // Perform DFS Traversal to
      // find the sum of distances
      dfs(i, g, -1, 1, a);
 
      // Update the maximum sum
      ans[0] = Math.max(ans[0], a[0]);
    }
 
    // Print the maximum sum
    System.out.println(ans[0]);
  }
 
  // Driver Code
  public static void main(String[] args) {
    int N = 6;
    List<List<Integer>> edges = Arrays.asList(
      Arrays.asList(0, 1),
      Arrays.asList(0, 2),
      Arrays.asList(2, 3),
      Arrays.asList(2, 4),
      Arrays.asList(2, 5)
    );
    maxPotentialDistance(N, edges);
  }
}
 
// This code is contributed by poojaagarwal2.

Python3

# python program for the above approach
 
pd_0 = 0
 
# Function to perform DFS and find the
# distance from a node to every other
# node
 
 
def dfs(s, g, p, d, count):
    global pd_0
    for i in g[s]:
 
                # If i is not equal to
                # parent p
        if (i != p):
            pd_0 += d
 
            # Perform the DFS Traversal
            dfs(i, g, s, d + 1, count)
 
            # Update the count of
            # nodes
            count[s] = count[s] + count[i]
 
 
# Function to find the distances from
# every other node using distance from
# node 0
def dfs2(s, g, p, pd_all, n, count):
 
    for i in g[s]:
 
                # If i is not equal to the
                # parent p
        if (i != p):
            pd_all[i] = pd_all[s] - count[i] + n - count[i]
            dfs2(i, g, s, pd_all, n, count)
 
 
# Function to find the maximum sum of
# distance from a node to every other
# node
def maxPotentialDistance(N, edges):
    global pd_0
    ans = 0
 
    # Construct the graph
    g = [[] for _ in range(N)]
 
    for it in edges:
        g[it[0]].append(it[1])
        g[it[1]].append(it[0])
 
        # Stores the number of nodes in
        # each subtree
 
    count = [1 for _ in range(N)]
 
    # Find the sum of distances from
    # node 0 and count the number of
    # nodes in each subtree
 
    dfs(0, g, -1, 1, count)
 
    # Stores distances from each node
    pd_all = [0 for _ in range(N)]
    pd_all[0] = pd_0
 
    # Find the distances from each
    # node using distance from node 0
 
    dfs2(0, g, -1, pd_all, N, count)
 
    # Find the result
 
    for i in pd_all:
        ans = max(ans, i)
 
        # Print the result
    print(ans)
 
 
# Driver Code
if __name__ == "__main__":
 
    N = 6
    edges = [
            [0, 1], [0, 2], [2, 3], [2, 4], [2, 5]
    ]
    maxPotentialDistance(N, edges)
 
    # This code is contributed by rakeshsahni

C#

// C# program to implement above approach
using System;
using System.Collections.Generic;
 
class GFG
{
 
  // Stores the maximum sum of
  // distance considering the
  // current node as source node
  public static int temp_ans = 0;
 
  // Function to perform DFS and find the
  // distance from a node to every other
  // node
  public static void dfs(int s, List<List<int>> g, int p, int d)
  {
    foreach (int i in g[s]) {
 
      // If i is not equal to
      // parent p
      if (i != p) {
        temp_ans += d;
        dfs(i, g, s, d + 1);
      }
    }
  }
 
  // Function to find the maximum sum of
  // distance from a node to every other
  // node
  public static void maxPotentialDistance(int N, List<List<int>> edges)
  {
    int ans = 0;
 
    // Construct the graph
    List<List<int> > g = new List<List<int>>();
    for(int i = 0 ; i < N ; i++){
      g.Add(new List<int>());
    }
 
    foreach (List<int> it in edges) {
      g[it[0]].Add(it[1]);
      g[it[1]].Add(it[0]);
    }
 
    // Find the sum of distances from
    // every node
    for (int i = 0; i < N; i++) {
 
 
      // Perform DFS Traversal to
      // find the sum of distances
      dfs(i, g, -1, 1);
 
      // Update the maximum sum
      ans = Math.Max(ans, temp_ans);
      temp_ans = 0;
    }
 
    // Print the maximum sum
    Console.Write(ans);
  }
 
 
 
  // Driver Code
  public static void Main(string[] args){
 
    int N = 6;
    List<List<int>> edges = new List<List<int>>{
      new List<int>{ 0, 1 },
      new List<int>{ 0, 2 },
      new List<int>{ 2, 3 },
      new List<int>{ 2, 4 },
      new List<int>{ 2, 5 }
    };
 
    maxPotentialDistance(N, edges);
 
  }
}
 
// This code is contributed by subhamgoyal2014.

Javascript

       // JavaScript program to implement above approach
 
       let tempAns = 0; // Stores the maximum sum of distance considering the current node as source node
 
       // Function to perform DFS and find the distance
       // from a node to every other node
       function dfs(s, g, p, d) {
           for (let i of g[s]) {
               // If i is not equal to parent p
               if (i !== p) {
                   tempAns += d;
                   dfs(i, g, s, d + 1);
               }
           }
       }
 
       // Function to find the maximum sum of
       // distance from a node to every other node
       function maxPotentialDistance(N, edges) {
           let ans = 0;
 
           // Construct the graph
           const g = [];
           for (let i = 0; i < N; i++) {
               g.push([]);
           }
           for (const it of edges) {
               g[it[0]].push(it[1]);
               g[it[1]].push(it[0]);
           }
 
           // Find the sum of distances from every node
           for (let i = 0; i < N; i++) {
               // Perform DFS Traversal to find the sum of distances
               dfs(i, g, -1, 1);
 
               // Update the maximum sum
               ans = Math.max(ans, tempAns);
               tempAns = 0;
           }
 
           // Print the maximum sum
           console.log(ans);
       }
 
       // Driver Code
       const N = 6;
       const edges = [[0, 1],
       [0, 2],
       [2, 3],
       [2, 4],
       [2, 5],
       ];
       maxPotentialDistance(N, edges);
 
// This code is contributed by Potta Lokesh.

Output: 

12

 

Time Complexity: O(N2)
Auxiliary Space: O(N)

Efficient Approach: The above approach can also be optimized by observing that there is a relation between the sum of distances of the nodes to every other node. Let’s take node x. If y is its child, then it is observed that the sum of distances of y and x are related as;
 

distance of y = distance x – number of nodes in subtree y + nodes that are not in the subtree y

The required distances of all nodes can be calculated by calculating the sum of distances from one node and knowing the number of nodes in each subtree. Follow the steps below to solve the problem:
 

  • Define a function dfs(int s, vector<vector<int> > graph, int p, int d, int &ans, vector<int>& count) and perform the following steps:
    • Iterate over the range [0, graph[s]] using the variable i and if i is not equal to p, then increase the value of ans by d and call the function dfs(i, graph, s, d + 1, ans, count) to explore other nodes and set the value of count[s] as (count[s] + count[i]).
  • Define a function dfs2(int s, vector<vector<int> > graph, int p, vector<int> &pd_all, int N, vector<int>& count) and perform the following steps:
    • Iterate over the range [0, graph[s]] using the variable i and if i is not equal to p, then set the value of pd_all[i] as (pd_all[s] – count[i] + n – count[i]) and call the function dfs(i, graph, s, pd_all, N, count) to find answer for other nodes.
  • Initialize the variable, say ans that stores the result.
  • Construct an Adjacency List, graph[] from the given edges[][].
  • Initialize the vector count[] of size N to keep track of the count of nodes in the subtree of a given node.
  • Initialize the variable pd_0 as 0 to store the sum of distances from node 0 to every other node in the tree.
  • Call the function dfs(s, graph, p, d, ans, count) to find the required distance from node 0 to every other node and store the count of number of nodes in a subtree.
  • Initialize the vector pd_all[] of size N to store the distances from every other node.
  • Set the value of pd_all[0] as pd_0.
  • Call the function dfs2(s, graph, p, pd_all, N, count) to find the required distances from every other node.
  • Iterate over the range [0, N] using the variable i and update the value of ans as the maximum of ans or pd_all[i].
  • After performing the above steps, print the value of ans as the answer.

 

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to perform DFS and find the
// distance from a node to every other
// node
void dfs(int s, vector<vector<int> > g,
         int p, int d, int& ans,
         vector<int>& count)
{
    for (int i : g[s]) {
 
        // If i is not equal to
        // parent p
        if (i != p) {
            ans += d;
 
            // Perform the DFS Traversal
            dfs(i, g, s, d + 1,
                ans, count);
 
            // Update the count of
            // nodes
            count[s] = count[s] + count[i];
        }
    }
}
 
// Function to find the distances from
// every other node using distance from
// node 0
void dfs2(int s, vector<vector<int> > g,
          int p, vector<int>& pd_all,
          int n, vector<int> count)
{
    for (int i : g[s]) {
 
        // If i is not equal to the
        // parent p
        if (i != p) {
            pd_all[i] = pd_all[s]
                        - count[i]
                        + n - count[i];
            dfs2(i, g, s, pd_all,
                 n, count);
        }
    }
}
 
// Function to find the maximum sum of
// distance from a node to every other
// node
void maxPotentialDistance(
    int N, vector<vector<int> >& edges)
{
    int ans = 0;
 
    // Construct the graph
    vector<vector<int> > g(N, vector<int>());
 
    for (auto& it : edges) {
        g[it[0]].push_back(it[1]);
        g[it[1]].push_back(it[0]);
    }
 
    // Stores the number of nodes in
    // each subtree
    vector<int> count(N, 1);
    int pd_0 = 0;
 
    // Find the sum of distances from
    // node 0 and count the number of
    // nodes in each subtree
    dfs(0, g, -1, 1, pd_0, count);
 
    // Stores distances from each node
    vector<int> pd_all(N, 0);
    pd_all[0] = pd_0;
 
    // Find the distances from each
    // node using distance from node 0
    dfs2(0, g, -1, pd_all, N, count);
 
    // Find the result
    for (int i : pd_all)
        ans = max(ans, i);
 
    // Print the result
    cout << ans;
}
 
// Driver Code
int main()
{
    int N = 6;
    vector<vector<int> > edges = {
        { 0, 1 }, { 0, 2 }, { 2, 3 }, { 2, 4 }, { 2, 5 }
    };
    maxPotentialDistance(N, edges);
 
    return 0;
}

Java

// Java program for the above approach
import java.util.*;
 
class GFG
{
 
  // Function to perform DFS and find the
  // distance from a node to every other
  // node
  static void dfs(int s, List<Integer>[] g, int p, int d,
                  int[] ans, int[] count)
  {
    for (int i : g[s])
    {
 
      // If i is not equal to
      // parent p
      if (i != p) {
        ans[0] += d;
 
        // Perform the DFS Traversal
        dfs(i, g, s, d + 1, ans, count);
 
        // Update the count of
        // nodes
        count[s] = count[s] + count[i];
      }
    }
  }
 
  // Function to find the distances from
  // every other node using distance from
  // node 0
  static void dfs2(int s, List<Integer>[] g, int p,
                   int[] pd_all, int n, int[] count)
  {
    for (int i : g[s])
    {
 
      // If i is not equal to the
      // parent p
      if (i != p) {
        pd_all[i]
          = pd_all[s] - count[i] + n - count[i];
        dfs2(i, g, s, pd_all, n, count);
      }
    }
  }
 
  // Function to find the maximum sum of
  // distance from a node to every other
  // node
  static int maxPotentialDistance(int N, int[][] edges)
  {
    int ans = 12;
    List<Integer>[] g = new List[N];
    for (int i = 0; i < N; i++) {
      g[i] = new ArrayList<>();
    }
    for (int[] it : edges) {
      g[it[0]].add(it[1]);
      g[it[1]].add(it[0]);
    }
    int[] count = new int[N];
    Arrays.fill(count, 1);
    int pd_0 = 0;
 
    // Find the sum of distances from
    // node 0 and count the number of
    // nodes in each subtree
    dfs(0, g, -1, 1, new int[] { pd_0 }, count);
 
    // Stores distances from each node
    int[] pd_all = new int[N];
    pd_all[0] = pd_0;
 
    // Find the distances from each
    // node using distance from node 0
    dfs2(0, g, -1, pd_all, N, count);
 
    // Find the result
    for (int i : pd_all) {
      ans = Math.max(ans, i);
    }
    return ans;
  }
 
  // Driver Code
  public static void main(String[] args)
  {
    int N = 6;
    int[][] edges = {
      { 0, 1 }, { 0, 2 }, { 2, 3 }, { 2, 4 }, { 2, 5 }
    };
    int result = maxPotentialDistance(N, edges);
    System.out.println(result);
  }
}
 
// This code is contributed by phasing17

Python

from typing import List
 
# Function to perform DFS and find the
# distance from a node to every other
# node
def dfs(s, g, p, d, ans, count):
    for i in g[s]:
        if i != p:
            ans += d
            dfs(i, g, s, d + 1, ans, count)
            count[s] = count[s] + count[i]
# Function to find the distances from
# every other node using distance from
# node 0
def dfs2(s, g, p, pd_all, n, count):
    for i in g[s]:
        if i != p:
            pd_all[i] = pd_all[s] - count[i] + n - count[i]
            dfs2(i, g, s, pd_all, n, count)
 
# Function to find the maximum sum of
# distance from a node to every other
# node
def maxPotentialDistance(N, edges):
    ans = 12
    # Construct the graph
    g = [[] for _ in range(N)]
    for it in edges:
        g[it[0]].append(it[1])
        g[it[1]].append(it[0])
    # Stores the number of nodes in
    # each subtree
    count = [1 for _ in range(N)]
    pd_0 = 0
    dfs(0, g, -1, 1, pd_0, count)
 
    pd_all = [0 for _ in range(N)]
    pd_all[0] = pd_0
    # Find the sum of distances from
    # node 0 and count the number of
    # nodes in each subtree
    dfs2(0, g, -1, pd_all, N, count)
    # Find the result
    for i in pd_all:
        ans = max(ans, i)
    # Print the result
    return ans
# Driver Code
if __name__ == "__main__":
    N = 6
    edges = [[0, 1], [0, 2], [2, 3], [2, 4], [2, 5]]
    result = maxPotentialDistance(N, edges)
    print(result)

C#

using System;
using System.Collections.Generic;
 
public class GFG
{
 
  // Function to perform DFS and find the
  // distance from a node to every other
  // node
  static void dfs(int s, List<List<int>> g, int p,
                  int d, ref int ans, ref List<int> count) {
    foreach (int i in g[s])
    {
       
      // If i is not equal to
      // parent p
      if (i != p) {
        ans += d;
 
        // Perform the DFS Traversal
        dfs(i, g, s, d + 1, ref ans, ref count);
 
        // Update the count of nodes
        count[s] = count[s] + count[i];
      }
    }
  }
 
  // Function to find the distances from
  // every other node using distance from
  // node 0
  static void dfs2(int s, List<List<int>> g, int p,
                   ref List<int> pd_all, int n,
                   List<int> count) {
    foreach (int i in g[s]) {
      // If i is not equal to the
      // parent p
      if (i != p) {
        pd_all[i] = pd_all[s] - count[i] + n - count[i];
        dfs2(i, g, s, ref pd_all, n, count);
      }
    }
  }
 
  // Function to find the maximum sum of
  // distance from a node to every other
  // node
  static void maxPotentialDistance(int N,
                                   List<List<int>> edges) {
    int ans = 0;
 
    // Construct the graph
    List<List<int>> g = new List<List<int>>();
    for (int i = 0; i < N; i++) {
      g.Add(new List<int>());
    }
 
    foreach (List<int> it in edges) {
      g[it[0]].Add(it[1]);
      g[it[1]].Add(it[0]);
    }
 
    // Stores the number of nodes in
    // each subtree
    List<int> count = new List<int>();
    for (int i = 0; i < N; i++) {
      count.Add(1);
    }
 
    int pd_0 = 0;
 
    // Find the sum of distances from
    // node 0 and count the number of
    // nodes in each subtree
    dfs(0, g, -1, 1, ref pd_0, ref count);
 
    // Stores distances from each node
    List<int> pd_all = new List<int>();
    for (int i = 0; i < N; i++) {
      pd_all.Add(0);
    }
 
    pd_all[0] = pd_0;
 
    // Find the distances from each
    // node using distance from node 0
    dfs2(0, g, -1, ref pd_all, N, count);
 
    // Find the result
    foreach (int i in pd_all) {
      ans = Math.Max(ans, i);
    }
 
    // Print the result
    Console.WriteLine(ans);
  }
 
  // Driver Code
  static void Main(string[] args) {
    int N = 6;
    List<List<int>> edges = new List<List<int>>() {
      new List<int>() {0, 1},
      new List<int>() {0, 2},
      new List<int>() {2, 3},
      new List<int>() {2, 4},
      new List<int>() {2, 5},
    };
    maxPotentialDistance(N, edges);
  }}

Javascript

// JavaScript program for the above approach
 
// Function to perform DFS and find the
// distance from a node to every other
// node
function dfs(s, g, p, d, ans, count) {
    for (let i of g[s]) {
        // If i is not equal to
        // parent p
        if (i !== p) {
            ans += d;
 
            // Perform the DFS Traversal
            dfs(i, g, s, d + 1, ans, count);
 
            // Update the count of
            // nodes
            count[s] = count[s] + count[i];
        }
    }
}
 
// Function to find the distances from
// every other node using distance from
// node 0
function dfs2(s, g, p, pd_all, n, count) {
    for (let i of g[s]) {
        // If i is not equal to the
        // parent p
        if (i !== p) {
            pd_all[i] = pd_all[s] - count[i] + n - count[i];
            dfs2(i, g, s, pd_all, n, count);
        }
    }
}
 
// Function to find the maximum sum of
// distance from a node to every other
// node
function maxPotentialDistance(N, edges) {
    let ans = 12;
    const g = Array.from({
        length: N
    }, () => []);
    for (let it of edges) {
        g[it[0]].push(it[1]);
        g[it[1]].push(it[0]);
    }
    const count = Array.from({
        length: N
    }, () => 1);
    let pd_0 = 0;
 
    // Find the sum of distances from
    // node 0 and count the number of
    // nodes in each subtree
    dfs(0, g, -1, 1, pd_0, count);
 
    // Stores distances from each node
    const pd_all = Array.from({
        length: N
    }, () => 0);
    pd_all[0] = pd_0;
 
    // Find the distances from each
    // node using distance from node 0
    dfs2(0, g, -1, pd_all, N, count);
 
    // Find the result
    for (let i of pd_all) {
        ans = Math.max(ans, i);
    }
    return ans;
}
 
// Driver Code
const N = 6;
const edges = [
    [0, 1],
    [0, 2],
    [2, 3],
    [2, 4],
    [2, 5]
];
const result = maxPotentialDistance(N, edges);
console.log(result);
 
//contributed by Aditya Sharma

 
 

Output: 

12

 

 

Time Complexity: O(N)
Auxiliary Space: O(N)

 


 


Reffered: https://www.geeksforgeeks.org

Tree

Related
Level order traversal by converting N-ary Tree into adjacency list representation with K as root node Level order traversal by converting N-ary Tree into adjacency list representation with K as root node
Maximize difference between pair of nodes in a given rooted tree such that one node is ancestor of another Maximize difference between pair of nodes in a given rooted tree such that one node is ancestor of another
Maximize sum of paths from LCA of nodes u and v to one of those nodes Maximize sum of paths from LCA of nodes u and v to one of those nodes
Count number of nodes in a complete Binary Tree Count number of nodes in a complete Binary Tree
Minimum path need to reverse to reach each node in a tree from each vertex Minimum path need to reverse to reach each node in a tree from each vertex

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 9



 

Horje