Length of intercept cut off from a line by a Circle - Coding

Given six integers, a, b, c, i, j, and k representing the equation of the circle $(x^2 + y^2 + ax + by + c = 0)$ and equation of the line $(ix + jy + k = 0)$ , the task is to find the length of the intercept cut off from the given line to the circle.

Examples:

Input: a = 0, b = 0, c = -4, i = 2, j = -1, k = 1
Output: 3.89872

Input: a = 5, b = 6, c = -16, i = 1, j = 4, k = 3
Output: 6.9282

Approach: The problem can be solved based on the following mathematical fact.

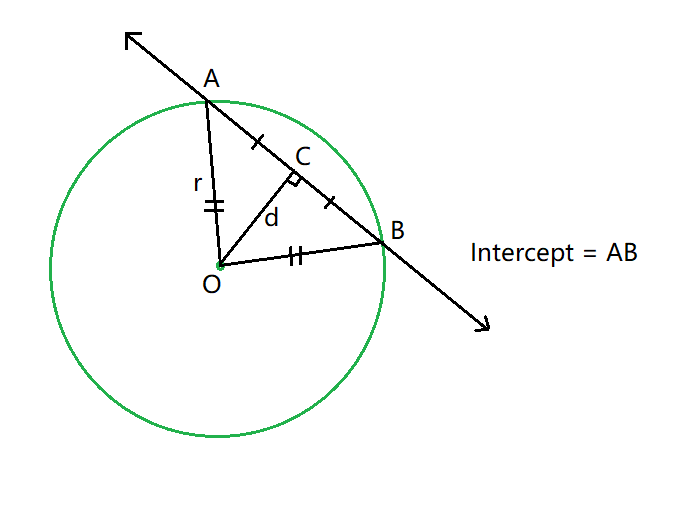
As the line is intercepted by the circle the intercepted segment forms a chord of the circle. Now if a perpendicular is drawn from the centre of the circle to a chord, it divides the chord into two equal parts.

We can easily calculate the radius of the circle and the perpendicular distance of the chord from the centre from the given equations Using them we can get the length of the intercepted line segment.

Follow the steps below to solve the problem:

Find the center of the circle, say $(x_1, y_1)$ as $x_1 = \frac{a}{2}$ and $y_1 = \frac{b}{2}$ .
The perpendicular from the center divides the intercept into two equal parts, therefore calculate the length of one of the parts and multiply it by 2 to get the total length of the intercept.
Calculate the value of radius (r) using the formula: $r = \sqrt(g^2 + f^2 - c)$ , where $g = \frac{a}{2}$ and $f = \frac{b}{2}$
Calculate the value of perpendicular distance ( d ) of center O from the line by using the formula: $d = \frac{|ix_1 + jy_1 + k|} {\sqrt{ i^2 + j^2}}$
Now from the Pythagoras theorem in triangle OCA:
- $OC^2 + AC^2 = OA^2$
- $d^2 + AC^2 = r^2$
- $AC^2 = r^2 - d^2$

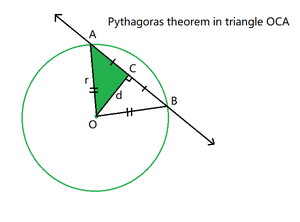
After completing the above steps, print the value of twice of AC to get the length of the total intercept.

Below is the implementation of the above approach.

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the
// radius of a circle
double radius(int a, int b, int c)
{
    // g and f are the coordinates
    // of the center
    int g = a / 2;
    int f = b / 2;
 
    // Case of invalid circle
    if (g * g + f * f - c < 0)
        return (-1);
 
    // Apply the radius formula
    return (sqrt(g * g + f * f - c));
}
 
// Function to find the perpendicular
// distance between circle center and the line
double centerDistanceFromLine(int a, int b, int i, int j,
                              int k)
{
    // Store the coordinates of center
    int g = a / 2;
    int f = b / 2;
 
    // Stores the perpendicular distance
    // between the line and the point
    double distance
        = fabs(i * g + j * f + k) / (sqrt(i * i + j * j));
 
    // Invalid Case
    if (distance < 0)
        return (-1);
 
    // Return the distance
    return distance;
}
 
// Function to find the length of intercept
// cut off from a line by a circle
void interceptLength(int a, int b, int c, int i, int j,
                     int k)
{
    // Calculate the value of radius
    double rad = radius(a, b, c);
 
    // Calculate the perpendicular distance
    // between line and center
    double dist = centerDistanceFromLine(a, b, i, j, k);
 
    // Invalid Case
    if (rad < 0 || dist < 0) {
        cout << "circle not possible";
        return;
    }
 
    // If line do not cut circle
    if (dist > rad) {
        cout << "Line not cutting circle";
    }
 
    // Print the intercept length
    else
        cout << 2 * sqrt(rad * rad - dist * dist);
}
 
// Driver Code
int main()
{
    // Given Input
    int a = 0, b = 0, c = -4;
    int i = 2, j = -1, k = 1;
 
    // Function Call
    interceptLength(a, b, c, i, j, k);
 
    return 0;
}

Java

// Java program for the above approach
class GFG{
 
// Function to find the
// radius of a circle
static double radius(int a, int b, int c)
{
     
    // g and f are the coordinates
    // of the center
    int g = a / 2;
    int f = b / 2;
 
    // Case of invalid circle
    if (g * g + f * f - c < 0)
        return (-1);
 
    // Apply the radius formula
    return (Math.sqrt(g * g + f * f - c));
}
 
// Function to find the perpendicular
// distance between circle center and the line
static double centerDistanceFromLine(int a, int b,
                                     int i, int j,
                                     int k)
{
     
    // Store the coordinates of center
    int g = a / 2;
    int f = b / 2;
 
    // Stores the perpendicular distance
    // between the line and the point
    double distance = Math.abs(i * g + j * f + k) / 
                    (Math.sqrt(i * i + j * j));
 
    // Invalid Case
    if (distance < 0)
        return (-1);
 
    // Return the distance
    return distance;
}
 
// Function to find the length of intercept
// cut off from a line by a circle
static void interceptLength(int a, int b, int c,
                            int i, int j, int k)
{
     
    // Calculate the value of radius
    double rad = radius(a, b, c);
 
    // Calculate the perpendicular distance
    // between line and center
    double dist = centerDistanceFromLine(
        a, b, i, j, k);
 
    // Invalid Case
    if (rad < 0 || dist < 0) 
    {
        System.out.println("circle not possible");
        return;
    }
 
    // If line do not cut circle
    if (dist > rad)
    {
        System.out.println("Line not cutting circle");
    }
 
    // Print the intercept length
    else
        System.out.println(2 * Math.sqrt(
            rad * rad - dist * dist));
}
 
// Driver code
public static void main(String[] args)
{
     
    // Given Input
    int a = 0, b = 0, c = -4;
    int i = 2, j = -1, k = 1;
 
    // Function Call
    interceptLength(a, b, c, i, j, k);
}
}
 
// This code is contributed by abhinavjain194

Python3

# Python3 program for the above approach
import math
 
# Function to find the
# radius of a circle
def radius(a, b, c):
 
    # g and f are the coordinates
    # of the center
    g = a / 2
    f = b / 2
 
    # Case of invalid circle
    if (g * g + f * f - c < 0):
        return(-1)
 
    # Apply the radius formula
    return(math.sqrt(g * g + f * f - c))
 
# Function to find the perpendicular
# distance between circle center and the line
def centerDistanceFromLine(a, b, i, j, k):
 
    # Store the coordinates of center
    g = a / 2
    f = b / 2
 
    # Stores the perpendicular distance
    # between the line and the point
    distance = (abs(i * g + j * f + k) /
         (math.sqrt(i * i + j * j)))
 
    # Invalid Case
    if (distance < 0):
        return (-1)
 
    # Return the distance
    return distance
 
# Function to find the length of intercept
# cut off from a line by a circle
def interceptLength(a, b, c, i, j, k):
 
    # Calculate the value of radius
    rad = radius(a, b, c)
 
    # Calculate the perpendicular distance
    # between line and center
    dist = centerDistanceFromLine(
        a, b, i, j, k)
 
    # Invalid Case
    if (rad < 0 or dist < 0):
        print("circle not possible")
        return
 
    # If line do not cut circle
    if (dist > rad):
        print("Line not cutting circle")
 
    # Print the intercept length
    else:
        print(2 * math.sqrt(
            rad * rad - dist * dist))
 
# Driver Code
if __name__ == "__main__":
 
    # Given Input
    a = 0
    b = 0
    c = -4
    i = 2
    j = -1
    k = 1
 
    # Function Call
    interceptLength(a, b, c, i, j, k)
 
# This code is contributed by ukasp

C#

// C# program for the above approach
using System;
 
class GFG{
     
// Function to find the
// radius of a circle
static double radius(int a, int b, int c)
{
     
    // g and f are the coordinates
    // of the center
    int g = a / 2;
    int f = b / 2;
  
    // Case of invalid circle
    if (g * g + f * f - c < 0)
        return (-1);
  
    // Apply the radius formula
    return(Math.Sqrt(g * g + f * f - c));
}
  
// Function to find the perpendicular
// distance between circle center and the line
static double centerDistanceFromLine(int a, int b,
                                     int i, int j,
                                     int k)
{
     
    // Store the coordinates of center
    int g = a / 2;
    int f = b / 2;
  
    // Stores the perpendicular distance
    // between the line and the point
    double distance = Math.Abs(i * g + j * f + k) /
                    (Math.Sqrt(i * i + j * j));
  
    // Invalid Case
    if (distance < 0)
        return (-1);
  
    // Return the distance
    return distance;
}
  
// Function to find the length of intercept
// cut off from a line by a circle
static void interceptLength(int a, int b, int c,
                            int i, int j, int k)
{
      
    // Calculate the value of radius
    double rad = radius(a, b, c);
  
    // Calculate the perpendicular distance
    // between line and center
    double dist = centerDistanceFromLine(
        a, b, i, j, k);
  
    // Invalid Case
    if (rad < 0 || dist < 0)
    {
        Console.WriteLine("circle not possible");
        return;
    }
  
    // If line do not cut circle
    if (dist > rad)
    {
        Console.WriteLine("Line not cutting circle");
    }
  
    // Print the intercept length
    else
        Console.WriteLine(2 * Math.Sqrt(
            rad * rad - dist * dist));
}
 
// Driver code
public static void Main(String []args)
{
     
    // Given Input
    int a = 0, b = 0, c = -4;
    int i = 2, j = -1, k = 1;
  
    // Function Call
    interceptLength(a, b, c, i, j, k);
}
}
 
// This code is contributed by sanjoy_62

Javascript

<script>
 
        // JavaScript program for the above approach
 
 
        // Function to find the
        // radius of a circle
        function radius(a, b, c) {
 
            // g and f are the coordinates
            // of the center
            let g = a / 2;
            let f = b / 2;
 
            // Case of invalid circle
            if (g * g + f * f - c < 0)
                return (-1);
 
            // Apply the radius formula
            return (Math.sqrt(g * g + f * f - c));
        }
 
        // Function to find the perpendicular
        // distance between circle center and the line
        function centerDistanceFromLine(a, b, i, j, k) {
 
            // Store the coordinates of center
            let g = a / 2;
            let f = b / 2;
 
            // Stores the perpendicular distance
            // between the line and the point
            let distance = Math.abs(i * g + j * f + k) /
                (Math.sqrt(i * i + j * j));
 
            // Invalid Case
            if (distance < 0)
                return (-1);
 
            // Return the distance
            return distance;
        }
 
        // Function to find the length of intercept
        // cut off from a line by a circle
        function interceptLength(a, b, c, i, j, k) {
 
            // Calculate the value of radius
            let rad = radius(a, b, c);
 
            // Calculate the perpendicular distance
            // between line and center
            let dist = centerDistanceFromLine(
                a, b, i, j, k);
 
            // Invalid Case
            if (rad < 0 || dist < 0) {
                document.write("circle not possible");
                return;
            }
 
            // If line do not cut circle
            if (dist > rad) {
                document.write("Line not cutting circle");
            }
 
            // Print the intercept length
            else
                document.write(2 * Math.sqrt(
                    rad * rad - dist * dist));
        }
 
        // Driver code
 
        // Given Input
        let a = 0, b = 0, c = -4;
        let i = 2, j = -1, k = 1;
 
        // Function Call
        interceptLength(a, b, c, i, j, k);
 
        // This code is contributed by Hritik
         
</script>

Output

3.89872

Time Complexity: O(logN), for using in-built sqrt() function.
Auxiliary Space: O(1)

Reffered: https://www.geeksforgeeks.org

Geometric

Related
Determine position of two points with respect to a 3D plane
Check if any pair of semicircles intersect or not
Count number of coordinates from an array satisfying the given conditions
Program to find the Eccentricity of a Hyperbola
Angle between a Pair of Lines

Type:	Geek
Category:	Coding
Sub Category:	Tutorial
Uploaded by:	Admin
Views:	11