.webp)
|
|
Measurement of angles is very important in geometry for solving various geometrical problems and comparing angles in various geometrical figures. We use various geometric tools such as a protractor, and a compass for measuring angles. There are various types of angles measured by us and before learning more about measuring angles we should first learn more about what is an angle. Let’s learn more about Angles, measuring angles, degrees, radians, and others in detail in this article. Table of Content What is an Angle?When two rays are extended together to meet at a point they are formed an angle. Thus, we define the angle as the shape in geometry formed by joining the two rays together. The meeting point of the two rays is called the vertex of the angel and the two rays are called the arm of the angle. The basic structure of an angle is discussed in the image below, .webp)
Types of AnglesOn the basis of the measure of the angles, we divide the angles into seven different categories, that are,
.webp)
What is Measuring Angles?We can measure the angle using various geometrical tools such as a protractor and a compass. Using these tools we can easily find the exact measure of the angles. The protractor is best suited for measuring the various angles exactly as a compass can measure very few angles exactly with lots of difficulties. We can measure the angle in three categories, i.e. in,
DegreesWe define degree as the unit of measuring the angles. A protractor measured the angle in degrees. It is denoted by the ‘°’ symbol. We divide a circle into 360° and thus a semi-circle has 180°. One complete rotation is also called 360°. RadiansWe also measure the angles in radians. It is the SI unit for measuring the angles. It is defined as the ratio of the length of the arc to the radius of the circle at a particular angle. We denote the angle using rad or c and is written as 2 radians or 2 rad or 2c. One complete rotation or 360° equals 2π rad. Thus, we can say that,
We can easily convert Degree to Radian or vice versa using the above formula. Degrees and Radians FormulaAs we know that a circle subtends 2π rad or 360° at its centre. So, 2π radian = 360° π radian = 180° Now, we know that π = 22/7 1 radian = 180°/π = 57°16′(approx) 1° = π /180 = 0.0174(approx) Formulas
Learn more about Degree to Radian. RevolutionThe revolution is the simplest method of measuring the angle. We define one revolution as the complete rotation of the circle. We define revolution such that, One Revolution = 2π Rad = 360° Thus, we can say that half revolution is π Rad or 180° and so on. The below table shows the relationship between degree, radian, and revolution:
How to Measure Angles Using a Protractor?We can easily measure the angle using the protractor. A protractor is a geometrical tool made in the shape of a semi-circle and contains marking from 0° to 180°. It contains the same marking from left to right and right to left. We can use a protractor to measure any angle between 0° to 360°. Now we can easily measure the ∠PQR by following the steps discussed below, 
Steps for Measuring the AngleStep 1: Place the protractor above the line QR such that the midpoint of the protractor coincide with point Q on QR. Step 2: Place the protractor in such a manner that the edge of the protractor is parallel to the line QR. .webp)
Step 3: As we know that the protractor has two marking from left to right and right to left, use the marking from right to left such that we start or count from QR and then measure it to PQ. Now we measure the ∠PQR by seeing the reading between the line PQ and QR. .webp)
Measuring Angle Greater than 180 DegreesAny angle greater than 180 degrees can be easily measured using the protractor by just placing the protractor upside down and then measuring the angle normally as we measure the normal angles. Suppose we have to measure an angle whose value is 275 degrees, we put the protractor upside down such that the vertex of the angle coincides with the midpoint of the protractor and the edge of the protractor is parallel to the arm of the angle. Now we measure the value of the angle normally by following the steps discussed above. Properties of AnglesVarious properties which are highly used in measuring the angles are,
Read More, Measuring Angles ExamplesExample 1: Measure the angle ∠ABC using the protractor. 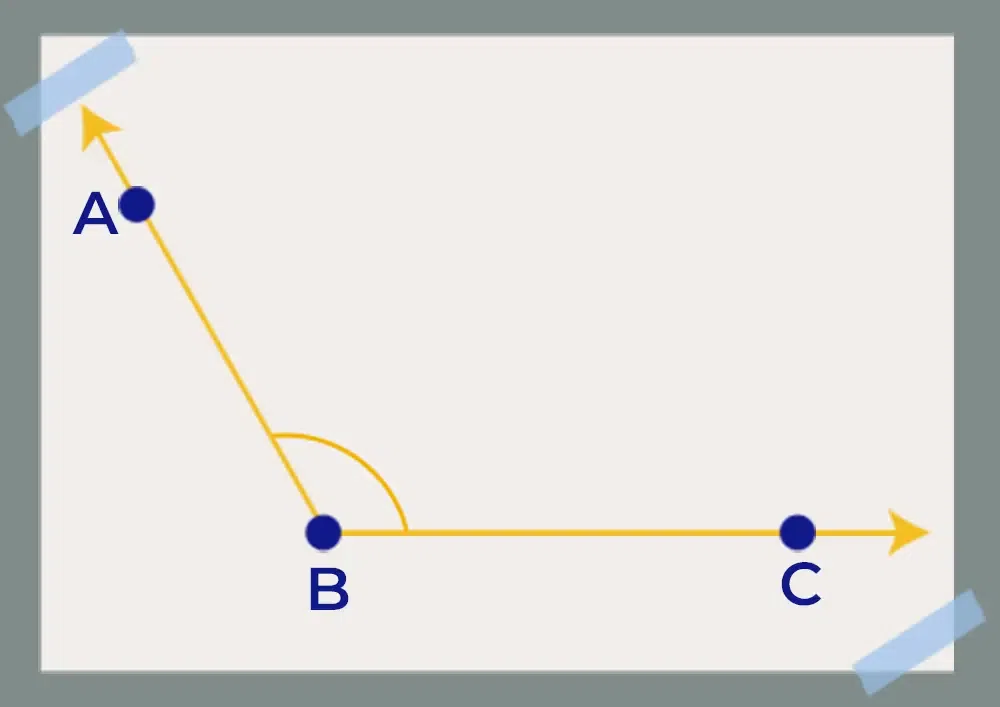
Solution: We can easily measure the angle using the protector as shown in the image below, .webp)
Example 2: In triangle ABC, use the protractor and measure ∠CAB. .webp)
Solution: The measure of the angle ∠CAB of triangle ABC is found using the protector. .webp)
Example 3: Convert 90 degrees to radians. Solution:
Example 4: Convert π/6 rad into degrees. Solution:
FAQs on Measuring AnglesWhat is meant by Measuring Angles?
How should we measure the angles accurately?
What are the 3 Ways of Measurement of Angles?
What are the types of angles which we measure?
Which instrument is used for the Measurement of Angles?
What are the Units for Measuring Angles?
What is the relation between degree and radian?
|
Reffered: https://www.geeksforgeeks.org
| Class 11 |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 8 |