Horje
Implementation of Grey Wolf Optimization (GWO) Algorithm

Previous article Grey wolf optimization- Introduction talked about inspiration of grey wolf optimization, and its mathematical modelling and algorithm. In this article we will implement grey wolf optimization (GWO) for two fitness functions – Rastrigin function and Sphere function. The aim of Grey wolf optimization algorithm is to find minimize of fitness function.

Fitness Functions: 

1) Rastrigin function: Rastrigin function is a non-convex function used as a performance test problem for optimization algorithms.

Function equation:

 

[Tex]f(x_1 \cdots x_n) = 10n + \sum_{i=1}^n (x_i^2 -10cos(2\pi x_i)) [/Tex]


 

[Tex]\text{minimum at }f(0, \cdots, 0) = 0 [/Tex]


 

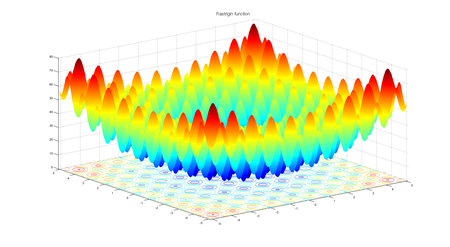
Figure 1 Rastrigin function of 2 variables


 

Rastrigin Function is one of the most challenging functions for an optimization problem. Having a lot of cosine oscillations on the plane introduces a myriad of local minimums in which particles can get stuck.


 

2) Sphere function: Sphere function is used as a performance test problem for optimization algorithms.


 

Function equation:  


 

[Tex]f(x_1 \cdots x_n) = \sum_{i=1}^n x_i^2 [/Tex]


 

[Tex]\text{minimum at }f(0, \cdots, 0) = 0 [/Tex]


 

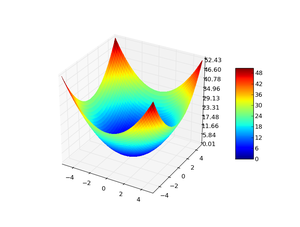Figure2: Sphere function of two variables

 

Choice of hyper-parameters

  • Parameters of problem:
    • Number of dimensions (d) = 3
    • Lower bound (minx) = -10.0
    • Upper bound (maxx) = 10.0
  • Hyperparameters of the algorithm:  
    • Number of grey wolves (N) = 50
    • Maximum number of iterations (max_iter) = 100
  • Inputs: 
    • Fitness function
    • Problem parameters ( mentioned above)
    • Population size (N) and Maximum number of iterations  (max_iter)
    • Algorithm Specific hyperparameters ( None in grey wolf algorithm)

Pseudocode: 

Step1: Randomly initialize Grey wolf population of N particles Xi ( i=1, 2, …, n) Step2: Calculate the fitness value of each individuals sort grey wolf population based on fitness values alpha_wolf = wolf with least fitness value beta_wolf = wolf with second least fitness value gamma_wolf = wolf with third least fitness value Step 3: For Iter in range(max_iter): # loop max_iter times calculate the value of a a = 2*(1 - Iter/max_iter) For i in range(N): # for each wolf a. Compute the value of A1, A2, A3 and C1, C2, C3 A1 = a*(2*r1 -1), A2 = a*(2*r2 -1), A3 = a*(2*r3 -1) C1 = 2*r1, C2 = 2*r2, C3 = 2*r3 b. Computer X1, X2, X3 X1 = alpha_wolf.position - A1*abs(C1*alpha_wolf_position - ith_wolf.position) X2 = beta_wolf.position - A2*abs(C2*beta_wolf_position - ith_wolf.position) X3 = gamma_wolf.position - A3*abs(C3*gamma_wolf_position - ith_wolf.position) c. Compute new solution and it's fitness Xnew = (X1 + X2 + X3) / 3 fnew = fitness( Xnew) d. Update the ith_wolf greedily if( fnew < ith_wolf.fitness) ith_wolf.position = Xnew ith_wolf.fitness = fnew End-for # compute new alpha, beta and gamma sort grey wolf population based on fitness values alpha_wolf = wolf with least fitness value beta_wolf = wolf with second least fitness value gamma_wolf = wolf with third least fitness value End -for Step 4: Return best wolf in the population

Implementation: 


 

Python3

# python implementation of Grey wolf optimization (GWO)
# minimizing rastrigin and sphere function
  
  
import random
import math    # cos() for Rastrigin
import copy    # array-copying convenience
import sys     # max float
  
  
#-------fitness functions---------
  
# rastrigin function
def fitness_rastrigin(position):
  fitness_value = 0.0
  for i in range(len(position)):
    xi = position[i]
    fitness_value += (xi * xi) - (10 * math.cos(2 * math.pi * xi)) + 10
  return fitness_value
  
#sphere function
def fitness_sphere(position):
    fitness_value = 0.0
    for i in range(len(position)):
        xi = position[i]
        fitness_value += (xi*xi);
    return fitness_value;
#-------------------------
  
  
# wolf class 
class wolf:
  def __init__(self, fitness, dim, minx, maxx, seed):
    self.rnd = random.Random(seed)
    self.position = [0.0 for i in range(dim)]
  
    for i in range(dim):
      self.position[i] = ((maxx - minx) * self.rnd.random() + minx)
  
    self.fitness = fitness(self.position) # curr fitness
  
  
  
# grey wolf optimization (GWO)
def gwo(fitness, max_iter, n, dim, minx, maxx):
    rnd = random.Random(0)
  
    # create n random wolves 
    population = [ wolf(fitness, dim, minx, maxx, i) for i in range(n)]
  
    # On the basis of fitness values of wolves 
    # sort the population in asc order
    population = sorted(population, key = lambda temp: temp.fitness)
  
    # best 3 solutions will be called as 
    # alpha, beta and gaama
    alpha_wolf, beta_wolf, gamma_wolf = copy.copy(population[: 3])
  
  
    # main loop of gwo
    Iter = 0
    while Iter < max_iter:
  
        # after every 10 iterations 
        # print iteration number and best fitness value so far
        if Iter % 10 == 0 and Iter > 1:
            print("Iter = " + str(Iter) + " best fitness = %.3f" % alpha_wolf.fitness)
  
        # linearly decreased from 2 to 0
        a = 2*(1 - Iter/max_iter)
  
        # updating each population member with the help of best three members 
        for i in range(n):
            A1, A2, A3 = a * (2 * rnd.random() - 1), a * (
              2 * rnd.random() - 1), a * (2 * rnd.random() - 1)
            C1, C2, C3 = 2 * rnd.random(), 2*rnd.random(), 2*rnd.random()
  
            X1 = [0.0 for i in range(dim)]
            X2 = [0.0 for i in range(dim)]
            X3 = [0.0 for i in range(dim)]
            Xnew = [0.0 for i in range(dim)]
            for j in range(dim):
                X1[j] = alpha_wolf.position[j] - A1 * abs(
                  C1 * alpha_wolf.position[j] - population[i].position[j])
                X2[j] = beta_wolf.position[j] - A2 * abs(
                  C2 *  beta_wolf.position[j] - population[i].position[j])
                X3[j] = gamma_wolf.position[j] - A3 * abs(
                  C3 * gamma_wolf.position[j] - population[i].position[j])
                Xnew[j]+= X1[j] + X2[j] + X3[j]
              
            for j in range(dim):
                Xnew[j]/=3.0
              
            # fitness calculation of new solution
            fnew = fitness(Xnew)
  
            # greedy selection
            if fnew < population[i].fitness:
                population[i].position = Xnew
                population[i].fitness = fnew
                  
        # On the basis of fitness values of wolves 
        # sort the population in asc order
        population = sorted(population, key = lambda temp: temp.fitness)
  
        # best 3 solutions will be called as 
        # alpha, beta and gaama
        alpha_wolf, beta_wolf, gamma_wolf = copy.copy(population[: 3])
          
        Iter+= 1
    # end-while
  
    # returning the best solution
    return alpha_wolf.position
            
#----------------------------
  
  
# Driver code for rastrigin function
  
print("\nBegin grey wolf optimization on rastrigin function\n")
dim = 3
fitness = fitness_rastrigin
  
  
print("Goal is to minimize Rastrigin's function in " + str(dim) + " variables")
print("Function has known min = 0.0 at (", end="")
for i in range(dim-1):
  print("0, ", end="")
print("0)")
  
num_particles = 50
max_iter = 100
  
print("Setting num_particles = " + str(num_particles))
print("Setting max_iter    = " + str(max_iter))
print("\nStarting GWO algorithm\n")
  
  
  
best_position = gwo(fitness, max_iter, num_particles, dim, -10.0, 10.0)
  
print("\nGWO completed\n")
print("\nBest solution found:")
print(["%.6f"%best_position[k] for k in range(dim)])
err = fitness(best_position)
print("fitness of best solution = %.6f" % err)
  
print("\nEnd GWO for rastrigin\n")
  
  
print()
print()
  
  
# Driver code for Sphere function 
print("\nBegin grey wolf optimization on sphere function\n")
dim = 3
fitness = fitness_sphere
  
  
print("Goal is to minimize sphere function in " + str(dim) + " variables")
print("Function has known min = 0.0 at (", end="")
for i in range(dim-1):
  print("0, ", end="")
print("0)")
  
num_particles = 50
max_iter = 100
  
print("Setting num_particles = " + str(num_particles))
print("Setting max_iter    = " + str(max_iter))
print("\nStarting GWO algorithm\n")
  
  
  
best_position = gwo(fitness, max_iter, num_particles, dim, -10.0, 10.0)
  
print("\nGWO completed\n")
print("\nBest solution found:")
print(["%.6f"%best_position[k] for k in range(dim)])
err = fitness(best_position)
print("fitness of best solution = %.6f" % err)
  
print("\nEnd GWO for sphere\n")

Output: 

Begin grey wolf optimization on rastrigin function Goal is to minimize Rastrigin's function in 3 variables Function has known min = 0.0 at (0, 0, 0) Setting num_particles = 50 Setting max_iter = 100 Starting GWO algorithm Iter = 10 best fitness = 2.996 Iter = 20 best fitness = 2.749 Iter = 30 best fitness = 0.470 Iter = 40 best fitness = 0.185 Iter = 50 best fitness = 0.005 Iter = 60 best fitness = 0.001 Iter = 70 best fitness = 0.001 Iter = 80 best fitness = 0.001 Iter = 90 best fitness = 0.000 GWO completed Best solution found: ['0.000706', '-0.000746', '-0.000526'] fitness of best solution = 0.000264 End GWO for rastrigin Begin grey wolf optimization on sphere function Goal is to minimize sphere function in 3 variables Function has known min = 0.0 at (0, 0, 0) Setting num_particles = 50 Setting max_iter = 100 Starting GWO algorithm Iter = 10 best fitness = 0.001 Iter = 20 best fitness = 0.001 Iter = 30 best fitness = 0.000 Iter = 40 best fitness = 0.000 Iter = 50 best fitness = 0.000 Iter = 60 best fitness = 0.000 Iter = 70 best fitness = 0.000 Iter = 80 best fitness = 0.000 Iter = 90 best fitness = 0.000 GWO completed Best solution found: ['-0.000064', '0.000879', '-0.000934'] fitness of best solution = 0.000002 End GWO for sphere

References: 


 


Reffered: https://www.geeksforgeeks.org

Machine Learning

Related
Wine Quality Prediction - Machine Learning Wine Quality Prediction - Machine Learning
Implementing the AdaBoost Algorithm From Scratch Implementing the AdaBoost Algorithm From Scratch
Grey wolf optimization - Introduction Grey wolf optimization - Introduction
Weibull Hazard Plot Weibull Hazard Plot
Emotion Detection using Bidirectional LSTM Emotion Detection using Bidirectional LSTM

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 11



 

Horje