Horje
Radian Measure

The radian is a unit of angular measure used in many areas of mathematics. One radian is defined as the angle subtended at the centre of a circle by an arc whose length is equal to the radius of the circle. It is a natural way of measuring angles and is widely used in various branches of mathematics and physics.

Table of Content

Definition of Radian

The angle that an arc with a length equal to the circle’s radius subtends at its centre is called a radian. Stated otherwise, the angle created at the centre is one radian if the length of the arc equals the radius. This relationship can be stated mathematically as follows:

θ = s / r

Where,

  • θ is Angle in Radians
  • s is Arc Length
  • r is Radius of Circle

Conversion Between Degrees and Radians

To convert between degrees and radians, use the following relationships:

Degrees to Radians

The angular measure unit is a degree. 360 degrees is the whole revolution of a circle. In everyday situations like telling time, navigation, and basic geometry, degrees are usually utilized. Radian is additional unit of angular measure. It’s the angle that results from wrapping a circle’s radius around its perimeter. 2π radians make up a complete revolution around a circle. This is because, given a radius of r, the circumference of a circle is equal to 2πr; conversely, if the radius is 1, the circumference is equal to 2π.

Unit-Cicle-Chart-and-Radian

Since 360 degrees equals 2π radians, we may use this to convert degrees to radians.

Consequently, 1 degree is equivalent to 2π/360 = π/180

Degrees to Radians: Radians = Degrees × π/180

Radians to Degrees

Radians to Degrees relationship can be used to convert radians to degrees: 2π radians equals 360 degrees. Consequently, 1 radian equals 360/2π 360 = 180/π degrees.

An angle can be converted from radians to degrees by multiplying its radian value by 180/π​.

​Radians to Degrees: Degrees = Radians × 180/π

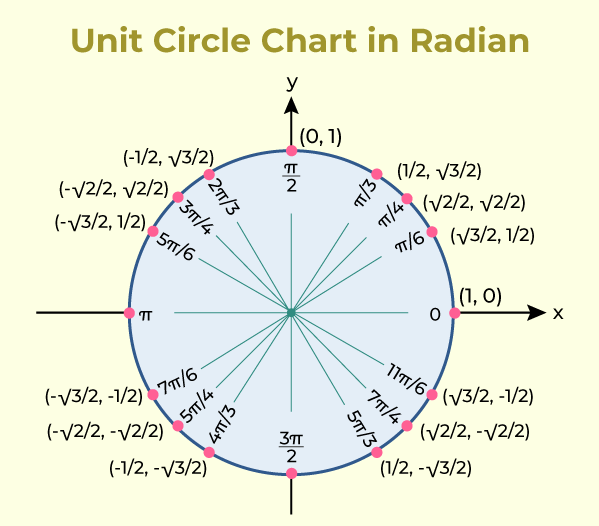
Radian Measure of Common Angles

Although many mathematical applications need the conversion of angles from degrees to radians, this conversion is frequently necessary. Angles like 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, and 360° are quite common. 180o 180ois equal to π radians, which is the connection used to convert between degrees and radians.

Degree-to-Radian

Using the formula:

Radians = Degrees × π / 180

We can determine the radian measure for each common angle using the table added below:

Value of Angle in Radian

Calculation

Value of Angle in Degree

0°

0° × π / 180

= 0 radians

30°

30° × π / 180

= π/6 radians

45°

45° × π / 180

= π/4 radians

60°

60° × π / 180

= π/3 radians

90°

90° × π / 180

= π/2 radians

180°

80° × π / 180

= π radians

360°

360° × π / 180

= 2π radians

Radians in Trigonometric Functions

Angles measured in radians are frequently employed with trigonometric functions like sine, cosine, and tangent. For example, the cosine and sine of an angle measured in radians correspond to the coordinates of points in the unit circle.

Example: Find the sine and cosine of π/2.

Solution:

Using trigonometric table,

  • Sin( π/2) = 1
  • cos( π/2) = 0

Importance of Radian Measure

Since radians are closely related to the characteristics of circles, they offer an intuitive method for measuring angles. They are very helpful in calculus and higher mathematics because of this, as they simplify a lot of formulas and computations.

For example, when angles are measured in radians, the derivatives and integrals of trigonometric functions become considerably easier to understand. Radians are also commonly utilized in computer science, engineering, and physics, which makes them a crucial idea for students studying these subjects.

Applications of Radian Measure

Radian measure is particularly useful in various mathematical contexts, such as:

  • Trigonometry: Radians simplify the differentiation and integration of trigonometric functions.
  • Calculus: Radians are the standard unit for angular measurements in calculus, making it easier to work with derivatives and integrals involving trigonometric functions.
  • Physics: Radians are used in the study of rotational motion, wave mechanics, and other areas of physics where angular measurements are required.
  • Engineering: Many engineering fields use radians for analyzing periodic phenomena, such as electrical engineering and signal processing.

Examples on Radian Measure

Example 1: Convert 90 degrees to radians.

Solution:

Conversion from Degrees to Radians: Radians = Degrees × π/180

Radians = 90° × π/180

= π/2

Example 2: Calculate the radian measure for a 75-degree angle.

Solution:

Conversion from Degrees to Radians: Radians = Degrees × π/180

Radians = 75° × π/180

= 5/12π

Example 3: Convert -90 degrees to radians.

Solution:

Conversion from Degrees to Radians: Radians = Degrees × π/180

Radians = -90° × π/180

= -π/2

Example 4: What is the cosine of π radians?

Solution: 

On the unit circle, cos(π) corresponds to the x-coordinate, which is −1

So, the value of cos(π) is equal to -1

cos(π) = −1

Example 5: What is the angle in degrees if the radian measure is 2π?

Solution:

Conversion from radians to degrees: Degrees = Radians × 180/π

Degrees = 2π × 180/π

= 360 degrees

Example 6: Find the radian measure of an angle subtended by an arc length of 10 units in a circle of radius 5 units.

Solution:

By using formula: θ = s / r

Radians = Arc Length/Radius

= 10/5 = 2

Practice Problems on Radian Measure

Q1. Convert 135 degrees to radians.

Q2. What is the sine of π/2.

Q3. Find the radian measure of a 300-degree angle.

Q4. Determine the radian measure of a 15-degree angle.

Q5. Convert 720 degrees to radians.

Q6. Determine the radian measure of a 30-degree angle.

Q7. Find the radian measure of an angle subtended by an arc length of 20 units in a circle of radius 4 units.

FAQs on Radian Measure

What is the Use of Radians in Trigonometric Functions?

In order to create simpler mathematical relationships, trigonometric functions like sine and cosine are frequently defined and calculated using angles in radians.

How can Radians be Converted to Degrees?

We can convert by multiplying the radian measure by 180/π.

How many Radians does a Complete Circle Measure?

2π radians make up a complete circle.

Are Radians Applied in Actual World?

Yes, radians are commonly employed to measure angles and carry out computations pertaining to circular motion and wave phenomena in physics, engineering, and computer science.

How is Degree Converted to Radian?

In order to find the angle in degrees, multiply it by π/180.


 


Reffered: https://www.geeksforgeeks.org

Mathematics

Related
Class 10 Maths NCERT Solutions in Hindi Class 10 Maths NCERT Solutions in Hindi
How to Teach Cube Roots How to Teach Cube Roots
Addition Table Addition Table
Limits Practice Problems | Solved Problems & Worksheet Limits Practice Problems | Solved Problems & Worksheet
Practice Questions on Polygons Practice Questions on Polygons

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 18



 

Horje