Sampling distribution is essential in various aspects of real life. Sampling distributions are important for inferential statistics. A sampling distribution represents the distribution of a statistic, like the mean or standard deviation, which is calculated from multiple samples of a population. It shows how these statistics vary across different samples drawn from the same population.

In this article, we will discuss the Sampling Distribution in detail and its types along with examples and go through some practice questions too.

What is Sampling Distribution?

Sampling distribution is also known as a finite-sample distribution. Sampling distribution is the probability distribution of a statistic based on random samples of a given population. It represents the distribution of frequencies on how spread apart various outcomes will be for a specific population.

Since population is too large to analyze, you can select a smaller group and repeatedly sample or analyze them. The gathered data, or statistic, is used to calculate the likely occurrence, or probability, of an event.

Important Terminologies in Sampling Distribution

Some important terminologies related to sampling distribution are given below:

• Statistic: A numerical summary of a sample, such as mean, median, standard deviation, etc.

• Parameter: A numerical summary of a population is often estimated using sample statistics.

• Sample: A subset of individuals or observations selected from a population.

• Population: Entire group of individuals or observations that a study aims to describe or draw conclusions about.

• Sampling Distribution: Distribution of a statistic (e.g., mean, standard deviation) across multiple samples taken from the same population.

• Central Limit Theorem(CLT): A fundamental theorem in statistics stating that the sampling distribution of the sample mean tends to be approximately normal as the sample size increases, regardless of the shape of the population distribution.

• Standard Error: Standard deviation of a sampling distribution, representing the variability of sample statistics around the population parameter.

• Bias: Systematic error in estimation or inference, leading to a deviation of the estimated statistic from the true population parameter.

• Confidence Interval: A range of values calculated from sample data that is likely to contain the population parameter with a certain level of confidence.

• Sampling Method: Technique used to select a sample from a population, such as simple random sampling, stratified sampling, cluster sampling, etc.

• Inferential Statistics: Statistical methods and techniques used to draw conclusions or make inferences about a population based on sample data.

• Hypothesis Testing: A statistical method for making decisions or drawing conclusions about a population parameter based on sample data and assumptions about the population.

Understanding Sampling Distribution

Sampling distribution of a statistic is the distribution of all possible values taken by the statistic when all possible samples of a fixed size n are taken from the population. Each random sample that is selected may have a different value assigned to the statistics being studied. Sampling distribution of a statistic is the probability distribution of that statistic.

Factors Influencing Sampling Distribution

A sampling distribution’s variability can be measured either by calculating the standard deviation(also called the standard error of the mean), or by calculating the population variance. The one to be chosen is depending on the context and interferences you want to draw. They both measure the spread of data points in relation to the mean.

3 main factors influencing the variability of a sampling distribution are:

1. Number Observed in a Population: The symbol for this variable is “N.” It is the measure of observed activity in a given group of data.
2. Number Observed in Sample: The symbol for this variable is “n.” It is the measure of observed activity in a random sample of data that is part of the larger grouping.
3. Method of Choosing Sample: How you chose the samples can account for variability in some cases.

Types of Distributions

There are 3 main types of sampling distributions are:

• Sampling Distribution of Mean
• Sampling Distribution of Proportion
• T-Distribution

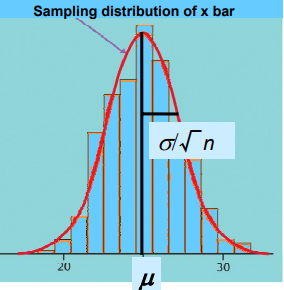
Sampling Distribution of Mean

Mean is the most common type of sampling distribution.

It focuses on calculating the mean or rather the average of every sample group chosen from the population and plotting the data points. The graph shows a normal distribution where the center is the mean of the sampling distribution, which represents the mean of the entire population.

We take many random samples of a given size n from a population with mean µ and standard deviation σ. Some sample means will be above the population mean µ and some will be below, making up the sampling distribution.

For any population with mean µ and standard deviation σ:

• Mean, or center of the sampling distribution of x̄, is equal to the population mean, µ.

= µ

There is no tendency for a sample mean to fall systematically above or below µ, even if the distribution of the raw data is skewed. Thus, the mean of the sampling distribution is an unbiased estimate of the population mean µ.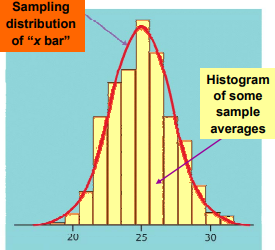

Sampling distribution of the sample mean

• Standard deviation of the sampling distribution is σ/√n, where n is the sample size.

= σ/√n

• Standard deviation of the sampling distribution measures how much the sample statistic varies from sample to sample. It is smaller than the standard deviation of the population by a factor of √n. Averages are less variable than individual observations.
  
  

  sampling distribution of standard deviation

Sampling Distribution of Proportion

Sampling distribution of proportion focuses on proportions in a population. Here, you select samples and calculate their corresponding proportions. The means of the sample proportions from each group represent the proportion of the entire population.

Sampling distribution of proportion – 1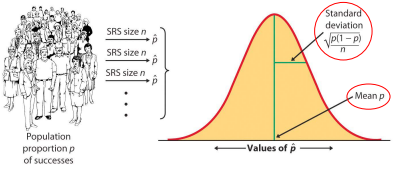

Sampling distribution of proportion – 2

Formula for the sampling distribution of a proportion (often denoted as p̂) is:

p̂ = x/n

where:

• p̂ is Sample Proportion
• x is Number of “successes” or occurrences of Event of Interest in Sample
• n is Sample Size

This formula calculates the proportion of occurrences of a certain event (e.g., success, positive outcome) within a sample.

T-Distribution

Sampling distribution involves a small population or a population about which you don’t know much. It is used to estimate the mean of the population and other statistics such as confidence intervals, statistical differences and linear regression. T-distribution uses a t-score to evaluate data that wouldn’t be appropriate for a normal distribution.

Formula for the t-score, denoted as t, is:

t = [x – μ] / [s /√(n)]

where:

• x is Sample Mean
• μ is Population Mean (or an estimate of it)
• s is Sample Standard Deviation
• n is Sample Size

This formula calculates the difference between the sample mean and the population mean, scaled by the standard error of the sample mean. The t-score helps to assess whether the observed difference between the sample and population means is statistically significant.

Central Limit Theorem[CLT]

Central Limit Theorem is the most important theorem of Statistics.

Central Limit Theorem

According to the central limit theorem, if X₁, X₂, …, X_n is a random sample of size n taken from a population with mean µ and variance σ² then the sampling distribution of the sample mean tends to normal distribution with mean µ and variance σ²/n as sample size tends to large.

This formula indicates that as the sample size increases, the spread of the sample means around the population mean decreases, with the standard deviation of the sample means shrinking proportionally to the square root of the sample size, and the variate Z,

Z = (x – μ)/(σ/√n)

where,

• z is z-score
• x is Value being Standardized (either an individual data point or the sample mean)
• μ is Population Mean
• σ is Population Standard Deviation
• n is Sample Size

This formula quantifies how many standard deviations a data point (or sample mean) is away from the population mean. Positive z-scores indicate values above the mean, while negative z-scores indicate values below the mean. Follows the normal distribution with mean 0 and variance unity, that is, the variate Z follows standard normal distribution.

According to the central limit theorem, the sampling distribution of the sample means tends to normal distribution as sample size tends to large (n > 30).

Examples on Sampling Distribution

Example 1: Mean and standard deviation of the tax value of all vehicles registered in a certain state are μ=$13,525 and σ=$4,180. Suppose random samples of size 100 are drawn from the population of vehicles. What are the mean μ_x̄ and standard deviation σ_x̄ of the sample mean x̄?

Solution:

Since n = 100, the formulas yield

μ_x̄ = μ = $13,525

σ_x̄ = σ / √n = $4180 / √100

σ_x̄ = $418

Example 2: A prototype automotive tire has a design life of 38,500 miles with a standard deviation of 2,500 miles. Five such tires are manufactured and tested. On the assumption that the actual population mean is 38,500 miles and the actual population standard deviation is 2,500 miles, find the probability that the sample mean will be less than 36,000 miles. Assume that the distribution of lifetimes of such tires is normal.

Solution:

Here, we will assume and use units of thousands of miles.

Then sample mean x̄ has

• Mean: μ_x̄ = μ = 38.5
• Standard Deviation: σ_x̄ = σ/√n = 2.5/√5 = 1.11803

Since the population is normally distributed, so is x̄, hence,

P (X < 36) = P(Z < {36 – μ_x̄}/σ_x̄)

P (X < 36) = P(Z < {36 – 38.5}/1.11803)

P (X < 36) = P(Z < -2.24)

P(X < 36) = 0.0125

Therefore, if the tires perform as designed then there is only about a 1.25% chance that the average of a sample of this size would be so low.

Practice Questions on Sample Distribution

Q1: Random samples of size 225 are drawn from a population with mean 100 and standard deviation 20. Find the mean and standard deviation of the sample mean.

Q2: Random samples of size 64 are drawn from a population with mean 32 and standard deviation 5. Find the mean and standard deviation of the sample mean.

Q3: A population has mean 75 and standard deviation 12.

1. Random samples of size 121 are taken. Find the mean and standard deviation of the sample mean.
2. How would the answers to part
3. Change if the size of the samples were 400 instead of 121?

Q4: A population has mean 5.75 and standard deviation 1.02.

1. Random samples of size 81 are taken. Find the mean and standard deviation of the sample mean.
2. How would the answers to part
3. Change if the size of the samples were 25 instead of 81?

Q5: Numerical population of grade point averages at a college has mean 2.61 and standard deviation 0.5. If a random sample of size 100 is taken from the population, what is the probability that the sample mean will be between 2.51 and 2.71?

Q6: Random samples of size 1,600 are drawn from a population in which the proportion with the characteristic of interest is 0.05. Decide whether or not the sample size is large enough to assume that the sample proportion is normally distributed.

Q7: Random samples of size 225 are drawn from a population in which the proportion with the characteristic of interest is 0.25. Decide whether or not the sample size is large enough to assume that the sample proportion is normally distributed.

FAQs on Sampling Distribution

What are the 3 types of sampling distributions?

There are three standard types of sampling distributions in statistics:

• Sampling Distribution of Mean
• Sampling Distribution of Proportion
• T- Distribution

What are the steps for sampling distribution?

Steps for Sampling Distribuition are,

• Step 1: Find Sample Size.

• Step 2: Determine Reference Distribution of Data.

• Step 3: Find Shape of Sampling Distribution.

• Step 4: Find Mean of Sampling Distribution.

• Step 5: Find Standard Deviation of Sampling Distribution.

What are the characteristics of sampling distribution?

Characterstics of Sampling Distributions are:

• Overall shape of distribution is symmetric and approximately normal.
• Center of distribution is very close to true population mean.
• There are no outliers or other important deviations from overall pattern.

What is the difference between a normal distribution and a sampling distribution?

• Normal distribution is a continuous probability distribution with a specific mean and variance.
• Sampling distribution of means is distribution of different means of samples obtained from a population.

What is shape of sampling distribution of sample mean thickness?

1. Skewed to Right
2. Skewed to Left
3. Approximately Normal

Option (3) Approximately Normal is correct

What are factors that influence sampling distribution?

The 3 main factors influencing the variability of a sampling distribution are:

1. Number Observed in a Population
2. Number Observed in Sample
3. Method of Choosing Sample