Horje
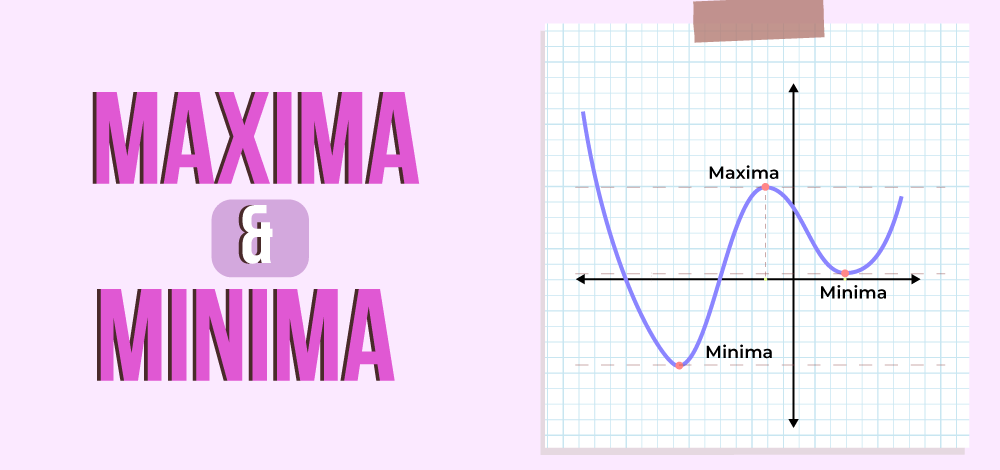
Maxima and Minima: Types, Properties, and Real World Applications

Maxima and Minima in Calculus is an important application of derivatives. The Maxima and Minima of a function are the points that give the maximum and minimum values of the function within the given range. Maxima and minima are called the extremum points of a function.

This article explores the concept of maxima and minima. In addition to details about maxima and minima, we will also cover the types of maxima and minima, properties of Maxima and Minima, provide examples of maxima and minima, and discuss applications of Maxima and Minima.

Maxima-Minima

Table of Content

What are Maxima and Minima of a Function?

The maxima and minima are the most used applications of the derivatives. The maxima and minima provide us with the peaks and valleys of a function. Below we will discuss the maxima and minima of the function in depth and explore the different types of maxima and minima.

Read in Detail: Calculus in Maths

Maxima Definition

Let f(x) be a real function defined on an interval I then, f(x) is said to have the maximum value in I, if there exists a point ‘a’ in I such that f(x) ≤ f(a) for all x ∈ I.

The number f(a) is called the maximum value of f(x) in the interval I and point a is called the point of maxima of f in interval I. The maxima of a function are defined as the point in the given interval where the function value is maximum. In other words, maxima is the highest point on the curve of a function. There are two types of maxima:

  • Local or Relative Maxima
  • Absolute or Global Maxima

Minima Definition

Let f(x) be a real function defined on an interval I then, f(x) is said to have the minimum value in I, if there exists a point ‘a’ in I such that f(x) ≥ f(a) for all x ∈ I.

The number f(a) is called the minimum value of f(x) in interval I and the point a is called the point of minima of f in the interval I. The minima of a function is defined as the point in the given interval where the function value is minimum. In other words, minima is the lowest point on the curve of a function.

There are two types of minima:

  • Relative or Local Minima
  • Absolute or Global Minima

Types of Maxima and Minima

There are two types of maxima and minima. They are listed as follows:

  • Relative or Local Maxima and Minima
  • Absolute or Global Maxima and Minima

Relative Maxima and Minima

The relative maxima or relative minima is the maximum and minimum value which is greater than or lesser than its neighbor.

Relative Maxima

A function f(x) is said to have a relative maximum at x = a if there exists a neighborhood (a – δa, a + δa) of a such that

f(x) < f(a) for all x ∈ (a-δa, a+δa), x ≠ a.

Here, the point a is called the point of relative maxima of a function and f(a) is called as the relative maximum value. The relative maxima is also called as the local maxima of a function.

Relative Minima

A function f(x) is said to have a relative minimum at x = a if there exists a neighborhood (a-δa, a+δa) of a such that

f(x) > f(a) for all x ∈ (a-δa, a+δa), x ≠ a.

Here, the point a is called the point of minima of a function and f(a) is called as the relative minimum value. The relative minima is also called as the local minima of a function. In the article linked below we can learn how to find relative maxima and minima.

Read more about Relative Maxima and Minima.

Absolute Maxima and Absolute Minima

The absolute maxima and the absolute minima is the highest or the lowest value in the entire domain of the function.

Absolute Maxima

A function f(x) with domain D is said to be absolute maximum at x = a where a ∈ D, if f(x) ≤ f(a) for all x ∈ D. The point a is called the point of absolute maxima of function and f(a) is called as the absolute maximum value. The absolute maxima is also called as the global maxima of a function.

Absolute Minima

A function f(x) with domain D is said to be absolute maximum at x = a where a ∈ D , if f(x) ≥ f(a) for all x ∈ D. The point a is called the point of absolute maxima of function and f(a) is called as the absolute maximum value. The absolute maxima is also called as the global maxima of a function.

Read more about Absolute Maxima and Minima.

Absolute vs Relative Maxima and Minima

The difference between absolute and relative maxima and Minima is tabulated below:

Absolute Maxima and Minima

Relative Maxima and Minima
It is also called as global maxima or global minima. It is also called as local maxima or local minima.
It is bounded by domain of the function. It is not bounded by domain of the function.
It is the highest or lowest point of the function. It is the higher or lower among both neighbours.
It is the global peak of the curve. It is the local peak of the curve.

How to Find Maxima and Minima?

We can find maxima and minima of the function by differentiating it. To find the maxima and minima of a function we apply some derivative tests : First Order derivative test and Second Order derivative test. In these tests we differentiate the function and by checking some conditions we get the maxima and minima point of the function.

Some Derivative Tests

To find the maxima and minima we use some derivative tests. The following are the two derivative tests to find maxima and minima.

  • First Order Derivative Test
  • Second Order Derivative Test

First Order Derivative Test

The first order derivative test as the name suggests it uses first order derivative to find maxima and minima. The first order derivative gives the slope of the function.

Let f be a continuous function at critical point c on the open interval l such that f'(c) = 0 then, we will check the nature of the curve. Below are some conditions after checking the nature of the curve, and x increases towards c i.e., the critical point.

  1. If the sign of f'(x) changes from positive to negative, then f(c) is the maximum value and c is the point of local maxima.
  2. If the sign of f'(x) changes from negative to positive, then f(c) is the minimum value and c is the point of local minima.
  3. If the sign of f'(x) neither changes from positive to negative nor from negative to positive, then c is called the point of inflection i.e., neither maxima nor minima.

Read More about First Derivative Test.

Second Derivative Test

The second order derivative test as the name suggests it uses second order derivative to find maxima and minima.

Let f be a function that is two times differentiable at critical point c defined on the open interval l. The following are the conditions:

Condition

Result
If f'(c) = 0 and f”(c) < 0 c is the local maxima and f(c) is the maximum value.
If f'(c) = 0 and f”(c) > 0 c is the local minima and f(c) is the minimum value.
If f”(c) = 0 Test fails.

Properties of Maxima and Minima

Some properties of the maxima and minima are:

  • There is at least one maximum and one minimum that should lie between equal values of f(x), if f(x) is continuous function in its domain.
  • There is one maxima in between two minima and vice-versa. Maxima and minima occur alternatively.
  • There can only be one absolute maxima and one absolute minima over the entire domain.

Solved Examples

Applications of Maxima and Minima

There are many applications of maxima and minima in real-life. Some of these are listed below:

  • Maximizing any about like height, weight etc.
  • Minimizing any quantity like cost etc.

Articles Related to Maxima and Minima

Maxima and Minima Examples

Example 1: Find the local maxima and local minima for the function y = x3 – 3x + 2

Solution:

y = x3 – 3x + 2

Find first order derivative

Differentiating y

y’ = (d / dx) [x3 – 3x + 2]

⇒ y’ = (d / dx) x3 – (d / dx) (3x) + (d / dx) 2

⇒ y’ = 3x2 – 3 + 0

⇒ y’ = 3x2 – 3

Now equate y’ = 0, to find the critical points

y’ = 0

⇒ 3x2 – 3 = 0

⇒ 3x2 = 3

⇒ x2 = 1

⇒ x = 1 or x = -1

The critical points are x = 1 and x = -1

Now we will find second derivative to check the critical point is maxima or minima.

y” = (d / dx) [3x2 – 3]

⇒ y” = (d / dx) [3x2] – (d /dx) [3]

⇒ y” = 6x – 0

⇒ y” = 6x

Now we will put the values of x and find whether y” is greater than 0 or less than 0.

At x = 1

y” = 6(1) = 6

Since, y” > 0 x = 1 is the minima of y

At x = -1

y” = 6(-1) = -6

Since, y” < 0 x = -1 is the maxima of y

The local maxima and minima of y are x = -1 and x = 1 respectively.

Example 2: Find the extremum of the function f(x) = -3x2 + 4x + 7 and the extremum value.

Solution:

y =-3x2 + 4x + 7

Find first order derivative

Differentiating y

y’ = (d / dx) [-3x2 + 4x + 7]

⇒ y’ = (d / dx) (-3x2) – (d / dx) (4x) + (d / dx) 7

⇒ y’ = -6x – 4 + 0

⇒ y’ = -6x – 4

Now equate y’ = 0, to find the critical points

y’ = 0

⇒ -6x – 4 = 0

⇒ -6x = 4

⇒ x = -2 / 3

The critical point is x = -2/3

Now we will find second derivative to check the critical point is maxima or minima.

y” = (d / dx) [-6x – 4]

⇒ y” = (d / dx) [-6x] – (d /dx) [4]

⇒ y” = -6 – 0

⇒ y” = – 6

Since, y” < 0 x = -2 / 3 is the maxima of y and the maximum value is obtained by putting x = -2/3 in y

The local maxima of y is x = -2/3. (extremum)

The maximum value of y = -3(-2/3)2 + 4(-2/3) + 7 = – 2/ 3 – 8 / 3 + 7 = 10 /3 (extremum value)

Example 3: Find the maximum height when a stone is thrown at any time t and height is given by h = -10t2 + 20t + 8.

Solution:

To find the maximum height we will differentiate h = -10t2 + 20t + 8

h’ = (d /dx) [-10t2 + 20t + 8]

⇒ h’ = (d/dx) -10t2 + (d /dx) 20t + (d/ dx) 8

⇒ h’ = -20t + 20 + 0

⇒ h’ = -20t + 20

To find the time at which height is maximum we find h’ = 0

⇒ h’ = 0

⇒ -20t + 20 = 0

⇒ -20t = -20

⇒ t = 1

Now we will find second derivative of h

h” = -20 < 0

Therefore, height is maximum at t = 1

putting value of t in h = -10t2 + 20t + 8

h = -10(1)2 + 20(1) + 8

⇒ h = -10 + 20 + 8

⇒ h = 18

The maximum height is 18 unit.

Example 4: Find the value of the function (x – 1)(x – 2)2 at its minima.

Solution:

Let y = (x – 1)(x – 2)2

⇒ y = (x – 1) (x2 + 4 – 4x)

⇒ y = x3 + 4x – 4x2 – x2 – 4 + 4x

⇒ y = x3 – 5x2 + 8x – 4

Differentiating y

y’ = (d /dx) [x3 – 5x2 + 8x – 4]

⇒ y’ = 3x2 – 10x + 8

Now we will equate y’ = 0 to find the critical points

y’ = 0

3x2 – 10x + 8 = 0

⇒ 3x2 – 6x – 4x + 8 = 0

⇒ 3x (x – 2) – 4 (x – 2) = 0

⇒ (x – 2)(3x – 4) = 0

⇒ x = 2 or x = 4/3

We will find second derivative to check point is maxima or minima

y” = (d / dx) [3x2 – 10x + 8]

⇒ y” = 6x – 10

putting x = 2, y” = 12 – 10 = 2 > 0

So, x = 2 is minima point

putting x = 4 / 3, y” = 8 – 10 = -2 < 0

So, x = 4/3 is maxima point

In the question we have to find minima and value of y at its minima

At x = 2

⇒ y = (x – 1)(x – 2)2

⇒ y = (2 – 1)(2 – 2)2

⇒ y = 1

The value of y at its minima is 1.

Example 5: Find the minimum value of the function 6e3x + 4e-3x

Solution:

Let y = 6e3x + 4e-3x

Find first order derivative

Differentiating y

y’ = (d / dx) [6e3x + 4e-3x]

⇒ y’ = (d / dx) 6e3x + (d / dx) 4e-3x

⇒ y’ = 18e3x – 12e-3x

Now equate y’ = 0, to find the critical points

y’ = 0

⇒ 18e3x – 12e-3x = 0

⇒ 6[3e3x – 2e-3x] = 0

⇒ 3e3x – 2e-3x = 0

⇒ 3e3x = 2e-3x

⇒ e6x = 2/3

vx = log(2/3)1/6

The critical points are x = log(2/3)1/6

Now we will find second derivative to check the critical point is maxima or minima.

y” = (d / dx) [18e3x – 12e-3x]

⇒ y” = 54 e3x + 36 e-3x

Now we will put the values of x and find whether y” is greater than 0 or less than 0.

At x = log(2/3)1/6

Since, y” > 0 x = log(2/3)1/6 is the minima of y

The minima of y is x = log(2/3)1/6

The minimum value of y is at x = log(2/3)1/6

Putting value of x in y

⇒ y = 6e3x + 4e-3x

⇒ y = 6e3log(2/3)1/6 + 4e-3log(2/3)1/6

⇒ y = 6e(1/2)log(2/3) + 4e(-1/2)log(2/3)

⇒ y = 6e(1/2)elog(2/3) + 4e(-1/2)elog(2/3)

⇒ y = (2/3) 6e(1/2) + (2/3) 4e(-1/2)

⇒ y = 4e(1/2) + (8/3)e(-1/2)

Practise Problems on Maxima and Minima

1. Find the maximum and minimum values of the function f(x) = 2x3 – 3x2 – 12x + 1 on the interval [-2, 3].

2. Determine the critical points of the function g(x) = x4 – 4x3 + 6x2 and classify them as local maxima, local minima, or saddle points.

3. Consider the function h(x) = ex – 4x2. Find all the critical points and determine whether they correspond to local maxima, local minima, or neither.

4. A rectangular piece of cardboard measuring 8 inches by 12 inches has squares cut out of its corners, and the sides are folded up to form an open box. Find the dimensions of the squares that should be cut out to maximize the volume of the box.

5. Given the function j(x) = x3 – 12x2 + 36x + 1, find the intervals where the function is increasing and decreasing.

6. Find the dimensions of a rectangular box with a square base and a surface area of 64 square inches that has the maximum possible volume.

7. Determine the critical points of f(x) = x³ – 9x² + 24x – 7 and classify them as local maxima, local minima, or neither.

8. A farmer wants to fence a rectangular area and then divide it into two equal parts with a fence parallel to one of the sides. If the farmer has 1000 feet of fencing, what dimensions will maximize the total area enclosed?

9. Find the points on the curve y = x³ – 3x that are closest to the point (0, 2).

10. A cylindrical can is to be made to hold 1 liter of liquid. Determine the dimensions that will minimize the amount of material used to construct the can.

11. Find the maximum and minimum values of f(x) = 2sin(x) + cos(x) on the interval [0, 2π].

Summary

Optimization problems in calculus involve finding the maximum or minimum values of functions, often within specific constraints or intervals. These problems typically utilize techniques such as finding critical points by setting the first derivative to zero, analyzing the behavior of the function using the first and second derivatives, and applying the closed interval method for bounded intervals. Key concepts include locating local and global extrema, identifying inflection points, and classifying critical points as maxima, minima, or saddle points. Applications range from pure mathematical functions to real-world scenarios in economics, engineering, and physics. Common problem types include optimizing areas, volumes, distances, and profits. The process generally involves formulating an objective function, identifying constraints, finding critical points, and evaluating these points to determine the optimal solution. Understanding these techniques is crucial for solving a wide variety of practical and theoretical problems in calculus and its applications.

Maxima and Minima – FAQs

What is Maxima and Minima of a Function?

The maximum value of a function at any point is called as maxima of a function and the minimum value of a function at any point is called as minima of a function.

What is Point of Inflection?

The stationary point where second order derivative is equal to zero is called as the point of inflection.

How to find the Maxima and Minima of a Function?

To find the maxima and minima of a function, we use the first order derivative test and second order derivative test.

What are Types of Maxima and Minima?

The two types of maxima and minima are:

  • Relative or Local Maxima and Minima
  • Absolute or Global Maxima and Minima

Can there be more than one absolute maxima and absolute minima of a function?

No, there can be only one absolute maxima and absolute minima of a function.
 

What are the Topics Covered in Maxima and Minima Class 12?

In class 12, we lean about following topic related to Maxima and Minima:


 


Reffered: https://www.geeksforgeeks.org

Class 12

Related
Derivative Formulas: List Differentiation Formulas with Examples Derivative Formulas: List Differentiation Formulas with Examples
Orthogonal Matrix: Definition, Properties, and Examples Orthogonal Matrix: Definition, Properties, and Examples
Integration in Math: Definition, Formulas, Types, Examples Integration in Math: Definition, Formulas, Types, Examples
How to find Local Maxima and Minima: Explained with Examples How to find Local Maxima and Minima: Explained with Examples
Second Derivative Test For Maxima and Minima Second Derivative Test For Maxima and Minima

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 16



 

Horje