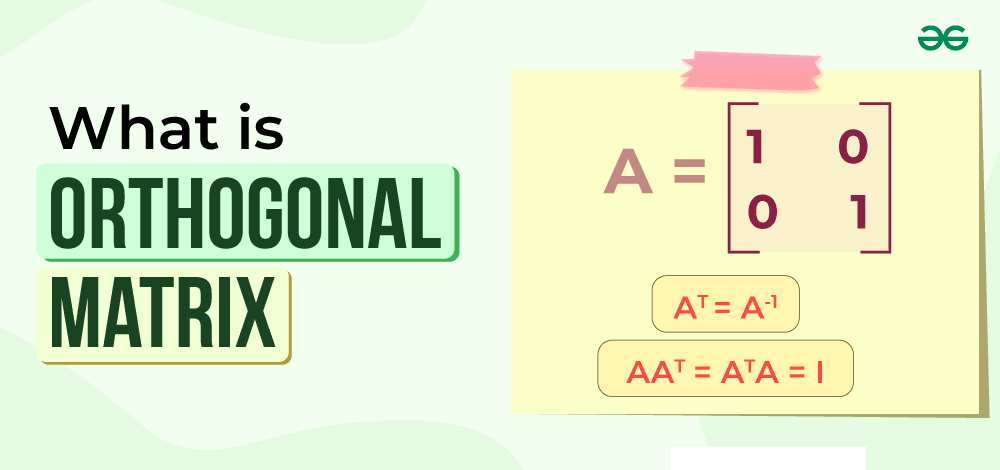
A Matrix is an Orthogonal Matrix when the product of a matrix and its transpose gives an identity value. An orthogonal matrix is a square matrix where transpose of Square Matrix is also the inverse of Square Matrix.

Orthogonal Matrix in Linear Algebra is a type of matrices in which the transpose of matrix is equal to the inverse of that matrix. As we know, the transpose of a matrix is obtained by swapping its row elements with its column elements. For an orthogonal matrix, the product of the transpose and the matrix itself is the identity matrix, as the transpose also serves as the inverse of the matrix.

Let’s know more about Orthogonal Matrix in detail below.

Orthogonal Matrix

Orthogonal Matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1.

Orthogonal Matrix Definition

A Matrix is called Orthogonal Matrix when the transpose of Matrix is inverse of that matrix or the product of Matrix and it’s transpose is equal to an Identity Matrix.

Mathematically, an n x n matrix A is considered orthogonal if

A^T = A^-1

OR

AA^T = A^TA = I

Where,

• A^T is the transpose of the square matrix,
• A^-1 is the inverse of the square matrix, and
• I is the identity matrix of same order as A.

A^T = A^-1 (Condition for an Orthogonal matrix)…(i)

Pre-multiply by A on both sides,

We get, AA^T = AA^-1,

We know this relation of the identity matrix, AA^-1 = I, (of the same order as A).

So we can also write it as AA^T = I. (From (i))

Similarly, we can derive the relation A^TA = I.

So, from the above two equations, we get AA^T = A^TA = I.

Condition for Orthogonal Matrix

For any matrix to be an orthogonal Matrix, it needs to fulfil the following conditions:

• Every two rows and two columns have a dot product of zero, and
• Every row and every column has a magnitude of one.

Orthogonal Matrix in Linear Algebra

The condition of any two vectors to be orthogonal is when their dot product is zero. Similarly, in the case of an orthogonal matrix, every two rows and every two columns are orthogonal. Also, one more condition is that the length of every row (vector) or column (vector) is 1.

For Example, let’s consider a 3×3 matrix, i.e., 

Here, the dot product between vector 1 and vector 2 i.e. between row 1 and row 2

Row 1 ⋅ Row 2 = (1/3)(-2/3)+(2/3)(2/3)+(-2/3)(1/3) =0

So, Row 1 and Row 2 are Orthogonal.

Also, the Magnitude of Row 1 = ((1/3)²+(2/3)²+(-2/3)²)^0.5 = 1

Similarly, we can check for all other rows.

Thus, this matrix A is an example of Orthogonal Matrix.

Example of Orthogonal Matrix

If the transpose of a square matrix with real numbers or values is equal to the inverse matrix of the matrix, the matrix is said to be orthogonal.

Example of 2×2 Orthogonal Matrix

Let’s consider the an 2×2 i.e., .

Let’s check this using the product of the matrix and its transpose.

Thus, 

⇒ 

⇒ 

Which is an Identity Matrix.

Thus, A is an example of an Orthogonal Matrix of order 2×2.

Example of 3×3 Orthogonal Matrix

Let us consider 3D Rotation Matrix i.e., 3×3 matrix such that A = ,

To check this matrix is an orthogonal matrix, we need to

Verify that each column and row matrix is a unit vector, i.e., vector with unit magnitude, and

Verify that the columns and rows are pairwise orthogonal i.e., the dot product between any two rows and columns is 0.

Let’s check.

From the matrix, we get

Column 1: [1, 0, 0]

Column 2: [0, cos(θ), sin(θ)]

Column 3: [0, -sin(θ), cos(θ)]

Now,

|[1, 0, 0]| = √(1² + 0² + 0²) = 1,

|[0, cos(θ), sin(θ)]| = √(0² + cos²(θ) + sin²(θ)) = 1, and

|[0, -sin(θ), cos(θ)]| = √(0² +  sin²(θ) + cos²(θ)) = 1

Thus, each column is a unit vector.

Column 1 ⋅ Column 2 = [1, 0, 0] ⋅ [0, cos(θ), sin(θ)] = 1*0 + 0*cos(θ) + 0*sin(θ) = 0

Similarly, we can check, other columns as well.

Thus, this satisfies all the conditions for a matrix to be orthogonal.

It follows that the provided matrix is an orthogonal matrix given the characteristics of orthogonal matrices.

Determinant of Orthogonal Matrix

Determinant of any Orthogonal Matrix is either +1 or -1. Here, let’s demonstrate the same. Imagine a matrix A that is orthogonal.

For any orthogonal matrix A, we know

A · A^T = I

Taking determinants on both sides,

det(A · A^T) = det(I)

⇒ det(A) · det(A^T) = 1

As, determinant of identity matrix is 1 and det(A) = det(A^T)

Thus, det(A) · det(A) = 1

⇒ [det(A)]² = 1

⇒ det(A) = ±1

Inverse of Orthogonal Matrix

The inverse of the orthogonal matrix is also orthogonal as inverse is same transpose for orthogonal matrix. As for any matrix to be an orthogonal, inverse of the matrix is equal to its transpose.

For an Orthogonal matrix, we know that

A^-1 = A^T

Also A · A^T = A^T · A = I . . . (i)

Let two matrix A and B and if they are inverse of each other then,

A · B = B · A = I . . . (ii)

From (i) and (ii),

B = A^T which is same as A = A^T

So, we conclude that the transpose of an orthogonal matrix is its inverse only.

Learn more

• Inverse of Matrix

Properties of an Orthogonal Matrix

Some of the properties of Orthogonal Matrix are:

• Inverse and Transpose are equivalent. i.e., A^-1 = A^T.
• An identity matrix is the outcome of A and its transpose. That is, AA^T = A^TA = I.
• In light of the fact that its determinant is never 0, an orthogonal matrix is always non-singular.
• An orthogonal diagonal matrix is one whose members are either 1 or -1.
• A^T is orthogonal as well. A^-1 is also orthogonal because A^-1 = A^T.
• The eigenvalues of A are ±1 and the eigenvectors are orthogonal.
• As I × I = I × I = I, and I^T = I. Thus, I an identity matrix (I) is orthogonal.

How to Identify Orthogonal Matrices?

If the transpose of a square matrix with real numbers or elements equals the inverse matrix, the matrix is said to be orthogonal. Or, we may argue that a square matrix is an orthogonal matrix if the product of the square matrix and its transpose results in an identity matrix.

Suppose A is a square matrix with real elements and of n x n order and A^T is the transpose of A. Then according to the definition, if, A^T = A^-1 is satisfied, then,

A ⋅ A^T = I

Eigen Value of Orthogonal Matrix

The eigenvalues of an orthogonal matrix are always complex numbers with a magnitude of 1. In other words, if A is an orthogonal matrix, then its eigenvalues λ satisfy the equation |λ| = 1. Let’s prove the same as follows:

Let A be an orthogonal matrix, and let λ be an eigenvalue of A. Also, let v be the corresponding eigenvector.

By the definition of eigenvalues and eigenvectors, we have:

Av = λv

Now, take the dot product of both sides of this equation with itself:

(Av) ⋅ (Av) = (λv) ⋅ (λv)

Since A is orthogonal, its columns are orthonormal, which means that A^T (the transpose of A) is also its inverse:

A^T ⋅ A = I

Where I is the identity matrix.

Thus, (v^TA^T) ⋅ Av = (λv)^T ⋅ (λv)

⇒ v^T (A^T A) v = (λv)^T (λv)

⇒ v^T I v = (λv)^T (λv)

⇒ v^T v = (λv)^T (λv)

⇒ |v|² = |λ|² |v|²

Now, divide both sides of the equation by |v|²:

1 = |λ|²

⇒ |λ| = 1

Read more

• Eigenvalues and Eigenvectors

Multiplicative Inverse of Orthogonal Matrices

The orthogonal matrix’s inverse is also orthogonal. It is the result of the intersection of two orthogonal matrices. An orthogonal matrix is one in which the inverse of the matrix equals the transpose of the matrix.

Orthogonal Matrix Applications

Some of the most common applications of Orthogonal Matrix are:

• Used in multivariate time series analysis.
• Used in multi-channel signal processing.
• Used in QR decomposition.

Read More

• Matrices
• Types of Matrices
• Adjoint of Matrix

Solved Examples on Orthogonal Matrix

Example 1: Is every orthogonal matrix symmetric?

Solution:

Every time, the orthogonal matrix is symmetric. Thus, the orthogonal matrix is a property of all identity matrices. An orthogonal matrices will also result from the product of two orthogonal matrices. The orthogonal matrix will likewise have a transpose that is orthogonal.

Example 2: Check whether the matrix X is an orthogonal matrix or not?

Solution:

We know that the orthogonal matrix’s determinant is always ±1.

The determinant of X = cos x · cos x – sin x · (-sin x)

⇒ |X| = cos²x + sin²x = 1

⇒ |X| = 1

Hence, X is an Orthogonal Matrix.

Example 3: Prove orthogonal property that multiplies the matrix by transposing results into an identity matrix if A is the given matrix.

Solution:

Thus, 

⇒ 

Which is an identity matrix.

Thus, A is an Orthogonal Matrix.

Practice Problems on Orthogonal Matrix

Q1: Let A be a square matrix:

Determine whether matrix A is orthogonal.

Q2: Given the matrix A:

Is matrix A orthogonal?

Q3: Let Q be an orthogonal matrix. Prove that the transpose of Q is also its inverse, i.e., Q^T = Q^-1

Q4: Consider the matrix C:

Is matrix C orthogonal?

Orthogonal Matrix – FAQs

What is Orthogonal Matrix

If the inverse of a square matrix ‘A’ equals the transpose, the matrix is said to be orthogonal. i.e., A^-1 = A^T. If AA^T = A^TA = I, where I is the identity matrix, and only if it does so, then a matrix A is said to be orthogonal.

Are all Diagonal and Orthogonal Matrices the Same?

Not all diagonal matrices are orthogonal, though. Only when each of a diagonal matrix’s main diagonal members equals 1 or -1 is it considered to be orthogonal.

Why is Identity Matrix Orthogonal?

An identity matrix is an orthogonal matrix because its inverse equals its transpose, or because the identity matrix itself is equal to the product of the identity matrix and its transpose.

Define Orthogonal Matrix.

An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its inverse.

How can you tell If a Matrix is Orthogonal?

To check for matrix is orthogonal or not, we can simply check if A^T · A = I (the identity matrix). If it holds for any matrix A, then A is orthogonal matrix.

What is the Determinant of Orthogonal Matrix?

An orthogonal matrix has a determinant that is either +1 or -1.

What is an Inverse of Orthogonal Matrix?

An orthogonal matrix is one whose inverse is the same as its transpose. In other words, A^-1 = A^T for any orthogonal matrix A.

Does an Orthogonal Matrix Always Have Non-Singularity?

Since its determinant equals 1, an orthogonal matrix is non-singular in all cases.

What is an Orthogonal Matrix Eigenvalues?

The eigenvalues of orthogonal matrices have unit modulus i.e., | λ | = 1 .

What is an Example of an Orthogonal Matrix?

An example of an orthogonal matrix is the 2×2 matrix:

Where x is any Real Number.

What is the Difference between Orthogonal and Orthonormal Matrix?

An orthogonal matrix has orthogonal (perpendicular) columns or rows, meaning their dot products are zero, but they may not have unit lengths. An orthonormal matrix is orthogonal and additionally has columns with unit lengths as well (magnitude 1).