Horje
Sum of leaf nodes at each horizontal level in a binary tree

Given a Binary Tree, the task is to find the sum of leaf nodes at every level of the given tree.

Examples:

Input:

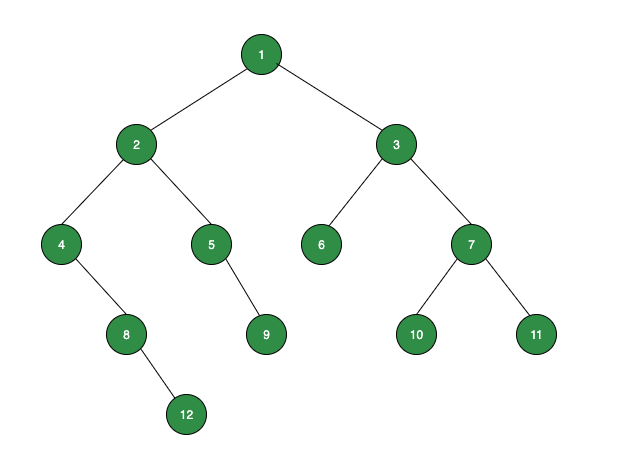
Output:
0
0
6
30
12
Explanation:
Level 1: No leaf node, so sum = 0
Level 2: No leaf node, so sum = 0
Level 3: One leaf node: 6, so sum = 6 
Level 4: Three leaf nodes: 9, 10, 11, so sum = 30
Level 5: One leaf node: 12, so sum = 12

Input:

Output:
0
0
6
28

Approach: The given problem can be solved by using the Level Order Traversal. Follow the steps below to solve the given problem:

  • Create a queue qu, to store the node alongside its level. Also, create a map to store the sum of each level.
  • Perform the level order traversal from the root node and store each node with its level in the queue, and also check the current node for the leaf node. If it’s a leaf node then add its value in the map corresponding to its level.
  • After completing the above steps, print the values in the map as the sum of each level of the given tree.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Tree node structure
class Node {
public:
    int data;
    Node *left, *right;
 
    Node(int data)
    {
        this->data = data;
        left = right = NULL;
    }
};
 
// Function to print the sum of leaf nodes
// at each horizontal level
void printLevelSum(Node* root)
{
    if (root == NULL) {
        cout << "No nodes present\n";
        return;
    }
 
    // Map to hold sum at each level
    map<int, int> mp;
 
    // Queue to hold tree node with level
    queue<pair<Node*, int> > q;
 
    // Root node is at level 1
    q.push({ root, 1 });
 
    pair<Node*, int> p;
 
    // Level Order Traversal of tree
    while (!q.empty()) {
        p = q.front();
        q.pop();
 
        // Create a key for each level
        // in the map
        if (mp.find(p.second) == mp.end()) {
            mp[p.second] = 0;
        }
 
        // If current node is a leaf node
        if (p.first->left == NULL
            && p.first->right == NULL) {
 
            // Adding value in the map
            // corresponding to its level
            mp[p.second] += p.first->data;
        }
 
        if (p.first->left)
            q.push({ p.first->left, p.second + 1 });
        if (p.first->right)
            q.push({ p.first->right, p.second + 1 });
    }
 
    // Print the sum at each level
    for (auto i : mp) {
        cout << i.second << endl;
    }
}
 
// Driver Code
int main()
{
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->left = new Node(6);
    root->right->right = new Node(7);
    root->left->left->right = new Node(8);
    root->left->right->right = new Node(9);
    root->right->right->left = new Node(10);
    root->right->right->right = new Node(11);
    root->left->left->right->right = new Node(12);
 
    printLevelSum(root);
 
    return 0;
}

Java

// Java program for the above approach
 
import java.util.LinkedList;
import java.util.Map;
import java.util.Queue;
import java.util.HashMap;
 
public class Print_Level_Sum_Btree {
     
    /* A tree node structure */
    static class Node {
        int data;
        Node left;
        Node right;
        Node(int data){
            this.data = data;
            left = null;
            right = null;
        }
    }
     
    // User defined class Pair to hold
    // the node and its level
    static class Pair{
        Node n;
        int i;
        Pair(Node n, int i){
            this.n = n;
            this.i = i;
        }
         
    }
     
    // Function to print the sum of leaf nodes
    // at each horizontal level
    static void printLevelSum(Node root)
    {
        if (root == null)
        {
            System.out.println("No nodes present");
            return;
        }
         
        // hashmap to hold sum at each level
        HashMap<Integer, Integer> map = new HashMap<>();
         
         
        // queue to hold tree node with level
        Queue<Pair> q = new LinkedList<Pair>();
     
        // Root node is at level 1
        q.add(new Pair(root, 1));
     
        Pair p;
     
        // Level Order Traversal of tree
        while (!q.isEmpty()) {
            p = q.peek();
            q.remove();
             
              // Create a key for each level
            // in the map
            if (!map.containsKey(p.i))
                map.put(p.i, 0);
             
              // If current node is a leaf node
            if (p.n.left == null && p.n.right == null)
            {
                  // Adding value in the map
                // corresponding to its level
                map.put(p.i, map.get(p.i) + p.n.data);
            }
             
            if (p.n.left != null)
                q.add(new Pair(p.n.left, p.i + 1));
            if (p.n.right != null)
                q.add(new Pair(p.n.right, p.i + 1));
        }
         
          // Print the sum at each level
        for (Map.Entry mapElement : map.entrySet()) {
            int value = ((int)mapElement.getValue());
   
            System.out.println(value);
        }
    }
     
    // Driver Code
    public static void main(String args[])
    {
        Node root = null;
        root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
        root.right.left = new Node(6);
        root.right.right = new Node(7);
        root.left.left.right = new Node(8);
        root.left.right.right = new Node(9);
        root.right.right.left = new Node(10);
        root.right.right.right = new Node(11);
        root.left.left.right.right = new Node(12);
         
        printLevelSum(root);
    }
}
 
// This code is contributed by vineetsharma36.

Python3

# Python3 program for the above approach
class newNode:
   
    # Construct to create a new node
    def __init__(self, key):
        self.data = key
        self.left = None
        self.right = None
 
# Function to print the sum of leaf nodes
# at each horizontal level
def printLevelSum(root):
 
    if (not root):
        print("No nodes present")
        return
 
    # Dictionary to hold sum at each level
    dict = {}
 
    # queue to hold tree node with level
    q = []
 
    # Root node is at level 1
    q.append([root, 1])
 
    p = []
 
    # Level order Traversal of Tree
    while (len(q)):
        p=q[0]
        q.pop(0)
         
        # Create a key for each level
        # in the dictionary
        if (p[1] not in dict.keys()):
            dict[p[1]] = 0
             
        # If current node is a leaf node
        if (not p[0].left and not p[0].right):
            # Adding value in the dictionary
            # corresponding to its level
            dict[p[1]] = p[0].data + dict.get(p[1])
         
        if (p[0].left):
            q.append([p[0].left, p[1] + 1])
        if (p[0].right):
            q.append([p[0].right, p[1] + 1])
     
    # Print the sum at each level
    for sum in dict.values():
        print(sum)
 
# Driver Code
if __name__ == '__main__':
 
    root = newNode(1)
    root.left = newNode(2)
    root.right = newNode(3)
    root.left.left = newNode(4)
    root.left.right = newNode(5)
    root.right.left = newNode(6)
    root.right.right = newNode(7)
    root.left.left.right = newNode(8)
    root.left.right.right = newNode(9)
    root.right.right.left = newNode(10)
    root.right.right.right = newNode(11)
    root.left.left.right.right = newNode(12)
     
    printLevelSum(root)
     
    # This code is contributed by vineetsharma36.

C#

// C# program for the above approach
using System;
using System.Collections.Generic;
 
public class Print_Level_Sum_Btree {
     
    /* A tree node structure */
   public class Node {
      public  int data;
      public  Node left;
      public  Node right;
      public  Node(int data){
            this.data = data;
            left = null;
            right = null;
        }
    }
     
    // User defined class Pair to hold
    // the node and its level
  public  class Pair{
       public Node n;
      public  int i;
      public  Pair(Node n, int i){
            this.n = n;
            this.i = i;
        }
         
    }
     
    // Function to print the sum of leaf nodes
    // at each horizontal level
    static void printLevelSum(Node root)
    {
        if (root == null)
        {
            Console.WriteLine("No nodes present");
            return;
        }
         
        // hashmap to hold sum at each level
        Dictionary<int, int> map = new Dictionary<int,int>();
         
         
        // queue to hold tree node with level
        Queue<Pair> q = new Queue<Pair>();
     
        // Root node is at level 1
        q.Enqueue(new Pair(root, 1));
     
        Pair p;
     
        // Level Order Traversal of tree
        while (q.Count!=0) {
            p = q.Peek();
            q.Dequeue();
             
              // Create a key for each level
            // in the map
            if (!map.ContainsKey(p.i))
                map.Add(p.i, 0);
             
              // If current node is a leaf node
            if (p.n.left == null && p.n.right == null)
            {
                  // Adding value in the map
                // corresponding to its level
                map[p.i]= map[p.i] + p.n.data;
            }
             
            if (p.n.left != null)
                q.Enqueue(new Pair(p.n.left, p.i + 1));
            if (p.n.right != null)
                q.Enqueue(new Pair(p.n.right, p.i + 1));
        }
         
          // Print the sum at each level
       foreach(KeyValuePair<int, int> entry in map){
            int value = (entry.Value);
   
            Console.WriteLine(value);
        }
    }
     
    // Driver Code
    public static void Main(String []args)
    {
        Node root = null;
        root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
        root.right.left = new Node(6);
        root.right.right = new Node(7);
        root.left.left.right = new Node(8);
        root.left.right.right = new Node(9);
        root.right.right.left = new Node(10);
        root.right.right.right = new Node(11);
        root.left.left.right.right = new Node(12);
         
        printLevelSum(root);
    }
}
 
// This code is contributed by umadevi9616

Javascript

<script>
// Javascript program for the above approach
 
// Tree node structure
class Node {
  constructor(data) {
    this.data = data;
    this.left = this.right = null;
  }
}
 
// Function to print the sum of leaf nodes
// at each horizontal level
function printLevelSum(root) {
  if (root == null) {
    document.write("No nodes present\n");
    return;
  }
 
  // Map to hold sum at each level
  let mp = new Map();
 
  // Queue to hold tree node with level
  let q = [];
 
  // Root node is at level 1
  q.push([root, 1]);
 
  let p = [];
 
  // Level Order Traversal of tree
  while (q.length) {
    p = q[q.length - 1];
    q.pop();
 
    // Create a key for each level
    // in the map
    if (!mp.has(p[1])) {
      mp.set(p[1], 0);
    }
 
    // If current node is a leaf node
    if (p[0].left == null && p[0].right == null) {
      // Adding value in the map
      // corresponding to its level
      mp.set(p[1], mp.get(p[1]) + p[0].data);
    }
 
    if (p[0].left) q.push([p[0].left, p[1] + 1]);
    if (p[0].right) q.push([p[0].right, p[1] + 1]);
  }
 
  // Print the sum at each level
  for (let i of mp) {
    document.write(i[1] + "<bR>");
  }
}
 
// Driver Code
 
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.left.left.right = new Node(8);
root.left.right.right = new Node(9);
root.right.right.left = new Node(10);
root.right.right.right = new Node(11);
root.left.left.right.right = new Node(12);
 
printLevelSum(root);
 
</script>

Output

0
0
6
30
12

Time Complexity: O(N)
Auxiliary Space: O(N)

Another Approach(Recursive):
Follow the below steps to solve the problem:
1). In this method we will traverse the each node of binary tree recursively and keep track of level with each node.
2). If the current node is leaf node then we will store the node value in vector otherwise if the node is not leaf node then we will add the sum in 0 so it will not effects out answer.
3). Finally print the array of answers.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include<bits/stdc++.h>
using namespace std;
 
// struct of binary tree node
struct Node{
    int data;
    Node* left;
    Node* right;
    Node(int data){
        this->data = data;
        this->left = NULL;
        this->right = NULL;
    }
};
 
// function to find the height of binary tree
int height(Node* root){
    if(root == NULL) return 0;
    int l = height(root->left);
    int r = height(root->right);
    return max(l,r)+1;
}
 
// Function to print the sum of leaf nodes
// at each horizontal level
void printLevelSum(Node* root, vector<int> &ans, int level){
    if(root == NULL) return;
    if(root->left == NULL && root->right == NULL){
        ans[level] += root->data;
    }else{
        ans[level] += 0;
    }
    printLevelSum(root->left, ans, level+1);
    printLevelSum(root->right, ans, level+1);
}
 
//driver code
int main(){
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->left = new Node(6);
    root->right->right = new Node(7);
    root->left->left->right = new Node(8);
    root->left->right->right = new Node(9);
    root->right->right->left = new Node(10);
    root->right->right->right = new Node(11);
    root->left->left->right->right = new Node(12);
  
    vector<int> ans(height(root), 0);
    printLevelSum(root, ans, 0);
    for(int i : ans)
        cout<<i<<endl;
    return 0;
}
 
// This code is contributed by Yash Agarwal(yashagarwal2852002)

Java

import java.util.*;
 
// Node class for binary tree
class Node {
    int data;
    Node left, right;
  
    public Node(int data) {
        this.data = data;
        left = right = null;
    }
}
  
// Class for the binary tree
class BinaryTree {
    Node root;
  
    // Function to find the height of binary tree
    int height(Node node) {
        if (node == null)
            return 0;
  
        int lheight = height(node.left);
        int rheight = height(node.right);
  
        return Math.max(lheight, rheight) + 1;
    }
  
    // Function to print the sum of leaf nodes
    // at each horizontal level
    void printLevelSum(Node node, int[] ans, int level) {
        if (node == null)
            return;
  
        if (node.left == null && node.right == null) {
            ans[level] += node.data;
        } else {
            ans[level] += 0;
        }
  
        printLevelSum(node.left, ans, level + 1);
        printLevelSum(node.right, ans, level + 1);
    }
  
    // Driver code
    public static void main(String args[]) {
        BinaryTree tree = new BinaryTree();
  
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);
        tree.root.left.left.right = new Node(8);
        tree.root.left.right.right = new Node(9);
        tree.root.right.right.left = new Node(10);
        tree.root.right.right.right = new Node(11);
        tree.root.left.left.right.right = new Node(12);
  
        int[] ans = new int[tree.height(tree.root)];
        tree.printLevelSum(tree.root, ans, 0);
        for (int i : ans) {
            System.out.println(i);
        }
    }
}

Python

# Python program for the above approach
 
# class of binary tree node
class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
 
# function to find the height of binary tree
def height(root):
    if root is None:
        return 0
    l = height(root.left)
    r = height(root.right)
    return max(l, r) + 1
 
# function to print the sum of leaf nodes
# at each horizontal level
def printLevelSum(root, ans, level):
    if root is None:
        return
    if root.left is None and root.right is None:
        ans[level] += root.data
    else:
        ans[level] += 0
    printLevelSum(root.left, ans, level+1)
    printLevelSum(root.right, ans, level+1)
 
# driver code
if __name__ == '__main__':
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    root.right.left = Node(6)
    root.right.right = Node(7)
    root.left.left.right = Node(8)
    root.left.right.right = Node(9)
    root.right.right.left = Node(10)
    root.right.right.right = Node(11)
    root.left.left.right.right = Node(12)
 
    ans = [0] * height(root)
    printLevelSum(root, ans, 0)
    for i in ans:
        print(i)

C#

// C# code
using System;
using System.Collections.Generic;
 
public class Node
{
  public int data;
  public Node left, right;
 
  public Node(int data)
  {
    this.data = data;
    left = right = null;
  }
}
 
public class BinaryTree
{
  public Node root;
 
  // Function to find the height of binary tree
  public int height(Node node)
  {
    if (node == null)
      return 0;
 
    int lheight = height(node.left);
    int rheight = height(node.right);
 
    return Math.Max(lheight, rheight) + 1;
  }
 
  // Function to print the sum of leaf nodes
  // at each horizontal level
  public void printLevelSum(Node node, int[] ans, int level)
  {
    if (node == null)
      return;
 
    if (node.left == null && node.right == null)
    {
      ans[level] += node.data;
    }
    else
    {
      ans[level] += 0;
    }
 
    printLevelSum(node.left, ans, level + 1);
    printLevelSum(node.right, ans, level + 1);
  }
 
  // Driver code
  public static void Main(string[] args)
  {
    BinaryTree tree = new BinaryTree();
 
    tree.root = new Node(1);
    tree.root.left = new Node(2);
    tree.root.right = new Node(3);
    tree.root.left.left = new Node(4);
    tree.root.left.right = new Node(5);
    tree.root.right.left = new Node(6);
    tree.root.right.right = new Node(7);
    tree.root.left.left.right = new Node(8);
    tree.root.left.right.right = new Node(9);
    tree.root.right.right.left = new Node(10);
    tree.root.right.right.right = new Node(11);
    tree.root.left.left.right.right = new Node(12);
 
    int[] ans = new int[tree.height(tree.root)];
    tree.printLevelSum(tree.root, ans, 0);
    foreach (int i in ans)
    {
      Console.WriteLine(i);
    }
  }
}

Javascript

// JavaScript program for the above approach
// structure of binary tree node
class Node{
    constructor(data){
        this.data = data;
        this.left = null;
        this.right = null;
    }
}
 
// function to find the height of binary tree
function height(root){
    if(root == null) return 0;
    let l = height(root.left);
    let r = height(root.right);
    return Math.max(l,r)+1;
}
 
let ans;
// Function to print the sum of leaf nodes
// at each horizontal level
function printLevelSum(root, level){
    if(root == null) return;
    if(root.left == null && root.right == null){
        ans[level] += root.data;
    }else{
        ans[level] += 0;
    }
    printLevelSum(root.left, level+1);
    printLevelSum(root.right, level+1);
}
 
// driver code
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.left.left.right = new Node(8);
root.left.right.right = new Node(9);
root.right.right.left = new Node(10);
root.right.right.right = new Node(11);
root.left.left.right.right = new Node(12);
 
ans = new Array(height(root)).fill(0);
printLevelSum(root, 0);
for(let i = 0; i<ans.length; i++){
    console.log(ans[i]);
}
// THIS CODE IS CONTRIBUTED BY KIRTI AGARWAL(KIRTIAGARWAL23121999)

Output

0
0
6
30
12

Time Complexity: O(N) where N is the number of nodes in given binary tree.
Auxiliary Space: O(h) where h is the height of binary tree due to recursion.


 


Reffered: https://www.geeksforgeeks.org

Tree

Related
Maximum sum of distances of a node to every other node Maximum sum of distances of a node to every other node
Level order traversal by converting N-ary Tree into adjacency list representation with K as root node Level order traversal by converting N-ary Tree into adjacency list representation with K as root node
Maximize difference between pair of nodes in a given rooted tree such that one node is ancestor of another Maximize difference between pair of nodes in a given rooted tree such that one node is ancestor of another
Maximize sum of paths from LCA of nodes u and v to one of those nodes Maximize sum of paths from LCA of nodes u and v to one of those nodes
Count number of nodes in a complete Binary Tree Count number of nodes in a complete Binary Tree

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 13



 

Horje