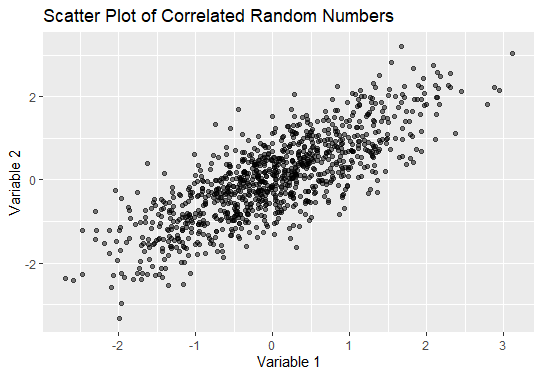
Generating correlated random numbers is a common task in statistical simulations and financial modeling. This article will walk you through the process of generating correlated random numbers in R Programming Language providing a comprehensive explanation and step-by-step examples.

Understanding Correlated Random Numbers

Correlated random numbers are a set of random numbers that exhibit a specific correlation structure. Correlation measures the strength and direction of the relationship between two random variables. In the context of random number generation, you might need correlated random numbers to simulate real-world phenomena where variables are not independent.

For example, in financial modeling, the returns of different stocks often show some degree of correlation. To simulate such scenarios accurately, you need to generate correlated random returns.

Generate Correlated Random Numbers Using the MASS Package

The MASS package in R provides functions to generate multivariate normal distributions, which can be used to create correlated random numbers.

Step 1: Install and Load Necessary Packages

First we will install and load the Necessary Packages.

# Install the MASS package if not already installed
install.packages("MASS")

# Load the MASS package
library(MASS)

Step 2: Define the Mean Vector and Covariance Matrix

To generate correlated random numbers, you need to specify the mean vector and the covariance matrix. The mean vector contains the means of each variable, and the covariance matrix defines the correlation structure.

# Define the mean vector
mean_vector <- c(0, 0)

# Define the covariance matrix
cov_matrix <- matrix(c(1, 0.8, 0.8, 1), nrow = 2)

In this example, we have two variables with means of 0 and a covariance matrix indicating that the variables have a correlation of 0.8.

Step 3: Generate Correlated Random Numbers

Using the mvrnorm function from the MASS package, you can generate correlated random numbers.

# Set the seed for reproducibility
set.seed(123)

# Generate 1000 correlated random numbers
n <- 1000
correlated_data <- mvrnorm(n, mu = mean_vector, Sigma = cov_matrix)

# Convert to a data frame for easier manipulation
correlated_df <- data.frame(correlated_data)
names(correlated_df) <- c("Variable1", "Variable2")

# Print the first few rows
head(correlated_df)

Output:

   Variable1   Variable2
1 -0.2168147 -0.84661309
2  0.1104971 -0.54722820
3  1.4844064  1.47303469
4  0.1086876  0.02509269
5  0.9288261 -0.68351986
6  1.2979953  1.95611173

Step 4: Visualize the Correlation

You can use a scatter plot to visualize the correlation between the two generated variables.

# Load the ggplot2 package for plotting
library(ggplot2)

# Scatter plot of the correlated variables
ggplot(correlated_df, aes(x = Variable1, y = Variable2)) +
  geom_point(alpha = 0.5) +
  labs(title = "Scatter Plot of Correlated Random Numbers",
       x = "Variable 1",
       y = "Variable 2")

Output:

Generate Correlated Random Numbers in R

Conclusion

Generating correlated random numbers in R is straightforward with the help of packages like MASS and mvtnorm. By defining the mean vector and covariance matrix, you can simulate real-world scenarios where variables exhibit correlation. The examples provided in this article demonstrate how to generate and visualize correlated random numbers, offering a solid foundation for further exploration and application in various fields.