|
Injective Functions, also called one-to-one functions are a fundamental concept in mathematics because they establish a unique correspondence between elements of their domain and codomain, ensuring that no two distinct elements in the domain map to the same element in the codomain.
In the world of injective functions, consider two sets, Set A and Set B. The unique characteristic of injective functions is that every element in Set A corresponds to a distinct element in Set B and there is no sharing or repetition. This article provides a well-rounded description of the concept of “Injective Function”, including definitions, examples, properties, and many more.
What is an Injective Function?
An injective function in math is like a special matching game between two sets, Set A and Set B. In this game, every item in Set A is matched with an item in Set B, but there are some rules:
- Each item in Set A can only be matched with one item in Set B, not more than one.
- And no two different items from Set A can be matched to the same item in Set B.
So, when you look at a figure, you’ll see that each item in Set B is connected to only one item (or maybe none) in Set A.
Injective Function Definition
Formally, a function f: A → B is said to be injective if, for all elements a1 and a2 in the domain A, such that
f(a1) = f(a2) implies that a1 = a2
OR
f(a1) ≠ f(a2) implies that a1 ≠ a2
Injective Function Example
Some examples of Injective functions are:
Mapping Diagram for Injective Function
The following illustration shows the mapping diagram for injective function.

Properties of Injective Function
There are various properties of Injecive functions, some of those are listed as follows:
- For every input element in the domain of the function, there is a unique output element in the codomain.
- Injective functions are often monotonic i.e., function is either strictly increases or strictly decreases as you move along the real number line.
- An injective function does not have any critical points (i.e., points where the derivative is zero or undefined) within its domain.
- An injective function that is also surjective (onto) is called a bijective function.
Some more properties of Injective function include:
- The composition of two injective functions is also an injective function.
- If f: A → B and g: B → C are both injective functions, then their composition g(f(x)) is also injective.
- Two sets A and B have the same cardinality if and only if there exists an injective function from A to B and an injective function from B to A.
- If you have a function f: A → B and a subset A’ of A, you can restrict the domain of f to A’ to create a new function. This restricted function is still injective if f is injective on A’.
Graph of Injective Function
One such example of Injective Function is f(x) = x3, and graph the injective function f(x) is provided as below:

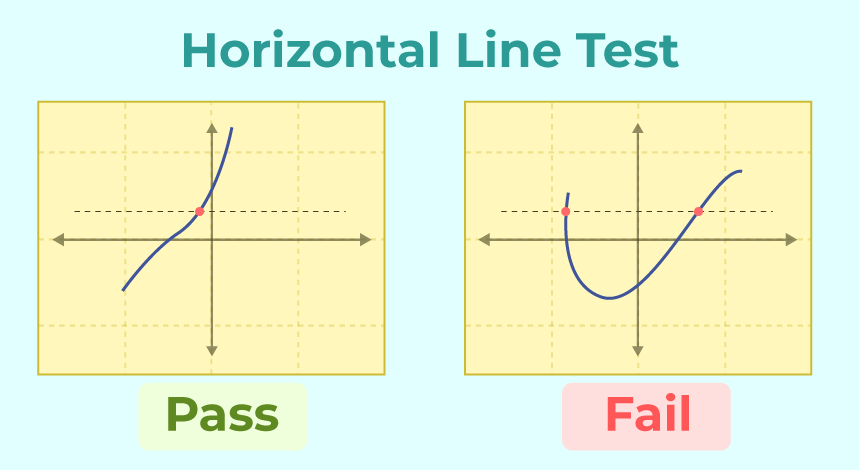
Horizontal Line Test
For any injective function plotted on a coordinate plane, no horizontal line can intersect the graph more than once. In other words, the graph of an injective function never has horizontal line segments that cross it more than once.
Injective, Surjective and Bijective Function
The key differences between Injective, Surjective and Bijective Functions are listed in the following table:
| Property |
Injective Function (One-to-One) |
Surjective Function (Onto) |
Bijective Function (One-to-One and Onto) |
| Definition |
A function where each element in the domain maps to a unique element in the codomain. |
A function where the codomain is completely covered by the elements in the domain. |
A function that is both injective and surjective. |
| Symbol |
f: A ↣ B |
f: A ↠ B |
f: A ⤖ B |
| Unique Mapping |
Each element in the domain maps to a unique element in the codomain. |
Multiple elements in the domain may map to the same element in the codomain. |
Each element in the domain maps to a unique element in the codomain. |
| All Elements in Domain Mapped |
Yes, every element in the domain is mapped to a unique element in the codomain. |
Not necessarily. There may be elements in the codomain with no pre-image in the domain. |
Yes, every element in the domain is mapped to a unique element in the codomain. |
| All Elements in Codomain Covered |
Not necessarily. Some elements in the codomain may not have pre-images in the domain. |
Yes, every element in the codomain has at least one pre-image in the domain. |
Yes, every element in the codomain has exactly one pre-image in the domain. |
| Example |
f(x) = 2x
f: R → R |
f(x) = x2
f: R → R+ |
f(x) = x
f: R → R |
Following illustration shows the difference between all three function:

Read More,
Solved Example on Injective Function
Example 1: Let’s take a simple function, f(x) = 2x. Is this function injective?
Solution:
Yes, f(x) = 2x is indeed an injective function. For every distinct input, you will always get a distinct output.

Example 2: Consider the function f:R→R defined as f(x) = x2. Is this function injective?
Solution:
No, f(x) = x2 is not an injective function because different inputs (e.g., x = 2 and x = -2) can result in the same output (f(2) = 4 and f(-2) = 4).
Example 3: Consider the function f:R→R defined as f(x) = x3. Is this function injective?
Solution:
Yes, f(x) = x3 is an injective function. Every unique input will result in a unique output.
Practice Problems on Injective Function
Problem 1: Determine whether the following function is injective:
- f(x) = 2x + 3
- g(x) = x2 – 4x + 4
- k(x) = ex
- q(x) = x3 + 2x2 – x
- u(x) = 3x – 2
Problem 2: Determine whether the function h(x) = sin x is injective on the interval [0, π]
Problem 3: Consider the function p(x) = 1/x for x ≠ 0: Is p(x) an injective function?
Problem 4: Given the function r(x) = |x|, where x is a real number, is r(x) an injective function?
Problem 5: Consider the function s(x) = √x for x ≥ 0: Is s(x) injective?
Problem 6: Determine whether the function t(x) = cos x is injective on the interval [0, 2π]
Injective Function – FAQs
1. Define Injective Function.
An injective function is a concept where each distinct input corresponds to a different output and no two different inputs yield the same output.
2. Is there another name for an Injective Function?
Yes, injective function is also called one-to-one function.
Read more about One-to-One Function.
3. How Do You Know If a Function is an Injective Function?
To check if a function is injective, ensure that different inputs always produce different outputs.
4. Are all linear functions injective?
No, not all linear functions are injective. It depends on the slope a nonzero slope indicates injectiveness, while a zero slope indicates non-injectiveness.
5. What is the Opposite of an Injective Function?
The opposite of an injective function is a surjective (onto) function, which covers the entire codomain but not the domain.
6. Can a function be both Injective and Surjective?
Yes, a function that is both injective (one-to-one) and surjective (onto) is called bijective.
7. What is the Symbol used to represent an Injective Function?
The symbol often used to represent an injective function is ↦ or ⟼ or ↣.
8. Is the Identity Function Injective?
Yes, the identity function is injective. It maps each element to itself, ensuring that no two distinct elements in the domain map to the same element in the codomain.
|




